1 定义
图是由顶点的有穷非空集合和顶点之间边的集合组成,表示为G(V,E),其中G表示一个图,V是图G中顶点的集合,E是图G中边的集合。
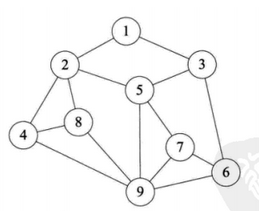
若顶点vi到vj之间的边没有方向,则这条边为无向边,表示为(vi,vj)或(vj,vi),反之为有向边(或弧),表示为<vi,vj>,其中vi称为弧尾,vj称为弧头。若图中所有边都为无向边,则该图为无向图,反之若都为有向边,则为有向图。
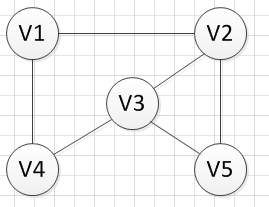
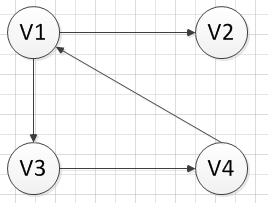
简单图:不存在顶点到其自身的边,且同一条边不重复出现。
无向完全图:任意两个顶点中都存在边的无向图。若顶点为n个,则边数为n(n-1)/2。
有向完全图:任意两个顶点中都存在边的有向图。若顶点为n个,则边数为n(n-1)。
稀疏图和稠密图:有很少条边或弧的图称为稀疏图,反之称为稠密图。
权:与边或弧相关的数;带有权的图称为网
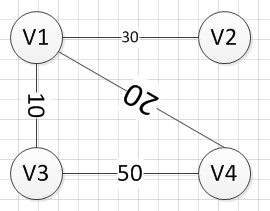
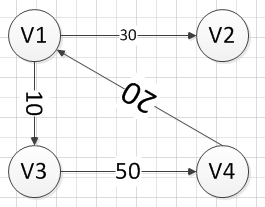
相邻且有边直接连接的两个顶点称为邻接点,列如上图中,V1和V4是邻接点,但V2和V4不是,因为它们之间没有直接相连。在图中,顶点所连边的数目称为度,在有向图中,由于边有方向,则顶点的度分为入度和出度。可以看出,在无向图中,边数是所有顶点度数和的一半,而在有向图中,边数=入度和=出度和。
无向图中,从顶点vi到顶点vj的路径是一个顶点序列,路径的长度为经过的边或弧的数目。第一个顶点和最后一个顶点相同的路径称为回路或环。序列中不出现重复的顶点称为简单路径。,除了第一个顶点和最后一个顶点外,其余顶点不重复的路径称为简单回路。如图,左图为简单回路,而右图不是,因为顶点C出现了2次。

2 连通图
在无向图中,如果两个顶点之间有路径,则称这两个顶点是连通的。如果图中任意两个顶点都是连通的,那么该图为连通图。无向图中的极大连通子图称为连通分量,如图,图2和图3都是图1无向图的连通分量,但图4不是,因为其没有包含极大的顶点数。

在有向图中,如果对于任意两个顶点vi和vj,都存在vi到vj和vj到vi的路径,则称那图为强连通图。在有向图中的极大强连通子图称做有向图的强连通分量。如图左图不是强连通图,因为没有顶点D到顶点A的路径,而右图则是强连通图,其也是左图的强连通分量。

一个连通图的生成树是一个极小连通子图,它含有图中全部n个顶点,但只有n-1条边。在一条生成树中添加一条边,则必然构成一个环,如果减少一条边,则是非连通图。如图图1为连通图,图2和图3都是图1的生成树,但图4不是,因为它不连通。

若一个有向图恰有一个顶点入度为0,其余顶点的入度均为1,则是一棵有向树。一个有向图的生成森林由若干棵有向树组成,含有图中全部顶点,但只有足以构成若干棵不相交的有向树的弧。如图,图2和图3是图1的生成森林。

3 图的抽象数据类型
ADT{
Data
顶点的有穷非空集合和边的集合
Opeartion
CreateGraph(*G,V,VR) //按照顶点集V合边弧集VR定义构造图G
DestroyGraph(*G) //销毁图G
LocateVex(G,u) //返回图G中顶点u的位置,若不存在,则返回其他信息
GetVex(G,v) //返回图G中顶点v的值
PutVex(G,v,value) //将图G中顶点v赋值value
FirstAdjVex(G,*v) //返回顶点v的一个邻接顶点,若无则返回空
NextAdjVex(G,v,w) //顶点w是顶点v的邻接顶点,返回顶点v相对于顶点w的下一个邻接顶点
//若顶点w是顶点v的最后一个邻接顶点,则返回空
InsertVex(*G,v) //在图G种添加顶点v
DeleteVex(*G,v) //删除图G中顶点v及其相关的弧
InsertArc(*G,v,w) //在图G中添加弧<v,w>,如果是无向图,还要添加对称弧<w,v>
DeleteArc(*G,v,w) //在图G中删除弧<v,w>,如果是无向图,还要删除对称弧<w,v>
DFSTraverse(G) //对图G进行深度优先遍历
HFSTraverse(G) //对图G进行广度优先遍历
}