SVM的个人理解

版权声明：本文为博主原创文章，未经博主允许不得转载。 https://blog.csdn.net/asdfgggggggg/article/details/52550674

支持向量机–SVM大家都不会陌生，其实就是一种分类器。在集合空间中寻找一个能够正确分隔这些元素的超平面，当只有两个元素的时候，符合我们条件的超平面有很多，但是找到最佳的超平面的只有一个。在这里面超平面是一条线，是一个wx+b=0的直线。
这里面说一下我遇到的疑惑点：
SMO（Sequential minimal optimization）：参考文献根据pluskid中的博客所提到的，我们使用点到超平面的距离来对集合中的点进行分类。当一个点的margin越大的时候，分隔这个点的效果就越明显，我们也就是去寻找这个距离两侧的点最大的超平面。其中，函数间隔（function margin）。这里面我们假设为1，那么其余的点距离都是大于1的，因为上式可以保证这个函数距离是非负的。但是函数间隔会在超平面不变的情况下，随着w与b的增大而增大，因此在这里我们采用的是几何间隔（geometrical margin），其计算公式可见与函数间隔只是相差一个||w||。从上面可以看出当我们去寻找最佳分类平面的时候，其实就是寻找最大的，在超平面固定的情况下，的值也可以随着 ∥w∥ 的变化而变化。由于我们的目标就是要确定超平面，因此可以把这个无关的变量固定下来，固定的方式有两种：一是固定 ∥w∥ ，当我们找到最优的 时 也就可以随之而固定；二是反过来固定，此时 ∥w∥ 也可以根据最优的 得到。处于方便推导和优化的目的，我们选择第二种，令=1 ，则我们的目标函数化为：当函数距离等于1的时候证明该点在超平面上，这个1是人为进行规定的（为了方便计算），当函数距离大于1的时候证明都在超平面之外。若直线只是在所有数据的一侧，那么这些数据就有小于1的情况，因为数据在函数的同一侧，函数的数值符号是一定的，而分类函数的间隔是+1与-1都会有的，相乘必然会有正负。这种情况是不符合约束条件的，因此超平面分类器必然在两个数据之间。所以取最大的必然会取距离两边点之间的最大距离。因此求出w就可以求出最大的值，但是此时距离由w确定的超平面到最近的点的距离就是。因此可以确定最佳的超平面。
SVM，KKT条件：
有不等式约束的优化问题，可以写为：
min f(x)
s.t g(x)_i>0, i =1,2,3……..n;
h(x)_j=0,j=1.2.3…….m;
求解上述约束条件的最优值，利用lagrange函数将上式写作L(a,b,x) = f(x)+a*g(x)+b*h(x),其中需要满足以下条件：
（1）L(a,b,x)求导为零
（2）h(x) = 0;
（3）a*g(x) =0;
（工优课本上给出了KKT条件，但是当时真心没了解是干什么的，司机硬背之后得到了比较高的成绩，今日的泪水与汗水是当初脑子进的水）
对以上三个条件的讲解：
假设我们的目标函数z=f(x),x为变量向量，随着z的变化，f(x)构成的是一个平面曲面（其中是由一条条等高线构成的），假设约束条件是g(x)=0,那么在坐标系上构成了一条曲线，那么该曲线必然能与f(x)构成的曲面有交点，但是该交点并不是最小的或者最大的，因为在还存在其他的交点，只有在与等高线相切的时候才有可能取得最优值。即等高线和目标函数的曲线在该点的法向量必须有相同方向，所以最优值必须满足：f(x)的梯度 = a* g(x)的梯度，a是常数，表示左右两边同向。这个等式就是L(a,x)对参数求导的结果。

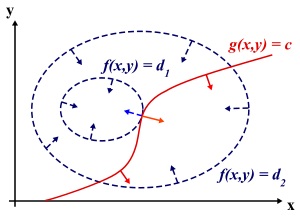
在lagrange构造的函数中，当g(x)符合约束条件的时候可以随着a的变化，取到负无穷，因此通过调整a的值来排除这种情况，可以使用求解p(x)=max{a>=0}L(a,b,x)来规划该值。当g(x)不符合条件或者h(x)！=0的时候，可以调整a或者b使得取值接近正无穷。
因此可以将上式写作：
p(x)={f(x),while x be set some values; unlimit, other x}
因此求解min f(x) = min{x} max{a>0,b>0}L(a,b,x);根据对偶性可以得到上式：max{a>0,b>0} min{x}L(a,b,x)。求解 min{x}L(a,b,x)相当于对L(a,b,x)进行求导。
回归条件：因此需要满足条件1，对于条件2是必然满足的，对于条件3在推导条件1的过程中，需要求解最大值，而a*g(x)<=0的，所以只有在a*g(x)=0的时候符合题意。其中KKT条件只有在求极值向lagrange变换的情况下使用。
在SVM中，KKT条件就是：a(i)(y(i)(w*x(i)+b)-1-s(i))=0与b(i)*s(i)=0 => (C-a(i))*s(i)=0;
(注：s(i)表示松弛变量，C是对松弛变量的容忍度，之所以第二个式子中是C-a(i)，因为b(i)*s(i)>0,而a(i)+b(i)=C在求导的过程中得到的)
可从上面两个式子中得到：
a(i) = 0 => s(i) = 0 => y(i)*(w*x(i)+b) >=1;
a(i) = C => y(i)(w*x(i)+b)-1-s(i)=0 => y(i)(w*x(i)+b)<=1;
0< a(i) < C => s(i) = 0 =>y(i)*(w*x(i)+b)=1
根据上面的公式，判断违背KKT点的条件：
a(i) = 0 => y(i)*(w*x(i)+b) <1;
a(i) = C => y(i)*(w*x(i)+b) >1;
0< a(i) < C =>y(i)*(w*x(i)+b)!=1
然后再不断的更新需要判断的点。
（3）SMO的算法：
1.第一步选取a(i)与a(j)，选取方法是启发式方法；
（这里面是copy过来的：E k =u k -y k ，是根据当前 组合估算的第k个样本的u k 与实际的分类y k 间的差值。启发式选择方法主要思想是每次选择拉格朗日乘子的时候，优先选择样本前面系数 0< a(i) < C 的ai作优化（论文中称为无界样例），因为在界上（ai为0或C）的样例对应的系数ai一般不会更改。启发式搜索方法是选择第一个拉格朗日乘子用的，比如 前面的a2。那么这样选择的话，是否最后会收敛。可幸的是Osuna定理告诉我们只要选择出来的两个ai中有一个违背了KKT条件，那么目标函数在一步迭 代后值会减小。违背KKT条件不代表 0< a(i)< C ，在界上也有可能会违背。是的，因此循环的算法是：（i）在给定初始值ai=0后，先对所有样例进行循环，循环中碰到违背KKT条件的（不管界上还是界内）都进行迭代更新。（ii）第二轮开始就优先针对0< a(i)< C 的样例进行迭代更新，直至此类样例没有ai更新则进入（iii）。（iii）再次对所有样例进行循环一次后再次进入（ii）
（v）循环（ii）（iii）直至迭代终止（达到最大迭代次数或没有ai得到更新）
2.第二部，固定a(i)与a(j)以外的参数，确定W极值条件下的a(i),a(j)用a(i)来进行表示。
在这里注意的是：（1）停止更新的条件是达到了迭代次数或者拉格朗日乘子几乎没有变化（其中这个条件是在循环中建立起来的）。最后收敛的条件是在0< a(i)< C 的样例都遵守kkt条件。（2）求解a(i) 的数值，需要确定a(i) 的范围。（3）其中选取|E(i)-E(i)|值最大，这样收敛速度最快（还需要深入理解）。
文章写得有些杂乱无章。。。因为主要是自己看了好多文章之后自己的疑惑查的答案不断的解析，望见谅！！