最短路径---SPFA算法（C++）

适用范围：给定的图存在负权边，这时类似Dijkstra等算法便没有了用武之地，而Bellman-Ford算法的复杂度又过高，SPFA算法便派上用场了。 我们约定有向加权图G不存在负权回路，即最短路径一定存在。当然，我们可以在执行该算法前做一次拓扑排序，以判断是否存在负权回路，但这不是我们讨论的重点。

算法思想：我们用数组d记录每个结点的最短路径估计值，用邻接表来存储图G。我们采取的方法是动态逼近法：设立一个先进先出的队列用来保存待优化的结点，优化时每次取出队首结点u，并且用u点当前的最短路径估计值对离开u点所指向的结点v进行松弛操作，如果v点的最短路径估计值有所调整，且v点不在当前的队列中，就将v点放入队尾。这样不断从队列中取出结点来进行松弛操作，直至队列空为止

期望的时间复杂度O(ke)， 其中k为所有顶点进队的平均次数，可以证明k一般小于等于2。

实现方法：

　　建立一个队列，初始时队列里只有起始点，再建立一个表格记录起始点到所有点的最短路径（该表格的初始值要赋为极大值，该点到他本身的路径赋为0）。然后执行松弛操作，用队列里有的点作为起始点去刷新到所有点的最短路，如果刷新成功且被刷新点不在队列中则把该点加入到队列最后。重复执行直到队列为空。

判断有无负环：
　　如果某个点进入队列的次数超过N次则存在负环（SPFA无法处理带负环的图）

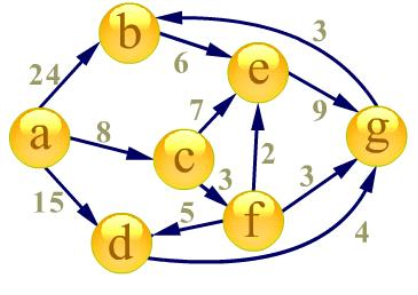
首先建立起始点a到其余各点的
最短路径表格

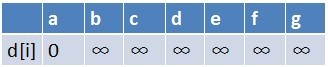
首先源点a入队，当队列非空时：
　１、队首元素（a）出队，对以a为起始点的所有边的终点依次进行松弛操作（此处有b,c,d三个点），此时路径表格状态为：

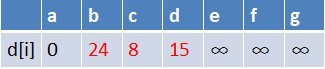
在松弛时三个点的最短路径估值变小了，而这些点队列中都没有出现，这些点
需要入队，此时，队列中新入队了三个结点b,c,d

队首元素b点出队，对以b为起始点的所有边的终点依次进行松弛操作（此处只有e点），此时路径表格状态为：

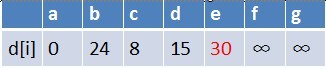
在最短路径表中，e的最短路径估值也变小了，e在队列中不存在，因此e也要
入队，此时队列中的元素为c，d，e

队首元素c点出队，对以c为起始点的所有边的终点依次进行松弛操作（此处有e,f两个点），此时路径表格状态为：

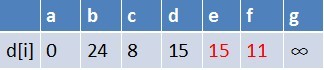
在最短路径表中，e，f的最短路径估值变小了，e在队列中存在，f不存在。因此
e不用入队了，f要入队，此时队列中的元素为d，e，f

 队首元素d点出队，对以d为起始点的所有边的终点依次进行松弛操作（此处只有g这个点），此时路径表格状态为：

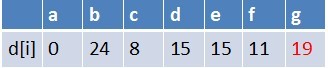
在最短路径表中，g的最短路径估值没有变小（松弛不成功），没有新结点入队，队列中元素为f，g

队首元素f点出队，对以f为起始点的所有边的终点依次进行松弛操作（此处有d，e，g三个点），此时路径表格状态为：

在最短路径表中，e，g的最短路径估值又变小，队列中无e点，e入队，队列中存在g这个点，g不用入队，此时队列中元素为g，e

队首元素g点出队，对以g为起始点的所有边的终点依次进行松弛操作（此处只有b点），此时路径表格状态为：

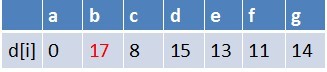
在最短路径表中，b的最短路径估值又变小，队列中无b点，b入队，此时队列中元素为e，b
队首元素e点出队，对以e为起始点的所有边的终点依次进行松弛操作（此处只有g这个点），此时路径表格状态为：

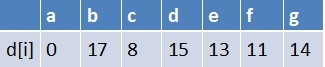
在最短路径表中，g的最短路径估值没变化（松弛不成功），此时队列中元素为b

队首元素b点出队，对以b为起始点的所有边的终点依次进行松弛操作（此处只有e这个点），此时路径表格状态为：

在最短路径表中，e的最短路径估值没变化（松弛不成功），此时队列为空了

最终a到g的最短路径为１４

代码：

spfa.h

#ifndef SPFA_H
#define SPFA_H

#pragma once

#include<iostream>
#include<string>
#include<queue>
using namespace std;

/*
本算法是使用SPFA来求解图的单源最短路径问题
采用了邻接表作为图的存储结构
可以应用于任何无环的图
*/

struct ArcNode
{
    int adjvex;     // 尾端的顶点下标
    ArcNode *next;  // 下一条边的尾端顶点
    int weight;
};

struct Vnode
{
    string data;   // 顶点信息
    ArcNode *firstarc;  // 第一条依附在该顶点的边
};

struct Dis
{
    string path;  // 从源点到该顶点的最短路径
    int weight;   // 最短路径的权重
};

class Graph
{
private:
    int vexnum;  // 点的个数
    int edge;    // 边的个数
    Vnode *node; // 邻接表
    Dis *dis;    // 记录最短路径信息的数组
public:
    Graph(int vexnum, int edge);
    ~Graph();
    void CreateGraph(int kind);
    bool check_edge_value(int start, int end);
    void print();
    bool SPFA(int begin);
    void print_path(int begin);
};



#endif // SPFA_H

spfa.cpp

#include "spfa.h"

Graph::Graph(int vexnum, int edge) {
    //对顶点个数和边的条数进行赋值
    this->vexnum = vexnum;
    this->edge = edge;

    //为邻接矩阵开辟空间
    node = new Vnode[this->vexnum];
    dis = new Dis[this->vexnum];
    int i;
    //对邻接表进行初始化
    for (i = 0; i < this->vexnum; ++i) {
        node[i].data = "v" + to_string(i + 1);
        node[i].firstarc = NULL;
    }
}

Graph::~Graph() {
    int i;
    //释放空间，但是记住图中每个结点的链表也要一一释放
    ArcNode *p, *q;
    for (i = 0; i < this->vexnum; ++i) {
        //一定要注意这里，要判断该顶点的出度到底是否为空，不然会出错
        if (this->node[i].firstarc) {
            p = node[i].firstarc;
            while (p) {
                q = p->next;
                delete p;
                p = q;
            }
        }

    }
    delete [] node;
    delete [] dis;
}

// 判断我们每次输入的的边的信息是否合法
//顶点从1开始编号
bool Graph::check_edge_value(int start, int end) {
    if (start<1 || end<1 || start>vexnum || end>vexnum) {
        return false;
    }
    return true;
}

void Graph::print() {
    cout << "图的邻接表的打印：" << endl;
    int i;
    ArcNode *temp;
    //遍历真个邻接表
    for (i = 0; i < this->vexnum; ++i) {
        cout << node[i].data << " ";
        temp = node[i].firstarc;
        while (temp) {
            cout << "<"
                << node[i].data
                << ","
                << node[temp->adjvex].data
                << ">="
                << temp->weight
                << " ";
            temp = temp->next;
        }
        cout << "^" << endl;
    }
}

void Graph::CreateGraph(int kind)
{
    //kind代表图的种类，2为无向图
    cout << "输入边的起点和终点以及各边的权重(顶点编号从1开始)：" << endl;
    int i;
    int start;
    int end;
    int weight;
    for (i = 0; i < this->edge; ++i)
    {
        cin >> start >> end >> weight;
        //判断输入的边是否合法
        while (!this->check_edge_value(start, end)) {
            cout << "输入边的信息不合法，请重新输入：" << endl;
            cin >> start >> end >> weight;
        }
        ArcNode *temp = new ArcNode;
        temp->adjvex = end - 1;
        temp->weight = weight;
        temp->next = nullptr;
        //如果该顶点依附的边为空，则从以第一个开始
        if (node[start-1].firstarc == nullptr)
        {
            node[start-1].firstarc = temp;
        }
        else
        {
            //否则，则插入到该链表的最后一个位置
            ArcNode *now = node[start - 1].firstarc;
            //找到链表的最后一个结点
            while (now->next)
            {
                now = now->next;
            }
            now->next = temp;
        }

         //如果是无向图，则反向也要添加新的结点
        if (kind == 2)
        {
            //新建一个新的表结点
            ArcNode *temp_end = new ArcNode;
            temp_end->adjvex = start - 1;
            temp_end->weight = weight;
            temp_end->next = nullptr;
            //如果该顶点依附的边为空，则从以第一个开始
            if (node[end - 1].firstarc == nullptr)
            {
                node[end - 1].firstarc = temp_end;
            }
            else
            {
                //否则，则插入到该链表的最后一个位置
                ArcNode *now = node[end - 1].firstarc;
                //找到链表的最后一个结点
                while (now->next)
                {
                    now = now->next;
                }
                now->next = temp_end;
            }
        }
    }
}

bool Graph::SPFA(int begin)
{
    bool *visit;
    //visit用于记录是否在队列中
    visit = new bool[this->vexnum];
    int *input_queue_time;
    //input_queue_time用于记录某个顶点入队列的次数
    //如果某个入队列的次数大于顶点数vexnum，那么说明这个图有环，
    //没有最短路径，可以退出了
    input_queue_time = new int[this->vexnum];
    queue<int> s;  //队列，用于记录最短路径被改变的点

    /*
    各种变量的初始化
    */
    int i;
    for (i = 0; i < this->vexnum; ++i)
    {
        visit[i] = false;
        input_queue_time[i] = 0;
        //路径开始都初始化为直接路径,长度都设置为无穷大
        dis[i].path = this->node[begin - 1].data + "-->" + this->node[i].data;
        dis[i].weight = INT_MAX;
    }

    //首先是起点入队列，我们记住那个起点代表的是顶点编号，从1开始的
    s.push(begin - 1);
    visit[begin - 1] = true;
    ++input_queue_time[begin - 1];

    dis[begin - 1].path = this->node[begin - 1].data;
    dis[begin - 1].weight = 0;

    int temp;
    ArcNode *temp_node;
    // 进入队列的循环
    while (!s.empty())
    {
        //取出队首的元素，并且把队首元素出队列
        temp = s.front();
        s.pop();

        //必须要保证第一个结点不为空（为了避免出现"人为选择了非法结点-1这种情况"）
        if (node[temp].firstarc)
        {
            temp_node = node[temp].firstarc;
            while (temp_node)
            {
                //如果边<temp,temp_node>的权重加上temp这个点的最短路径
                //小于之前temp_node的最短路径的长度，则更新
                //temp_node的最短路径的信息
                if (dis[temp_node->adjvex].weight > (temp_node->weight + dis[temp].weight))
                {
                    //更新dis数组的信息
                    dis[temp_node->adjvex].weight = temp_node->weight + dis[temp].weight;
                    dis[temp_node->adjvex].path = dis[temp].path + "-->" + node[temp_node->adjvex].data;
                    //如果还没在队列中，加入队列，修改对应的信息
                    if (!visit[temp_node->adjvex])
                    {
                        visit[temp_node->adjvex] = true;
                        ++input_queue_time[temp_node->adjvex];
                        s.push(temp_node->adjvex);
                        if (input_queue_time[temp_node->adjvex] > this->vexnum)
                        {
                            cout << "图中有负环" << endl;
                            return false;
                        }
                    }
                }
                temp_node = temp_node->next;
            }
            visit[temp] = false;
        }
    }
    return true;
}


void Graph::print_path(int begin)
{
    cout << "以顶点" << this->node[begin - 1].data
        << "为起点，到各个顶点的最短路径的信息：" << endl;
    int i;
    for (i = 0; i < this->vexnum; ++i) {
        if (dis[i].weight == INT_MAX) {
            cout << this->node[begin - 1].data << "---" << this->node[i].data
                 << "  无最短路径，这两个顶点不连通"
                 << endl;
        }
        else
        {
            cout << this->node[begin - 1].data << "---" << this->node[i].data
                 << "  weight: " << dis[i].weight
                 << "  path: " << dis[i].path
                 << endl;
        }
    }
}

main.cpp

#include"spfa.h"

//检验输入边数和顶点数的值是否有效，可以自己推算为啥：
//顶点数和边数的关系是：((Vexnum*(Vexnum - 1)) / 2) < edge
bool check(int Vexnum, int edge) {
    if (Vexnum <= 0 || edge <= 0 || ((Vexnum*(Vexnum - 1)) / 2) < edge)
        return false;
    return true;
}
int main() {
    int vexnum; int edge;
    cout << "输入图的种类：1代表有向图，2代表无向图" << endl;
    int kind;
    cin >> kind;
    //判读输入的kind是否合法
    while (1) {
        if (kind == 1 || kind == 2) {
            break;
        }
        else {
            cout << "输入的图的种类编号不合法，请重新输入：1代表有向图，2代表无向图" << endl;
            cin >> kind;
        }
    }

    cout << "输入图的顶点个数和边的条数：" << endl;
    cin >> vexnum >> edge;
    while (!check(vexnum, edge)) {
        cout << "输入的数值不合法，请重新输入" << endl;
        cin >> vexnum >> edge;
    }


    /*------正文------*/
    Graph graph(vexnum, edge);
    graph.CreateGraph(kind);
    graph.print();
    //记得SPFA一个参数，代表起点，这个起点从1开始
    if (graph.SPFA(1))
    {
        graph.print_path(1);
    }
    return 0;
}

运行结果：

1.检测正环：

2.检测负环：

注：

SPFA算法相当于在Bellman-Ford算法的基础上，对选边策略做了优化，采用类似BFS的遍历顺序对边进行relax操作，从源点处开始扩散，从而提高算法的效率。

参考资料：

http://lib.csdn.net/article/datastructure/10344

https://blog.csdn.net/qq_35644234/article/details/61614581

参考资料2代码中存在的问题：

• SPFA函数中，visit数组没有重置成false，以及res变量定义但没使用
• main函数需要判断是否有负环，再进行路径打印
• SPFA可以对负权值的图进行操作，所以check_edge_value可以不传weight形参