PCA主成分分析之三维演示(Matlab)
写这个的主要原因是实验课上的要求,原本需要写一个演示 PCA 原理的 demo ,按照实验指导书上来说,在二维上演示就好了,但是为了折腾和无聊装逼,我写了这个程序,我觉得更能直观的看出 PCA 的原理。可以完整的看到数据从三维降到二维,再到一维的整个过程。别看是简简单单的感觉,要写出来,还是需要对原理有比较深刻的认识的,代码没有参照网上,仅靠个人推导和联想,多多指教。
目录
原理简介
主成分分析(principal component analysis PCA),通过正交变换将一组可能存在相关性的变量转换成一组线性不相关的变量,转换之后的这组变量叫做主成分。常用于提取数据主要特征变量,常用于高维数据的降维。在用统计分析的方法研究多变量的时候,变量的个数太多,增加了复杂性,由于变量之间是有一定的相关性的,也就是说不同的变量所代表的全局信息是有重叠,有冗余的。其算法流程如下图所示:
结果展示
如图1所示绘制随机的3维点,如图2所示,选取特征值最大的两个特征向量进行投影,绘制其投影平面,如图3所示,绘制出3维到2维的投影垂线以示意这个过程的原理。如图4所示为最后投影得到的二维点在三维坐标中的位置,可以看到,这些点都位于一个平面上,如图5所示为二维点到一维点的投影线,所选的投影基为特征值最大的特征向量,如图6所示,绘制了二维到一维的投影垂线,如图7所示为二维降为一维的点。整个过程演示了一个三维特逐渐降为一维的过程,特征有所损失,但是仍能被区分。
 图1 随机三维点
图1 随机三维点
|
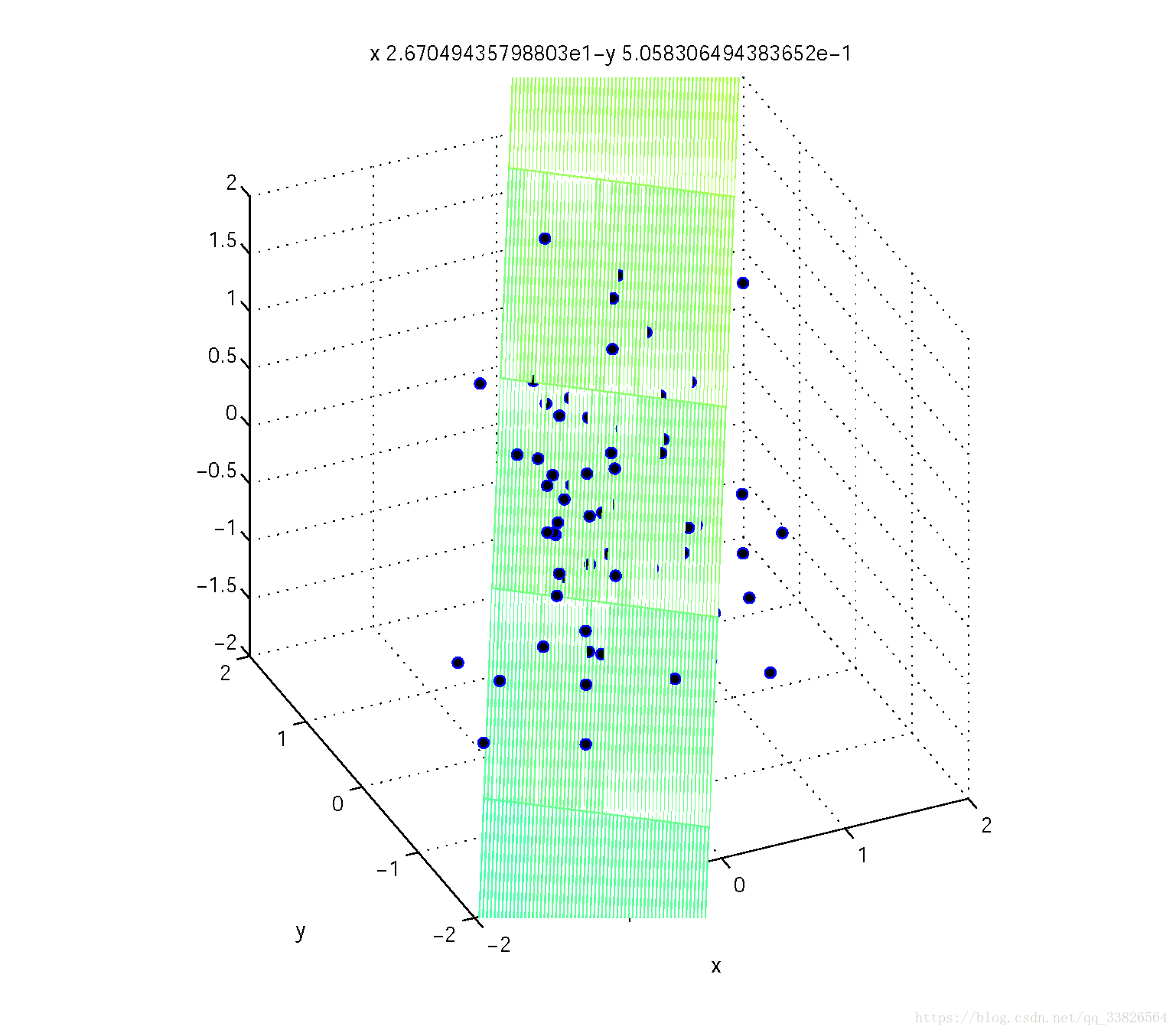 图2 三维到二维投影面
图2 三维到二维投影面
|
 图3 三维到二维的投影过程 图3 三维到二维的投影过程
|
 图4 三维到二维的投影点 图4 三维到二维的投影点
|
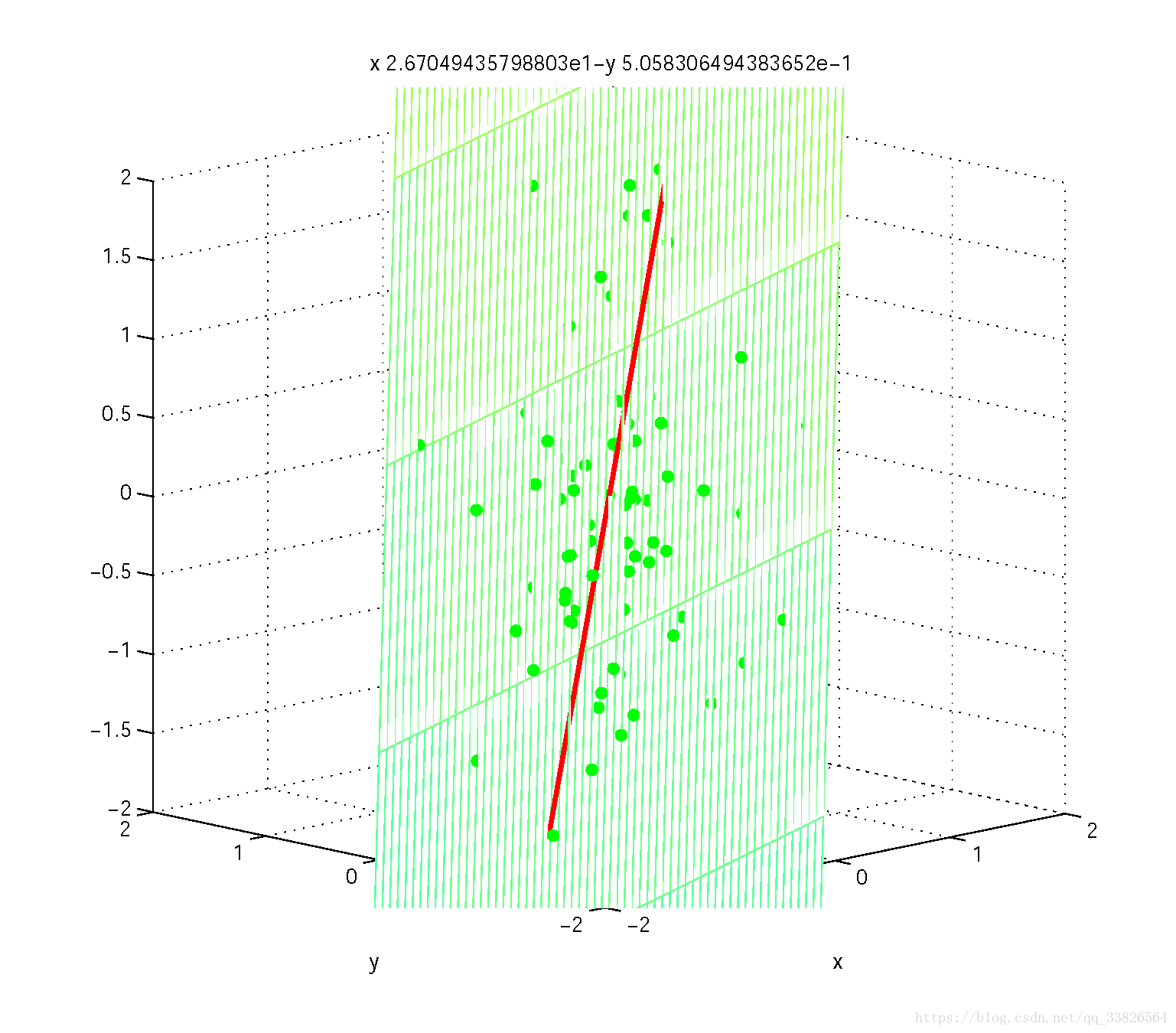 图5 二维到一维的投影线 图5 二维到一维的投影线
|
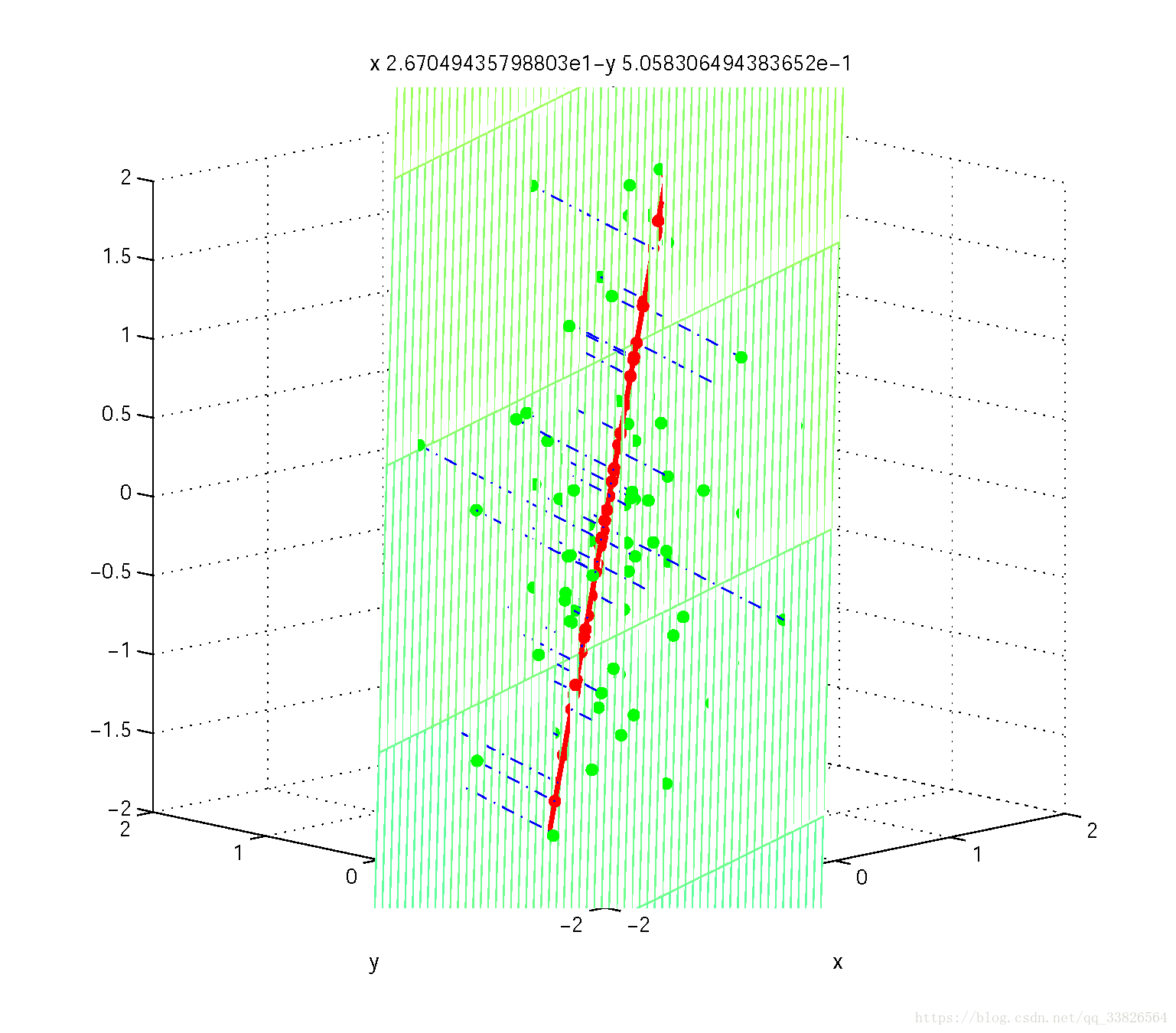 图6 二维到一维的投影过程 图6 二维到一维的投影过程
|
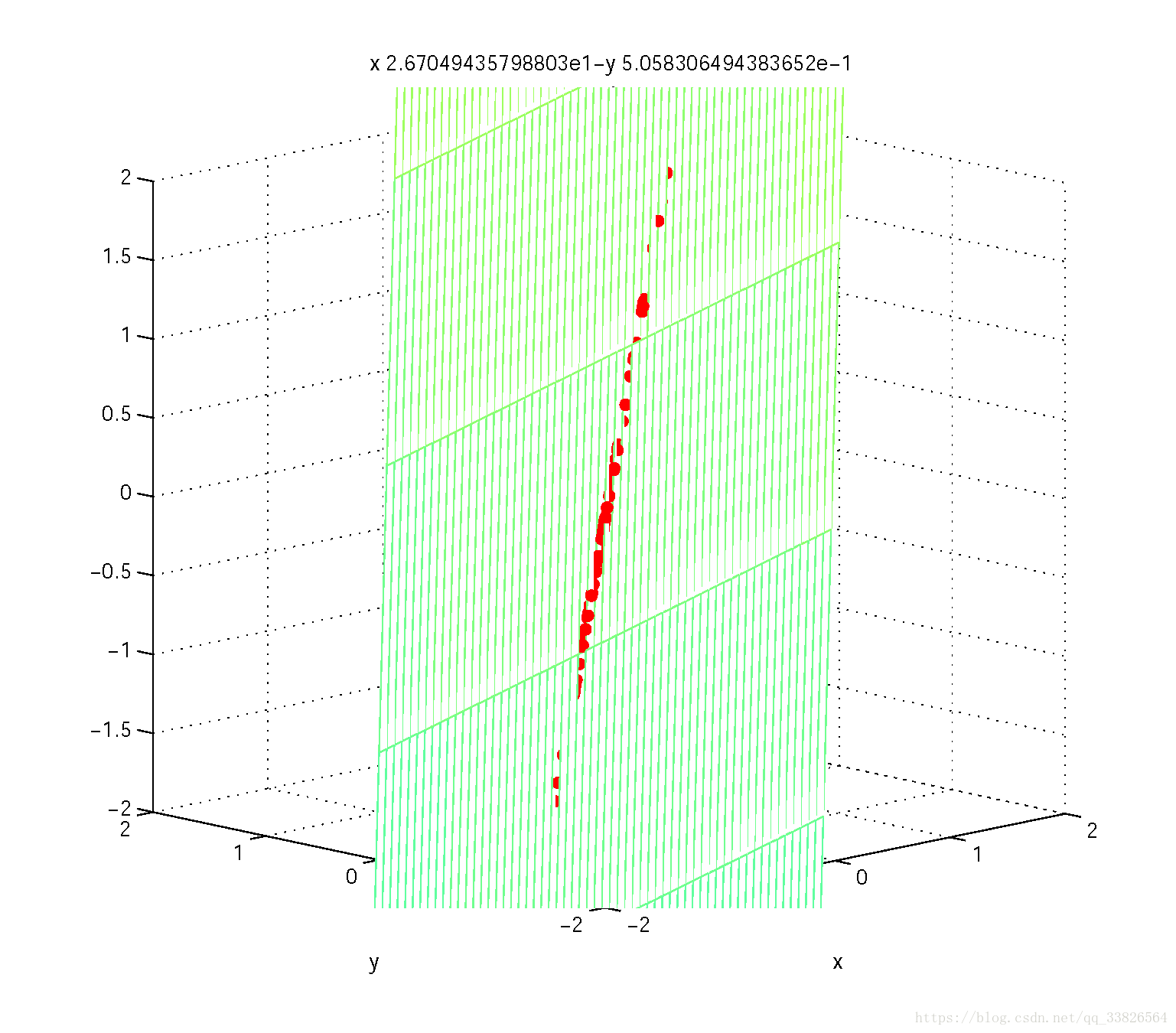 图7 二维到一维的投影点 图7 二维到一维的投影点
|
源代码
function PCAdemo
close all;clear;clc;
h_figure = figure;
mu = [0 0 0];
%协方差矩阵,对角为方差值0.3,0.35
dim = 3;
var = [0.2 0 0; 0 0.5 0; 0 0 0.8];
samNum = 100;
data = mvnrnd(mu,var,samNum);
h_plotMain = plot3(gca,data(:,1),data(:,2),data(:,3),'o',...
'MarkerSize',5,'MarkerFaceColor','k');
xlim([-2 2]);ylim([-2 2]);zlim([-2 2]);
grid on;axis square;hold on;
pause();
covdata = cov(data);%求协方差矩阵
[eigVector, eigValue] = eig(covdata);%求协方差矩阵的特征值和特征向量
eigValue = diag(eigValue)';
[eigValue_sort, IX] = sort(eigValue, 2, 'descend');
eigVector_sort = [];
for i = 1:dim
tempIX = IX(i);
eigVector_sort = [eigVector_sort eigVector(:, tempIX)];
end
base_3to2 = eigVector_sort(:,1:2);%三维降2维
base_3to1 = eigVector_sort(:,1);%三维降1维
base_3to2 = base_3to2';
base_3to1 = base_3to1';
%%%%%绘制3维变成2维度的投影平面%%%%%
A = base_3to2(1, :);%新基i帽(相对原基)
B = base_3to2(2, :);%新基j帽(相对原基)
C = [0 0 0];
syms x y z;
D = [ones(4, 1), [[x, y, z]; A; B; C]];%由空间解析几何的内容知道D的行列式等于零就是平面方程。
detd = det(D);
z = solve(detd,z);
ezmesh(z,[-2, 2, -2, 2]);
pause();
%%%%%%%%%%%%
data_proj3_2 = base_3to2*data';%投影到新基坐标(相对新基)
data_proj3_1 = base_3to1*data';%投影到新基坐标(相对新基)
data_proj3_2 = data_proj3_2';
data_proj3_1 = data_proj3_1';
data_proj_respect_to_orienbasis3_2 = [];%新基坐标用原基表示
data_proj_respect_to_orienbasis3_1 = [];%新基坐标用原基表示
for i = 1:samNum
data_proj_respect_to_orienbasis3_2 = [data_proj_respect_to_orienbasis3_2;...
data_proj3_2(i,1)*base_3to2(1,:)+data_proj3_2(i,2)*base_3to2(2,:)];
data_proj_respect_to_orienbasis3_1 = [data_proj_respect_to_orienbasis3_1;...
data_proj3_1(i)*base_3to1(1,:)];
end
%绘制3维降为2维后的数据
h_plot3_2 = plot3(gca,data_proj_respect_to_orienbasis3_2(:,1),...
data_proj_respect_to_orienbasis3_2(:,2),data_proj_respect_to_orienbasis3_2(:,3),...
'o','MarkerSize',5,'MarkerEdgeColor','g','MarkerFaceColor','g');
%绘制3维降为2的投影虚线
hl3_2 = [];
hl3_1 = [];
for i = 1:samNum
dd = [data_proj_respect_to_orienbasis3_2(i,:);data(i,:)];
hl3_2(i) = plot3(gca,dd(:,1),dd(:,2),dd(:,3),'-.','markersize',10);
end
pause();
delete(h_plotMain);delete(hl3_2);
pause();
%绘制3维降为1的基准线
h_zhixian = plot3(gca,data_proj_respect_to_orienbasis3_1(:,1),...
data_proj_respect_to_orienbasis3_1(:,2),data_proj_respect_to_orienbasis3_1(:,3),...
'color','r','linewidth',2);
pause();
%绘制3维降为1的数据
h_plot3_1 = plot3(gca,data_proj_respect_to_orienbasis3_1(:,1),...
data_proj_respect_to_orienbasis3_1(:,2),data_proj_respect_to_orienbasis3_1(:,3),...
'o','MarkerSize',5,'MarkerEdgeColor','r','MarkerFaceColor','r');
%绘制3维降为1的投影虚线
for i = 1:samNum
dd=[data_proj_respect_to_orienbasis3_1(i,:);data_proj_respect_to_orienbasis3_2(i,:)];
hl3_1(i)=plot3(gca,dd(:,1),dd(:,2),dd(:,3),'-.','markersize',10);
end
pause();
delete(h_plot3_2);
delete(hl3_1);
delete(h_zhixian);
end 可以直接复制以上代码,或者可以下载链接:https://download.csdn.net/download/qq_33826564/10574325
GitHub: https://github.com/swq123459/PCA-3D-demo
体会
1.使用PCA对数据进行降维的思路:将输入的样本看成一个随机向量,即
有M个样本,说明发生了M次 事件, 有N维,每一维为单独的随机变量 ,若要将降维,降维后的需满足其内部各维之间的协方差为0,已保证降维后的数据无冗余,每一位表示的信息不正交不重叠;同时各维的方差需要最大,因为方差大代表着数据集中性越差,说明越方便被辨别。随机向量协方差矩阵中,各维均值位于对角线,协方差位于其他非对角线位置,我们需要对角线值最大,其他位置值为0,这不免让我们想到了矩阵的对角化。对角化完成的功能真是将矩阵除对角线为其他元素变成0.矩阵的对角化表达式为
其中A为待对角化矩阵,T为A的特征向量组成的矩阵,这里我们将A看成是的协方差矩阵,那么T就是这个协方差矩阵特征向量组成的矩阵。对角化的过程已经完成了协方差0的任务,接下来使各维的方差最大,即B的对角线元素最大。因为特征值大的特征向量是矩阵变换的主要方向,所以其占的变换成分应该比较大,对B的对角线元素影响也比较大,所以这里才有根据特征值来排序特征向量来组成矩阵T的方法。按照成分的贡献率,可以执行降维,维度贡献率不能少于 。
在计算协方差矩阵的时候,A为样本数据集矩阵,N为样本维数,需要注意的是样本数据集A必须去均值,即使样本各维均值为0,这样使用该公式计算出来的才是协方差矩阵。
在执行数据降维的时候,从二维数据降至一维的变换为A,得到的这个一维的数据是以A的基为基的坐标再乘以这个基的范数,若这个变换本身就同其基一致的话,得到的一维数据为其投影长度。Matlab中计算特征向量的函数已经完成了特征向量单位化的操作,所以,将数据同其内积得到的便是投影长度。实验中涉及将这个投影长度在原来的维度中显示的问题,只要将这个投影长度乘以原来投影的基向量就行了。
Matlab中如果要在上写文中索引当前axes,进行绘图, 只需要进行一次hold on,就可以防止plot句柄的自动回收。
