KMP是指Donald Knuth、 Vaughan Pratt和James H. Morris三个算法牛人的合并简称，Donald Knuth就是那个写《计算机程序设计艺术》的ACM图灵奖得主。这个算法是在线性时间复杂度下完成字符串匹配任务，这个算法太牛逼了，简洁优美但十分太晦涩，充满技巧性，给大神跪了。
问题定义：
字符串匹配问题：在文本串S中寻找模式串W（单词串）的位置。对应程序语言就是：在（文本）字符数组中S[]中寻找模式字符数组W[]的起始索引m。
暴力解法：
很容易想到一个朴素解法，算法复杂度为O(mn),就是遍历整个文本字符串，检查每个字符与模式串的首字符是否相同，如果相同则继续比对模式串后面的字母，直到所有模式串字母比对完，如果遇到不匹配则跳出循环从模式串首字母开始从头检验。代码参考链接https://blog.csdn.net/To_be_to_thought/article/details/84679263
基本概念：
的前缀是子串
，
，且
，我们就说
开始于
的后缀是子串
，
，且
，我们就说结束于
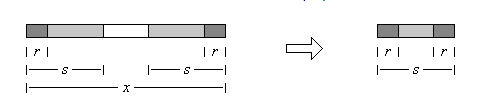
这里的前缀和后缀是严格前缀和严格后缀，不包括原字符串本身。字符串的边缘串(a border of x)是x的一个子串r，且
)，也就是说x的边缘串既是x的前缀串，又是x的后缀串，并且b是边缘的长度。
例如：
表示空串。
则x的边缘串有
，边缘串
长度为0，边缘串
长度为2。空串总是字符串x的边缘串，空串没有边缘串。在预处理阶段，模式串的每个前缀串的最长边缘的长度是确定的。
重要定理：r和s都是字符串x的边缘串，并且r的长度小于s，则r也是s的边缘串。
因此
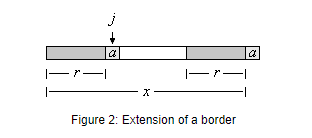
x为字符串，a是字母表里的一个字符，如果ra也是xa的边缘串，x的一个边缘串r可以通过a（一个字符）延伸。
下面举个例子做做匹配实验：
文本串S: ABC ABCDAB ABCDABCDABDE
模式串W: ABCDABD
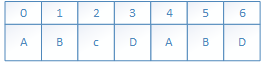
前三次比对如图：
按照朴素的思想应该进行如下调整再比对：
再转到下一步：
但因为已经比对过S[8]和S[9]的信息，可以利用这个信息直接将新的比对任务的起点移到如下图：
当S[10]和W[2]发生失配时，直接将新的比对任务移动到S[11]，下图：
当S[17]和W[6]发生失配时，直接将新的比对任务移动到S[15]，如下图：
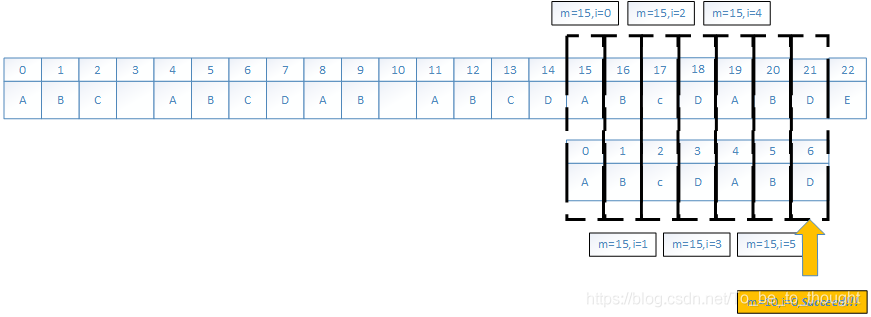
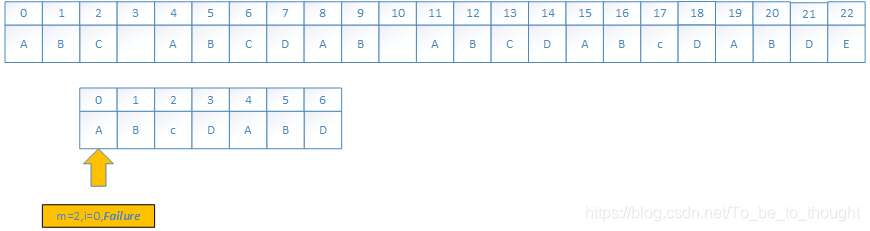
按照以时间换空间的思想，应该在失配时将字符串的信息记录下来，下面来看看next数组到底存的是什么信息？
我们现在假设存在部分匹配表（partial match table）数组T[]，这个表用于告诉我们：当前匹配失败时如何寻找预匹配起点。如果有一个以S[m]为起点(S[m+k-1])的比对任务在S[m+i]和W[i]失配时，下一个可能的比对任务可能以S[m+i-T[i]]为起点，尤其是下一个可能的位置一定在比m大的索引上（因为T[i]<i），并且我们不需要检验S[m+i-T[i]]到S[m+i-1]的字符串是否相等，因为T[i]表明：在模式串中W[0：i-1]组成的子串的前缀和后缀最长公共串长度为T[i]。
举个例子：
下面把这个例子构造部分匹配表的算法流程描述一下（如图）：
| i |
j |
j |
… |
… |
i |
j |
b[i] |
| 0 |
-1 |
|
|
|
0 |
|
-1 |
| 0 |
-1 |
|
|
|
1 |
0 |
0 |
| 1 |
0 |
-1 |
|
|
2 |
0 |
0 |
| 2 |
0 |
|
|
|
3 |
1 |
1 |
| 3 |
1 |
|
|
|
4 |
2 |
2 |
| 4 |
2 |
|
|
|
5 |
3 |
3 |
| 5 |
3 |
1 |
0 |
|
6 |
1 |
1 |
算法开始 :i=0,j=-1,b[i=0]=-1
i=0<6,(j=-1<0不符合内循环条件) j=0,i=1,b[i=1]=j=0
i=1< 6,(j = 0, p[i] != p[j]) j = b[0] = -1 (j=-1<0跳出循环) i=2 , j=0 b[2]=j=0
i=2<6 ( j=0>=0 , p[2]=p[0] 跳出循环) i=3,j=1,b[3]=j=1
i=3<6, (j=1,p[i=3]=p[j=1]跳出循环) i=4 , j=2 , b[i=4]=j=2
i=4<6 , (j=2>=0, p[i=4]=p[j=2] 跳出循环) i= 5, j=3, b[i=5]=j= 3
i=5<6 (j=3>=0,p[i=5]=!p[j=3] ) j=b[j=3]=1 (j=1>=0,p[i=5]!=p[j=1] ) j=b[j=1]=0 (j=0>=0,p[i=5]=p[j=0]跳出循环) i=6, j=1 , b[i=6]=1
i=6结束循环
在进行运算时我们发现这个b[i=0]=-1的-1设置的恰到好处，会比b[0]=0好很多！！！
下篇敬请期待！！！
参考文献：
https://en.wikipedia.org/wiki/Knuth%E2%80%93Morris%E2%80%93Pratt_algorithm
http://www.inf.fh-flensburg.de/lang/algorithmen/pattern/kmpen.htm