版权声明:本文为博主原创文章,未经博主允许不得转载。 https://blog.csdn.net/firstchange/article/details/84582777
算法导论在本章为我们展开了算法的画卷,介绍了几种基础的算法,并深化了其中的思想,让我们一起来看看。
插入排序
首先来看问题的描述:
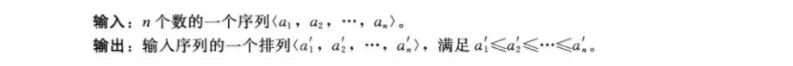
我在代码大全里介绍过隐喻,现在在把它拿来再合适不过了。我们可以把插入排序看着是扑克牌,ok这样就好理解多了。
假设桌子上有几张牌{ 3, 9, 6, 10, K, J, 5}(我们忽略花色),现在我们要打牌,我们需要将牌进行排序,我们会这样做:
- 先抓一张3
- 再抓一张9,比较一下9 > 3,把牌插在3后面
- 再抓一张6,比较一下6 > 3且6 < 9,我们把牌插在3和9直接
- 重复执行
ok,我们就很容易地实现了一个插入排序的过程,其实很多算法就是在我们生活中,只是我们没有很好地去归纳。而且通过隐喻的方式去理解复杂,抽象的概念是非常有效的。我们再来理解一下书上的伪代码

第一行可以理解为牌堆里的牌,接下来把当前的牌存入临时变量中,i表示最后一张牌的顺序(一般打牌都是升序的)。那么while中的就相当于做比较的过程,思考究竟应该把牌插哪儿,假设我们很笨,一次只能看一张牌,我们从最后一张牌开始看。如果待插牌比较大,那就不要继续比较了,直接插在最后就行,如果待插牌比较小,我们就再往前进行比较,并且把相对大的牌往后移(这里和实际还是有些区别的,事实上我们插牌时并不会一个个后移)。按照这样依次抓牌,到最后我们手里的牌就是有序的了。
ok伪代码就如此搞定了,不难吧。
下面我们要用严格的数学来证明算法是正确的。
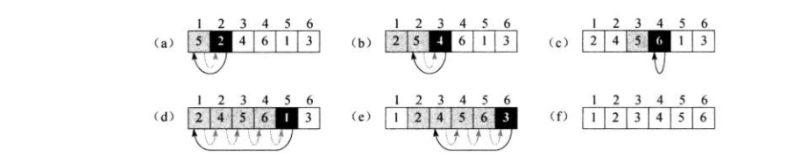
例子中是将序列{5, 2, 4, 6, 1, 3}进行排序。
证明的关键在于循环不等式:
- 初始化:循环的第一次迭代之前,为真
- 保持:如果循环的某次迭代之前为真,则下次迭代之前依然为真
- 终止:在终止时,不等式为我们提供一个有用的性质,有助于证明算法是正确的
这类似于数学归纳法,为了证明某条性质成立,需要证明一个基本情况和一个归纳步。初始化为基本情况,保持则为归纳步。
ok,我们来看详细的证明过程:

如此插入排序算法的正确性就得以保证了。
小结
- 通过隐喻来理解复杂抽象的概念是非常有效的
- 算法的设计是需要通过严格的数学证明的