SMO算法理解

SMO算法看了近3遍感觉还是有点朦朦胧胧，模模糊糊。

所以索性，理解多少写多少，避免遗忘。可能会有很多错误，欢迎指正。

主要基于李航的《统计学习方法》

SMO(sequential minimal optimization)序列最小最优化算法

我们在讨论支持向量机的学习问题时，可以将其转换成求解凸二次规划问题。实现支持向量机的学习是要找到这样的凸二次规划问题的全局最优解，SMO就是支持向量机学习的一种快速算法，也是一种启发式算法。

基本思路：

如果所有变量的解都满足此优化问题的KKT条件，那么这个最优化问题的解就得到了。(KKT条件是该最优化问题的充分必要条件)。否则，选择两个变量，固定其他变量，针对这两个变量构建一个二次规划问题。子问题的两个变量，一个是违反KKT条件最严重的那一个，另一个由约束条件自动确定。如此，SMO算法将原问题不断分解为子问题求解，进而达到求解原问题的目的。[1]

特点：

将原始的二次规划问题分解为只含有两个变量的二次规划子问题，对子问题不断求解，使得所有的变量满足KKT条件

包含两部分：

1、求解两个变量二次规划的解析方法

2、选择变量的启发式方法

SMO算法要解的是如下凸二次规划的对偶问题：

其中，K( ，)是核函数

两个变量二次规划的求解方法

1、SMO的最优化问题的子问题

前面提到将原始的二次规划问题分解为只含有两个变量的二次规划子问题，所以假设选定两个变量 $\alpha_{1}$ 、 $\alpha _{2}$ ，其他变量相当于常数，省略常数后，SMO的最优化问题的子问题可以化简成以下形式：

最终的优化目标是：

………… (1)

原来的约束条件变成：

s.t. $\alpha _{1}y_{1}+\alpha _{2}y_{2}=-\sum_{i=3}^{N}\alpha _{i}y_{i}=\xi$ （用 $\xi$ 表示）…………(*)

还有 $0\leq \alpha _{i}\leq C$

（注意，对于式子 $\alpha _{1}y_{1}+\alpha _{2}y_{2}=-\sum_{i=3}^{N}\alpha _{i}y_{i}=\xi$ ，我们在用 $\alpha _{1}$ 表示 $\alpha _{2}$ 时，等式两边同时乘 $y _{1}$ 就可以，不要用除以 $y _{1}$ 的方式，要时刻记住 $y _{1}^{^{2}}$ =1）

2、视为一元函数，求导取极值

(1)式可以看成是一个二元函数，根据于 $\alpha _{1}$ 和 $\alpha _{2}$ 的约束关系，可以把 $\alpha _{1}$ 消去。不过我们的目的是为了关于 $\alpha _{2}$ 求导，导数为0的点就是要找的极值点，所以这里既可以把 $\alpha _{1}$ 消去后对 $\alpha _{2}$ 求导，也可以直接在现在这个式子上对 $\alpha _{2}$ 求导。

根据(*)式得

…………(2)

代入(1)式中，可以看成是一个一元函数

用 $w(\alpha _{1},\alpha _{2})$ 来表示最优化的目标，将 $\alpha _{1}=(\xi -y_{2}\alpha _{2})y_{1}$ 带入得到

$w(\alpha _{2})=\frac{1}{2}K_{11}(\xi -\alpha _{2}y_{2})^{2}+\frac{1}{2}K_{22}\alpha _{2}^{2}+y_{2}K_{12}(\xi -\alpha _{2}y_{2})\alpha _{2}-(\xi -\alpha _{2}y_{2})y_{1}-\alpha _{2}+v_{1}(\xi -\alpha _{2}y_{2})+y_{2}v_{2}\alpha _{2}$

对上式中的 $\alpha _{2}$ 求导等于0

…………(3)

借用参考3中博客解析

把(4)(6)(7)式带入到(3)式中去，并进行化简

其中 $\eta =K_{11}+K_{22}-2K_{12}$

得到 $\alpha _{2}^{new,unc}=\alpha _{2}^{old}+\frac{y_{2}(E_{1}-E_{2})}{\eta }$ …………(8)

3、对原始解进行裁剪

裁剪的问题，博客2里得部分讲的很详细(具体的就不贴出来，请参看最后的参考博文链接)

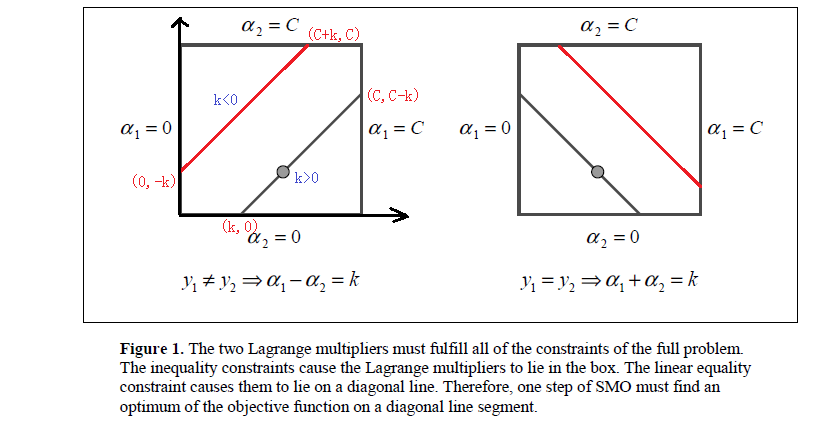
对约束条件对应的*式 $\alpha _{1}y_{1}+\alpha _{2}y_{2}=\xi$ ，考虑两种情况，分别如上图所示。

$\alpha _{2}^{new}$ 需要满足约束条件 $0\leq \alpha _{i}\leq C$ ，所以最优值 $\alpha _{2}^{new}$ 的取值范围也要满足条件 $L\leqslant \alpha _{2}^{new}\leqslant H$

L和H分别是 $\alpha _{2}^{new}$ 坐在的对角线段端点的界。

当 $y_{1}\neq y_{2}$ 时， $\alpha _{2}$ 的可行域为 $\left [max(0,\alpha _{1}-\alpha _{2}), \right min(C,C-\alpha _{1}+\alpha _{2})]$ ，区间端点分别为：

$L=max(0,\alpha _{2}^{old}-\alpha _{1}^{old})$ ， $H=min(C,C+\alpha _{2}^{old}-\alpha _{1}^{old})$

当 $y_{1}= y_{2}$ 时， $\alpha _{2}$ 的可行域为 $\left [max(0,\alpha _{1}+\alpha _{2}-C), \right min(C,\alpha _{1}+\alpha _{2})]$ ，区间端点分别为：

$L=max(0,\alpha _{2}^{old}+\alpha _{1}^{old}-C)$ ， $H=min(C,\alpha _{2}^{old}+\alpha _{1}^{old})$

所以在更新 $\alpha _{2}$ 时，要先求出 $\alpha _{2}$ 的可行域，然后用之前的那个公式求出极值点 $\alpha _{2}$ ，然后看极值点 $\alpha _{2}$ 处的在不在可行域范围内，在的话就使用极值点处的 $\alpha _{2}$ ，不在的话就使用边界值H或者L更新，具体更新规则为：