普里姆算法—Prim算法
算法思路:
从已选顶点所关联的未选边中找出权重最小的边,并且生成树不存在环。
其中,已选顶点是构成最小生成树的结点,未选边是不属于生成树中的边。
(普里姆算法与求最短路径的迪杰斯塔拉算法思想很类似)
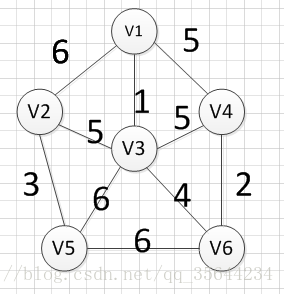
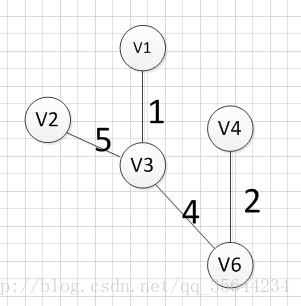
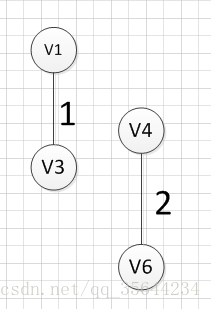
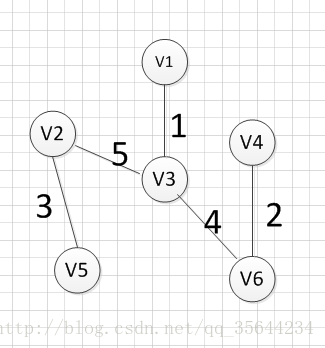
下面我们对下面这幅图求其最小生成树:
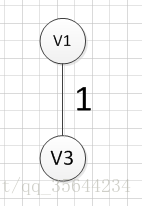
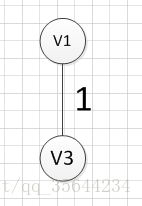
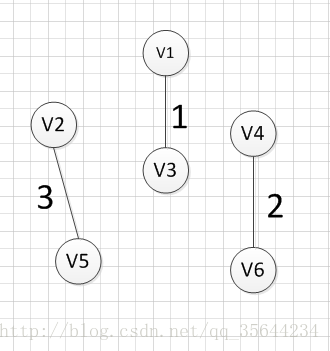
假设我们从顶点v1开始,所以我们可以发现(v1,v3)边的权重最小,所以第一个输出的边就是:v1—v3=1:
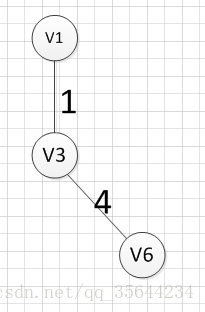
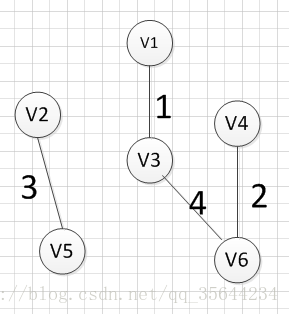
然后,我们要从v1和v3作为起点的边中寻找权重最小的边,首先了(v1,v3)已经访问过了,所以我们从其他边中寻找,发现(v3,v6)这条边最小,所以输出边就是:v3—-v6=4
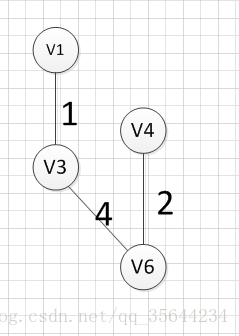
然后,我们要从v1、v3、v6这三个点相关联的边中寻找一条权重最小的边,我们可以发现边(v6,v4)权重最小,所以输出边就是:v6—-v4=2.
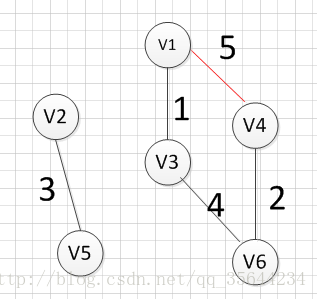
然后,我们就从v1、v3、v6、v4这四个顶点相关联的边中寻找权重最小的边,发现边(v3,v2)的权重最小,所以输出边:v3—–v2=5
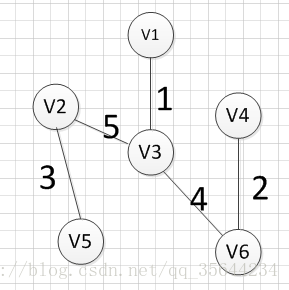
然后,我们就从v1、v3、v6、v4,v2这2五个顶点相关联的边中寻找权重最小的边,发现边(v2,v5)的权重最小,所以输出边:v2—–v5=3
最后,我们发现六个点都已经加入到集合U了,我们的最小生成树建立完成。
克鲁斯卡算法
算法思路:
(1)将边按权值从小到大的顺序添加到新图中,保证添加的过程中不会形成环
(2)重复上一步直到连接所有顶点,此时就生成了最小生成树。这是一种贪心策略。
将图中所有边按照权重的大小 从小到大一个一个按顺序组合成最小生成树,在组合过程新加入的边会导致生成树形成环,那这条边就舍弃,直到所有顶点都添加到生成树中为止。
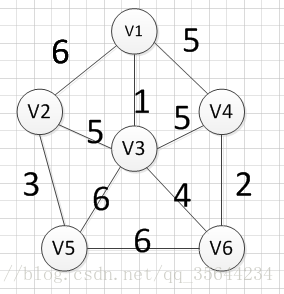
这里同样我们给出一个和Prim算法讲解中同样的例子,模拟克鲁斯卡算法生成最小生成树的详细的过程:
首先完整的图如下图:
然后,我们需要从这些边中找出权重最小的那条边,可以发现边(v1,v3)这条边的权重是最小的,所以我们输出边:v1—-v3=1
然后,我们需要在剩余的边中,再次寻找一条权重最小的边,可以发现边(v4,v6)这条边的权重最小,所以输出边:v4—v6=2
然后,我们再次从剩余边中寻找权重最小的边,发现边(v2,v5)的权重最小,所以可以输出边:v2—-v5=3,
然后,我们使用同样的方式找出了权重最小的边:(v3,v6),所以我们输出边:v3—-v6=4
好了,现在我们还需要找出最后一条边就可以构造出一颗最小生成树,但是这个时候我们有三个选择:(v1,V4),(v2,v3),(v3,v4),这三条边的权重都是5,首先我们如果选(v1,v4)的话,得到的图如下:
我们发现,这肯定是不符合我们算法要求的,因为它出现了一个环,所以我们再使用第二个(v2,v3)试试,得到图形如下:
我们发现,这个图中没有环出现,而且把所有的顶点都加入到了这颗树上了,所以(v2,v3)就是我们所需要的边,所以最后一个输出的边就是:v2—-v3=5
OK,到这里,我们已经把克鲁斯卡算法过了一遍
---------------------
转载自:https://blog.csdn.net/qq_35644234/article/details/59106779?utm_source=copy