机器学习 --- 线性支持向量机

支持向量机是一种二分类模型，目的是寻找一个超平面对样本进行划分，其基本模型定义为特征空间上的间隔最大的线性分类器。

一、线性支持向量机的直观理解

给定训练样本集 $D=\{ (x_{1},y_{1}),(x_{2},y_{2}),...,(x_{m},y_{m}) \}$ ， $y_{i} =\{-1, +1 \}$ ，模型旨在能基于训练集在样本空间中找到一个合适的划分超平面。

在下图的二维平面中，希望有一个超平面即一条线可以将正负样本很好分开：

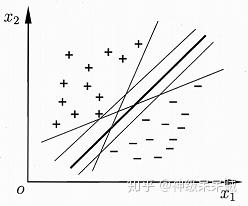
由上图直观的感受，可以将样本分开的划分超平面可能会有很多，但一般会选择中间那条黑色加粗的线。毕竟训练集从某种程度上来说只是近似于样本分布，因此更希望能找到一个划分超平面对分类结果具有很好的鲁棒性，即具有对训练集中没有包含的某些样本具有很好的泛化效果。而中间的这条线对分类的结果有着更好的“容忍性”

二、线性超平面

在样本空间中，划分超平面定义成：

$w^{T}x+b=0$

根据线性代数的知识，参数 $w$ 决定了超平面的方向，又被称作法向量，参数 $b$ 决定了超平面与远点之间的距离。这与逻辑回归中假设函数十分的相像。不同之处在于，逻辑回归中通过激活函数将函数值映射到 $(0,1)$ 区间上。但实质上决定分类结果的还是参数 $w$ ， $b$

类似地，假设超平面 $(w,b)$ 能将训练样本正确分类，则满足：

$\left\{ \begin{aligned} & w^{T}x_{i}+b \geq +1 & y_{i}=+1 \\ & w^{T}x_{i}+b\leq -1 & y_{i}=-1 \\ \end{aligned} \right.$

由之前的逻辑回归可以知道，当点能满足：

$\left\{ \begin{aligned} & w^{T}x_{i}+b > 0 & y_{i}=+1 \\ & w^{T}x_{i}+b < 0 & y_{i}=-1 \\ \end{aligned} \right.$

也能分类样本，但这种情况下当 $(w,b)$ 同时放大或缩小，结果不受影响。超平面还是那个超平面，即多个满足一定规则的 $(w,b)$ ，其可能对应同一个超平面。

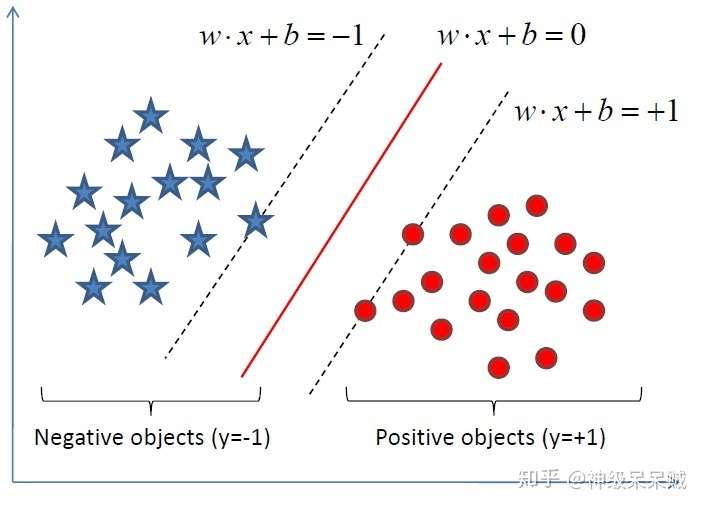
三、支持向量

上图中，距离超平面最近的几个训练样本点使得下式成立

$y_{i}(w^{T}x_{i}+b)=1 \qquad \qquad (1)$

则这些点又被称作支持向量，两个异类支持向量到超平面的距离 $\gamma$ 称作间隔。

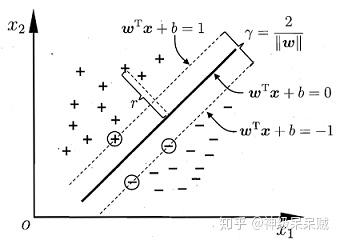
由高中数学，这个间隔等于两个异类支持向量的差在 $w$ 上的投影。因此：

$\gamma=\frac{(\overrightarrow{x_{+}}-\overrightarrow{x_{-}})\overrightarrow w^{T}}{\vert \vert w\vert\vert} \qquad \qquad(2)$

联立(1)(2)式，得到：

$\gamma=\frac{2}{\left| \left| w \right| \right|}$

整个问题现在归类到最大间隔 $\gamma$ ，最小化 $\frac{1}{\gamma}$ ，由此列出约束方程：

$\min \limits_{w,b} \ \frac{1}{2} \left| \left| w \right| \right| \qquad\qquad\qquad\qquad\qquad(3)$

$s.t \quad y_{i}(w^{T}x_{i}+b)\geq1$

这就是支持向量机的基本型式。

四、求解向量机基本型式

问题转化成如何求解(3)式，由于这是一个凸二次规划问题，我们使用拉格朗日乘子法将问题转化成对偶问题（拉格朗日原理请参照拉格朗日乘子法和KTT条件）。对每个约束条件添加拉格朗日乘子 $\alpha_{i}\geq0$ ，去掉约束条件，目标函数写成：

$L(w,b,\alpha)=\frac{1}{2}\left| \left| x \right| \right|^{2}+\sum_{i=1}^{m}{\alpha_{i}(1-y_{i}(w^{T}x_{i}+b))} \qquad \qquad (4)$

然后固定 $\alpha$ ，如果要让 $L$ 关于 $w,b$ 最小化，对 $w,b$ 分别求偏导：

$\frac{\partial L}{\partial w}=0\Rightarrow w=\sum_{i=1}^{m}{\alpha_{i}y_{i}x_{i}} \qquad\qquad\qquad(5)$

$\frac{\partial L}{\partial b}=0\Rightarrow \sum_{i=1}^{m}{\alpha_{i}y_{i}}=0 \qquad\qquad\qquad(6)$

将(5)(6)代入(4)中，得到对偶式：

$\max \limits_{\alpha} \ \sum_{i=1}^{m}{\alpha_{i}}-\frac{1}{2}\sum_{i=1}^{m}{\sum_{j=1}^{m}{\alpha_{i}\alpha_{j}y_{i}y_{j}x^{T}_{i}x_{j}}} \qquad \qquad (7)$

$s.t \ \ \ \ \sum_{i=1}^{m}{a_{i}y_{i}}=0 \ \ \ \ \ \ \ \ \qquad \qquad(8)$

$\ \quad \ \ \ \ \ a_{i}\geq0$

求解上式用到了SMO算法:

算法思路是首先固定 $a_{i}$ 之外的所有参数，再求 $a_{i}$ 的极值。约束项 $\sum_{i=1}^{m}{a_{i}y_{i}}=0$ 保证了 $a_{i}$ 能通过其他的变量导出。于是SMO算法每次选择两个变量 $a_{i},a_{j}$ ，固定其他参数，迭代至收敛。

主要的步骤是：

选取一对需要更新的变量 $a_{i},a_{j}$
固定 $a_{i},a_{j}$ 以外的参数，求解(7)式获得更新后的 $a_{i},a_{j}$

求解过程中，在仅考虑 $a_{i},a_{j}$ 的情况下，约束条件(8)可以重写为：

$\alpha_{i}y_{i}+\alpha_{j}y_{j}+\sum_{k\ne i,j}^{}{a_{k}y_{k}}=0 \qquad a_{i}\geq 0,a_{j}\geq 0 \ \ \ \ \ \ \ \ \ \ \ (9)$

代入到(7)式中，消去 $\alpha_{j}$ ，得到一个关于 $\alpha_{i}$ 的单变量二次规划问题。

求出 $\alpha$ 的值后，由(5)式求解参数 $w$ :

$w^{*}=\sum_{i=1}^{m}{\alpha_{i}y_{i}x_{i}}$

这里的 $w^{*}$ 指得是极值情况下的 $w$ 值，对应于边界的支持向量，再求参数 $b$ ：

$y(w^{T}x+b)=1$

即：

$\left\{ \begin{aligned} & \max \limits_{y_{i}=-1}w^{T}x_{i}+b=-1 \\ & \min \limits_{y_{i}=1}w^{T}x_{i}+b=1 \\ \end{aligned} \right.$

那么极值情况下的 $b^{*}$ :

$b^{*}=\frac{1}{2}[\max \limits_{y_{i}=-1}w^{*T}x_{i}+\min \limits_{y_{i}=1}w^{*T}x_{i}]$

成功求解参数 $w,b$ 后，划分超平面也就确立下来。

1.支持向量机通俗导论（理解SVM的三层境界） - Mac Track - CSDN博客

2.拉格朗日对偶问题（Lagrange duality）

3.深入理解拉格朗日乘子法（Lagrange Multiplier) 和KKT条件

4.周志华. 机器学习[M]. 清华大学出版社, 2016