MATLAB方程式求解

分享一下我老师大神的人工智能教程！零基础，通俗易懂！http://blog.csdn.net/jiangjunshow

也欢迎大家转载本篇文章。分享知识，造福人民，实现我们中华民族伟大复兴！

第十章聯立方程式解

解聯立方程式為線性代數之第一步，MATLAB 在這方面具有強大的解題功能。利用矩陣除法可以在解題技術上發揮相當大的功效。在工程上，一般線性聯立方程式常用作結構分析或機構設計，計算桁架之應力等。其他如化學程序中之質能平衡、電子學中之電路分析等等均可利用線性方程式得解。在前述之二維繪圖指令中，部份可配合統計上的需要加以應用，對於某些資料之說明甚有幫助。有關線性聯立方程式解題之指令可以參考：

inv(A) ：矩陣Ａ之反矩陣，又稱為，Ａ需為方矩陣
det(A) ：矩陣Ａ之行列式值，Ａ需為方矩陣
Ｘ=pinv(A) ：虛擬反矩陣，Ｘ為與A'同大小之矩陣，且A*X*A=A及X*A*X=X
rank(A) ：矩陣Ａ之階數
X=inv(A)*C ：使用反矩陣求AX=C之解
X=A/C ：使用左除法求AX=C之解
X=D/C ：使用右除法求XＣ=Ｄ之解
B=rref(A) ：簡化方程式型式

10.1 線性矩陣應用指令

線性代數以矩陣表示，會有諸多特殊名稱，在應用上相當普遍，有必要進行瞭解。有些部份在前面之說明中業已經提到，但在這裡則特別另加說明。

行列式與反矩陣

在工程數學或線性代數中，行列式與反矩陣是常用的矩陣特性。尤其在討論聯立方程式之解的過程中更常用到。反矩陣有如一個矩陣的倒數，一個方矩陣若為Ａ，則其反矩陣可以A ^-1表示，而其與原矩陣之關係為：


AA^-1=I   A^-1A=I

其中，Ｉ稱為單位矩陣(Identity matrix)，其大小為方矩陣，而對角線元素值均為1。在MATLAB中有一個指令稱為eye，可以用以建立這種單位矩陣。例如：


eye(4)
ans =
  1     0     0     0
  0     1     0     0
  0     0     1     0
  0     0     0     1

矩陣Ａ之反矩陣以inv(A)表示，有如一個數之倒數一樣。例如，設Ａ為一魔術方陣magic(4)：


A=rand(4)

A =
 0.9355    0.0579    0.1389    0.2722
 0.9169    0.3529    0.2028    0.1988
 0.4103    0.8132    0.1987    0.0153
 0.8936    0.0099    0.6038    0.7468

其反矩陣即為inv(A)表示，其結果設為Ｂ，則：


B=inv(A)
B =
-1.5054    3.6825   -1.4860   -0.4013
 5.3255   -7.0376    3.9063   -0.1473
-20.0637   22.9531   -8.5486    1.3769
17.9531  -22.8718    8.6384    0.7080

根據定義，原矩陣與其反矩陣相乘應等於單位矩陣，且相乘之順序不拘，亦即：Ａ*B與B*A均應等於Ｉ：


B*A
ans =
 1.0000    0.0000    0.0000   -0.0000
 0.0000    1.0000   -0.0000    0.0000
-0.0000    0.0000    1.0000   -0.0000
-0.0000    0.0000   -0.0000    1.0000

上述結果即為單位矩陣，可以試試以A*B，其結果應相同。此處Ａ、Ｂ及Ｉ均為方矩陣，且Ａ矩陣之行列式值或det(A)需不得為零，否則其反矩陣不能存在。此種矩陣不存在的情形，稱為奇異矩陣(singular)。一個矩陣若具奇異特性，則其行列值為零，例如：


D=magic(4)

D =
 16     2     3    13
  5    11    10     8
  9     7     6    12
  4    14    15     1

d=det(D)
d =     0

行值式之值為零，表示其反矩陣不存在，故即使用inv(D)指令也會產生一些數字，但其結果並不可靠，而且會有一些警告訊息出現，例如：


dd=inv(D)

Warning: Matrix is close to singular or badly scaled.
      Results may be inaccurate. RCOND = 1.306145e-017.
dd =
1.0e+014 *
 0.9382    2.8147   -2.8147   -0.9382
 2.8147    8.4442   -8.4442   -2.8147
-2.8147   -8.4442    8.4442    2.8147
-0.9382   -2.8147    2.8147    0.9382

上述結果之值也變成很大，顯然不是正確的值。不信的話可以用 AA^-1=I， A^-1A=I 印證一下（在此至少證實一下「垃圾進拉圾出(Gabage in, gabage out」這句名言）。

所以，某矩陣是否為奇異矩陣，可以使用det進行檢驗。其值若為零則屬奇異矩陣。

特徵值及特徵向量(Eigen Value & Eigen Vector)

線性代數中，最重要的工具是利用特徵值與特徵向量（Eigenvalues & Eigenvectors）來說明方矩陣之多項式特性，此兩者均為方型矩陣。利用矩陣之操作，可以作出相等效果之矩陣等式，但型式更為簡化，或容易得解。設特徵矩陣值與特徵向量其分別為D與V，則其與原矩陣Ａ之關係如下：


A * V= V * D

假設有一個方矩陣Ａ係由亂數函數產生，其Ｖ與Ｄ可以利用eig(Ａ)指令如下求得：


A=rand(3);
[V, D]= eig(A)

A =
 0.4103    0.3529    0.1389
 0.8936    0.8132    0.2028
 0.0579    0.0099    0.1987
V =
 0.4053    0.6812    0.0680
 0.9136   -0.7124   -0.4004
 0.0319   -0.1688    0.9138
D =
 1.2167         0         0
      0    0.0068         0
      0         0    0.1987
A*V

ans =
 0.4931    0.0046    0.0135
 1.1116   -0.0048   -0.0796
 0.0388   -0.0011    0.1816
V*D

ans =
 0.4931    0.0046    0.0135
 1.1116   -0.0048   -0.0796
 0.0388   -0.0011    0.1816

由上述的演算，得知A*Ｖ及Ｖ*Ｄ是一樣的。eig()之指令尚有另外一種型式，即：


[V,D] = eig(A,B)

其中，ＡＢ分別為兩矩陣，Ｄ為對角矩陣特徵值，而Ｖ為對應之特徵向量。其關係如下：


 A * V = B * V * D

其使用範圍可以參考線性代數的內容。

所謂線性方程式係指方程式中之變數僅屬一階者，其幕次不能大於一，且任何項中不得有兩變數相乘或相除之情形。在矩陣表示法上，通常採用[A][x]=[b]之型式，其解為[x]=[A]/[b]或[x]=[b]/[A]。

對於線性聯立方程式目前已經發展出許多種解法，其中包括變數迭代消去法及克雷蒙法(Creamer's Method)。目前MATLAB 所使用之解法則以變數迭代消去法為主，或稱為高斯(Gauss Ｅlimination)消去法。這是利用兩線性方程式分別乘以某特定常數，使其與另一方程式之同一變數係數相同，因而兩式相減得以消除該變數。如此展轉消除，最後可以得聯立方程之解。茲舉例說明如下：


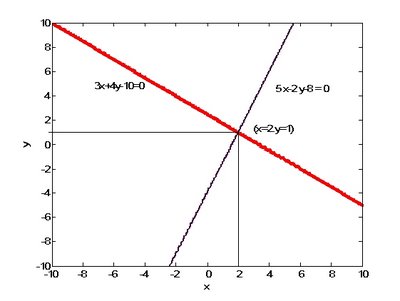
  3x +4y =10
  5x -2y =8

上述聯立方程式中，先將第一式乘兩邊5、第二次兩邊乘3，兩式相減，即可得：


   5(4y) - 3(-2y) = 5* 10 - 3*8

由上式整理之後，可得果為y = 1；代入原式任一式可得x = 2，終得解。如果利用第九章之繪圖指令可以繪出此兩條曲線，由其交點即可得到相同的解。


   ezplot('3*x+4*y-10',[-10,10]);hold on 
   ezplot('5*x-2*y-8',[-10,10])

圖10.1

利用這樣的解法並不是解線性方程式之重點，因為線性代數方程式可用矩陣的型式表示，甚至以矩陣之乘除法可以得解。以上面之聯立線性方程式為例，可以化成ＡＸ＝Ｃ之型式，設x=x1，y=x2：

左除法求解

利用MATLAB求解時，只要用矩陣倒除即可，或稱為左除法。例如一組聯立方程式以矩陣表示為[A][X]=[C]時，其未知數項[X]可以利用MATLAB倒除的指令求得，即[X]＝[A]/[C]：


A=[3 4;5 -2];
C=[10;8];
X=A/C 

X =
    2
    1

結果立即得到x1=2、x2=1。

反矩陣法求解

解上式矩陣有時可用反矩陣法。反矩陣有倒數的意義，但在矩陣中必須為方矩陣，且須為非特異矩陣(non-singular)。通常用( ^-1)次方表示之，如A ^-1 。其基本特質為與原矩陣相乘後，將得到單位矩陣Ｉ：


  A^-1A=AA^-1=I

以此乘於ＡＸ＝Ｃ之兩側，可得：


  A^-1AX=A^-1C 　或A^-1AX=IX=X= A^-1C

在MATLAB反矩陣A ^-1 之求法為inv(A)；Ｉ或稱為單位矩陣，表示為eye(A)。就上面之聯立方程式之解，可以用MATLAB演算如下：


A=[3 4;5 -2];
C=[10;8];
X=inv(A)*C 
X =
   2.0000
   1.0000

所得的結果與前述之分析相同。理論上雖然如此，在演算時求反矩陣較費時間，使用左除法是
為較佳的操作法。

範例：有一組聯立方程式如下：


   6x - 3y +5z = 12
  10x + 4y -8z =-20
  -6x + 2y +3z = 15

解：先安排Ａ及Ｃ矩陣，再利用左除法求得[X]。


A=[6 -3 5;10 4 -8;-6 2 3];C=[12 -20 15]';
x=A/C
C=A*x 

x =
   0.0479
   2.1737
   3.6467
C =
  12.0000
 -20.0000
  15.0000

由上述的計算，可以迅速得到結果，即　x= 0.0479, y= 2.1737, z= 3.6467。通常利用MATLAB解聯立方程式，亦會碰到無解的情形，此時或稱為特異狀況（或 |A| 為零的情形）。前述之左除結果，可用以反求Ｃ值，Ｃ＝Ａx，其結果也正確。

10.2 範例一：桁架負重分析

範例一：有一重物Ｗ架在天花板之ＡＢ兩點上，其剛性支架ＡＣ與ＢＣ與點Ｃ處以梢聯結並由此吊掛重物。支架ＡＣ與ＢＣ與天花板間之角度分別為a₁與b₂。試求其間受力之關係。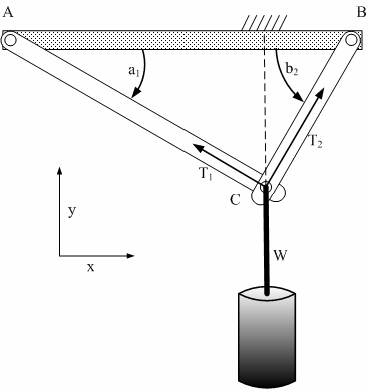

解：

設支架ＡＣ與ＢＣ上之支撐力分別為T1、T2，則依直角座標分析，其作用在點Ｃ之X與Y方向力的關係如下：


x方向:　　T₁cos(a₁)-T₂cos(b₂)=0
y方向:　　T₁sin(a₁)+T₂sin(b₂)=W

以矩陣表示，其AT=W之型式如下：

　　
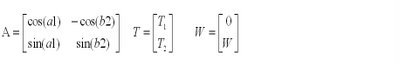
因此，由T=A/W之左除法可以得到答案。其相關程式如下：


function [T1,T2]=findT(a1,b2,W)
% Program to find tensions in supports
% Inputs:
%    a1,b2:inclined angles, in degrees
%        W:weight, in kg
% Ouputs:T:tensions in supports, kg
% Example: T=findT(30,60,100)
A=[cosd(a1) -cosd(b2); sind(a1) sind(b2)];
W=[0 W]';
T=A/W;T1=T(1);T2=T(2);

執行例：

設夾角a1=30度, b2=60度, W=100公斤，求張力T1及T2。
>> [T1,T2]=findT(30,60,100)
T1 =           50
T2 =       86.603

得到AC、BC桿上之張力分別為50公斤與86.603公斤。

10.2 範例二：電路分析

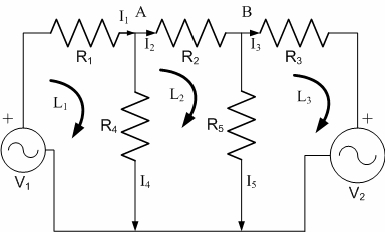
範例二：有一電路如下圖，試寫一MATLAB程式，求解各電阻器上之電流。

圖3.電路圖

就克希荷夫(Kirchhoff)定律，可以在電路上任選定三個迴圈建立電阻與電壓降三項聯立方程式，及電流經Ａ、Ｂ兩點分流時建立之二項聯立方程式，其結果如下：

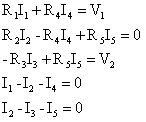
整理此組聯立方程式，其變數Ｉ有五項，其方程式有五組，故應可得解。茲以矩陣[R][I]=[V]表示，利用左除法即為[I]=[R]/[V]。其各變數矩陣分別為：

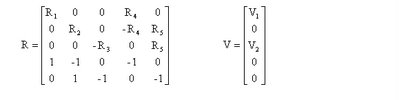
程式內容：


function Current=findC(v1,v2,r)
% Prog using Kirchhoff's law to find the currents in a circuit.
% Inputs:
%   v1, v2: Voltage of generators. volts
%   r: the elements of resistances in Kohms. r=[r1 r2 r3 r4 r5]
% Outputs:
%   current: currents through resistors [c1 c2 c3 c4 c5], in ma.
% Example: current=findC(100,50,[5 100 200 150 250])
V=[v1 0 v2 0 0]';
R=[r(1) 0 0 r(4) 0;0 r(2) 0 -r(4) r(5);0 0 -r(3) 0 r(5);...
　　　1 -1 0 -1 0;0 1 -1 0 -1];
Current=R/V;

執行例：設v1=100V，v2=75V，R=[80 120 250 150 200] KΩ，其電流之安培數(ma)分別如下：


>> current=findC(100,75,[80 120 250 150 200])
current =
       0.5082
       0.1126
      -0.1166
       0.3956
       0.2292

這是分別在各分路上之電流值，其中有負號者表示與原先設定之方向相反。

10.2 範例三：穀倉通風系統分析

範例三：

圖４.穀倉通風系統

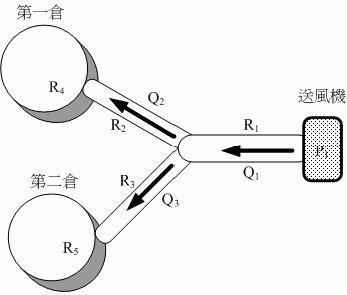
某一組穀倉乾燥系統，其風量係由一台送風機以管路分送二倉，並經過穀倉筒內之穀物以進行乾燥。為簡化整個系統之分析，可以將其類比為一般之串並聯電路。整個系統因此可視為一個電阻分路，各風管對所送之風量Ｑ均有一定的阻力Ｒ，而風機所產生之壓力Ｐ則可類比為電壓。在實際的情況下，其間之關係並不盡然為線性，不過在低風量下，將其關係視為線性應不致產生太大的誤差，其結果應可接受。

分析：

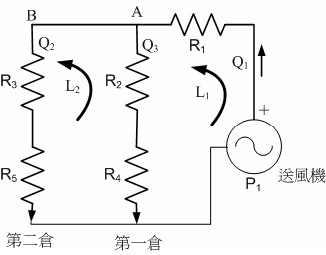
此種類比係簡化風壓、風量與風阻間之關係為線性，故可以利用電路進行類比模擬。在系統中，送風機係將大氣壓的空氣壓縮，提高其風壓。故若以大氣壓比擬為電路之接地時，高壓空氣經過風管、穀倉中之穀層，其後將再排放至大氣中，其最後風壓又恢復為大氣壓。因此，以電路模擬時，可改用下圖所示。其中R1為主管之風阻，R2與R3則為分岐管之風阻，然後通過穀層，其風阻較大，分別為R4與R5。

圖5.通風系統之電路模擬

在單位方面，風壓常以mm水柱高表示其範圍100mmH ₂O；風量以cmm表示。依風阻之定義，其關係式為P=QR，其單位應為mmH ₂O/cmm。實際上之風阻可參考穀物乾燥之相關書籍。其值域約為3,000-5,000mmH ₂O/cmm之間，榖物之風阻則此值之數十倍。故若以１風歐姆（ＷΩ）＝１mmH ₂O/cmm，則可使用ＫＷΩ為單位計算。利用兩迴圈及點Ａ之風流量建立聯立方程式之關係式，其相關程式演算如下：

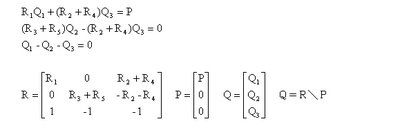
程式內容：


function Qflow=duct_flow(p,r)
% Prog using circuit to find airflows in a system.
% Inputs:
%   p: Prssure of fan. mmH2o
%   r: wind resistances  r=[r1 r2 r3 r4 r5], in KWohms.
% Outputs:
%   Qf: Airflow, in cmm [q1 q2 q3]
% Example: Qf=duct_flow(100,[1 2 2 10 10])
P=[p 0 0]';
R=[r(1) 0 r(2)+r(4);0 r(3)+r(5) -r(2)-r(4);1 -1 -1];
Q=R/P;Qflow=Q';

執行例：


>> Qf=duct_flow(100,[1 2 2 10 10])

Qf =       14.286       7.1429       7.1429

此處風量之單位為cmm。

10.2 範例四：穩態熱傳導的問題

穩態熱傳導的問題

熱傳導是溫差產生的熱能流動，其流動速率與材料之熱阻係數有關。其公式如下：


  q = Q/t 
    = k A (Th-Tc)/d 
    = ΔT/(d/kA) 
    = Δ/R

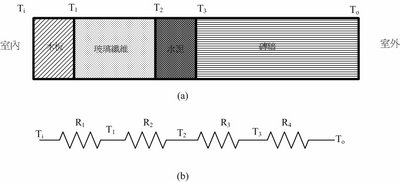
其中d為材料之厚度，Ａ為截面積，k為熱導係數，其單位為W/[mK]。R則為熱阻，等於d/kA。熱阻的觀念可以用來模擬電路，並進行解析。圖為一道牆由木板、玻璃纖維、水泥及磚牆等材料。這些材質之熱導係數可參閱此網站 http://hyperphysics.phy-astr.gsu.edu/hbase/thermo/heatcond.html#c1。其他相關值如下：

材質名稱	熱導係數W/[mK]
磚牆	0.6
木材	0.12-0.04
石膏	0.08
玻璃纖維	0.04
玻璃	0.8
水泥	0.8
鐵板	50.2
水	0.6

熱阻與電阻之類比關係

將各層產生之熱阻，以電路的方式進行串聯，即可形成類似網路，並計算各層之溫度。其各層間之關係式如下：

　　　　
以矩陣表示，即為[A][T]=[C]。其溫度T可解如後：


    [T]=[A]/[C]

程式說明

程式heat_wall.m可以執行上述之操作。輸入項包括內外溫度(ti,to)、各層熱導係數(k)、厚度(thick)及截面積(area)等。執行後即可得到溫度分佈及熱流(q)等。

程式內容


function [T,x,q]=heat_wall(ti,to,k,thick,area)
% Prog calculating heat transfer through a wall.
% Inputs:
%   ti,to: inside & outside temperature, C
%   k: thermoconductivities of each layer, W[m.C]
%   thick:thickness of each layer, mm
%   area:the crosssection area, m^2
% Outputs:
%   temp:[heatflow & temperatures at each layer, W/m^2,C
% Example:
%  [T,x,q]=heat_wall(20,-10,[0.08 0.04 0.12 0.6],...
%          [10 125 60 50])
% Designed by D.S. Fon. Date: Nov. 26, 2006
if nargin<5, area=1;end
R=thick./k/area/1000;
nn=length(thick);C=zeros(1,nn);
CC=-eye(nn)+[[zeros(nn-1,1) eye(nn-1)];C];
A=[R',CC(:,2:end)]
C=[ti C(2:end-1) -to]';
x=[0 cumsum(thick)];
TT=A/C;q=TT(1);T=[ti TT(2:end)' to];
line(x,T,'marker','s')
xlabel('distance,mm')
ylabel('Temperature,C')

執行例：

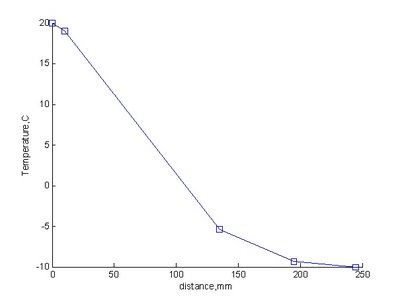
設室內溫度為攝氏25度，室外為-10度。牆壁由內而外為木板(50mm)、玻璃纖維(100mm)、水泥面(20mm)、磚牆(200mm)，其對應之熱導係數分別為[0.12 0.04 0.8 0.6]。以此代入heat_wall程式中執行，得其結果：


>> [T,x,q]=heat_wall(20,-10,[0.08 0.04 0.12 0.6], [10 125 60 50])

A =

 0.1250    1.0000         0         0
 3.1250   -1.0000    1.0000         0
 0.5000         0   -1.0000    1.0000
 0.0833         0         0   -1.0000

T =
20.0000   19.0217   -5.4348   -9.3478  -10.0000

x =
  0    10   135   195   245

q =
 7.8261

其溫度分佈則如下圖：

沿軸溫度分佈圖

若內外側均採用木板，但內側厚度為100mm，外側為60mm，則其溫度分佈及熱流量如下：


>> [T,x,q]=heat_wall(20,-10,[0.08 0.04 0.12 0.6 0.08], [100 125 60 50 60])

A =

 1.2500    1.0000         0         0         0
 3.1250   -1.0000    1.0000         0         0
 0.5000         0   -1.0000    1.0000         0
 0.0833         0         0   -1.0000    1.0000
 0.7500         0         0         0   -1.0000

T =

20.0000   13.4307   -2.9927   -5.6204   -6.0584  -10.0000

x =
  0   100   225   285   335   395

q =

 5.2555

其溫度變化雖不大，但熱流量則有顯著的減少。

10-2 範例五：簡易之熱流分析

範例五：熱流問題

熱流的問題有時是一個平面分佈的情形。以下圖為例，在一個侷限的空間中，設將其分為四等分，每等分之接觸面積均相同。進口處之溫度為Ｔi，出口溫度為To，其餘外圍部份均為絕熱狀態，熱流停止，故接觸之該面溫度不起變化。同樣，若將熱流比做電流，則可以形成類比電路如圖(b)，設其進出介面時之熱阻以Ｒ表示。由於材質假設相同，其截面積也相同，故每一介面之熱阻也應相同。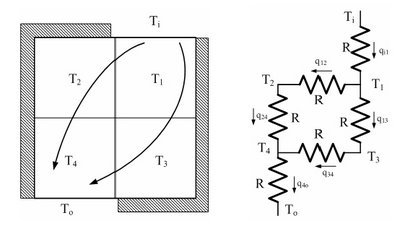

　　　　
由電路之網絡觀之，熱流由外界流入T1節點，再分兩路流入T2與T3兩節點，最後滙流至T4，由此流至外界To。注意T1不能直接流至T4，因為兩者之接觸面積為零。因此由電路網絡很容易解出此並聯電路之解。由於熱阻均相同，在公式中可以不考慮。其熱流之平衡式可表列如下：

　　
根據熱流之關係，可以改變為：

　　　
由上式得到的結論是任何一點之溫度應為其相連週圍之溫度點之平均值。其聯立方程式最後為下列型式：

程式內容


function [T]=heat_plate(ti,to)
% Prog calculating heat transfer through a plate.
% Inputs:
%   ti,to: input & output temperature, C
% Outputs:
%   temp:temperatures at each layer,C
% Example:
%  T=heat_plate(20,-10)
C=[ti 0 0 to]';
A=[3 -1 -1 0;-1 2 0 -1;-1 0 2 -1;-1 -1 0 3];
TT=A/C;T=[ti TT' to];

執行範例


>> T=heat_plate(100,-10)
T =  100.0000   68.5714   52.8571   52.8571   37.1429  -10.0000

深入分析

如果要更確的數據，則可以增加方格，但其運算方程式之數目亦將增加。例如增加為3X3方格，則總格數為九格，必須要有九條方程式才能處理。根據前面所述之原理，某格之溫度等於其鄰近方格溫度之平均值。因此T5之溫度應為T2、T4、T6、T8等四溫度之平均值；而T3與T7則僅為鄰近兩項值之平均，其餘均為三個鄰近值之平均。

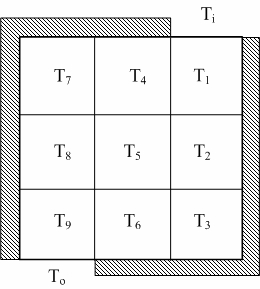
若將其改為矩陣AT=C之型式，則各矩陣之內容變為：

程式內容

　 　　
function [T]=heat_plate3(ti,to)
% Prog calculating heat transfer through a plate by 3x3.
% Inputs:
%   ti,to: input & output temperature, C
% Outputs:
%   temp:temperatures at each layer,C
% Example:
%  T=heat_plate3(20,-10)
C=[ti 0  0  0  0  0  0  0 to]';
A=[3 -1  0 -1  0  0  0  0  0;
　-1  3  0 -1 -1  0  0  0  0;
   0 -1  2  0  0 -1  0  0  0;
  -1  0  0  3 -1  0 -1  0  0;
   0 -1  0 -1  4 -1  0 -1  0;
   0  0 -1  0 -1  3  0  0 -1;
   0  0  0 -1  0  0  2 -1  0;
   0  0  0  0 -1  0 -1  3 -1;
   0  0  0  0  0  -1 0 -1  3];
TT=A/C;T=reshape(TT,3,3);

執行例：


>> T=heat_plate3(20,-10)
T =
12.4272    8.2767    6.0922
 9.0049    6.3107    3.9078
 6.5291    4.0534   -0.6796

10.3 範例六、det & rank 指令之應用

det & rank 指令

利用左除法的求解過程甚為簡單，但有時並不一定有解，有時也可能有多組解。聯立方程式中，型式上其變數與方程式之數目相同，應可以得解。但有些方程式是相依的，或者其中方程可能由其他兩式相互加減而得的結果，此時即無法無法獲得唯一解，因此過程上仍需先行檢驗。行列式值與聯立方程式求解有密切的關係。其值若為零，所得之解可能為非唯一組解；若不為零，則可能得到一組解。在MATLAB中，可以使用位階指令rank檢驗。

舉例：

一魔術函數造成之矩陣Ａ，其行列值及位階分別由det & rank 指令進行檢驗：


　　A=magic(4);
　　det(A)
　　rank(A)

ans =     0
ans =     3

矩陣Ａ雖為4x4，利用行列值檢視，其值為det(A)=0，表示無法獲得單一解。同樣利用rank位階指令檢查，其結果為3階，兩者均顯示與矩陣Ａ相關之聯立方程式可能為多組解。

要檢測一組聯立方程式是否有解，使用上述rank的指令功能可以研判。例如檢測AX=C這一組聯聯立方程式，先求rank(A)與 rand([A C])之階值，後者[A C]稱為增廣矩陣(Augrmented matrix)。若所得兩個階值相同，且其階值等於變數個數時，應為有解且其解屬唯一。若階值小於變數個數時，其解應為多數解，其變數可用兩者之差數之線性組合表示。

範例：


　A=[6 -3 5;10 4 -8;-6 2 3];C=[12 -20 15]';
　R1=rank(A)
　R2=rank([A C])

　R1 =     3
　R2 =     3

由於兩者之階值相同，表示其解存在且為唯一。下面就一個多數解的例子進一步說明：


　A=[3 2 1; 10 -25 5];C=[5000 2000]';
　R1=rank(A),R2=rank([A C])
　R1 =     2
　R2 =     2

顯然這組方程式應有解，但由於階數2小於變數個數3，故其解為多數解。利用左除法亦可得到其中一解，即令T3等於零時，所得之答案。其過程如下：

範例六：

有一電路如圖，接於一電源Ｖ上。試求通過各電阻器上之電流。

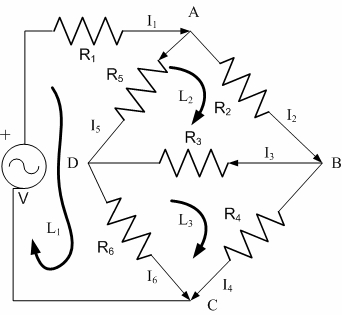
根據克希荷夫Kirchhoff定律，可以選定三個迴圈建立屬於電壓降之三項聯立方程式，及電流經由Ａ、Ｂ、Ｃ三點產生分流時所能建立之四個關係方程式得之：

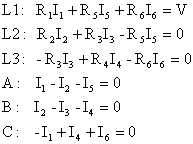
整理此組聯立方程式，其電流變數Ｉ有五項，其方程式有五組，故應可得解。茲以矩陣[R][I]=[V]表示，利用左除法即為[I]=[R]/[V]。其各變數矩陣分別為：

程式內容


function Curr=ele_amp(v,r)
% Prog using Kirchihoff's law to find the currents in a circuit.
% Inputs:
%   v: Voltage of generators. volts
%   r: the resistances  r=[r1 r2 r3 r4 r5 r6], in Kohms.
% Outputs:
%   Curr: currents through resistors [c1 c2 c3 c4 c5 c6], in mA
% Example: current=ele_amp(100,[1 1 2 5 5 10])
V=[v 0 0 0 0 0]';
R=[r(1)   0     0    0  r(5)  r(6);
    0  r(2)  r(3)    0 -r(5)     0;
    0     0 -r(3) r(4)     0 -r(6);
    1     0    -1    0    -1     0;
    0     1    -1   -1     0     0;
   -1     0     0    1     0    -1];
Current=R/V;Curr=Current';

執行結果：


>> current=ele_amp(100,[1 1 2 5 5 10])
current =       8.0338        17.97       3.1712       14.799       4.8626       6.7653
>> current=ele_amp(100,[0 1 2 5 5 10])
current =
     8.7356        19.54       3.4483       16.092       5.2874       7.3563

10.3 虛反矩陣指令pinv之應用

pinv指令

在多數解的例子中，有時並不是僅要將其中一變數設定為零之解。為使整個系統得到最佳化，亦可利用pinv指令求得最小模組之合理解。pinv(A)又稱為虛反矩陣(pseudoinverse)，其功能與反矩陣之計算相同，但它會基於svd(A)函數(或稱奇異值分解函數)之計算方式，求得一個不是屬於全階之矩陣A之反矩陣。這是長方形矩陣求解時，在多重解中求其反矩陣之折衷方式。故若矩陣A為方矩陣或非零矩陣，則其結果應與inv(A)相同。只是在這樣的狀況，寧可使用inv(A)較為省事。處理這些長方矩陣或特異矩陣時，使用pinv(A)會有意想不到的效果。其解法是根據反矩陣法：


A=[3 2 1; 10 -25 5];C=[5000 2000]';
>> T=inv(A)*C
??? Error using ==> inv
Matrix must be square.

T=pinv(A)*C 

T =
      1203.9
      485.16
         418

上面之例因為Ａ不是方形矩陣，故求其反矩陣時會有錯誤的信息，但若用虛反矩陣指令pinv，反而相安無事，這是將T1、T2以其餘一變數T3表示之情況下，求得其最小平方之組合。其結果是否合用則端視問題之限制與應用而定。 PINV(A,TOL) 之指令後面另有參數TOL，可以輸入容許值。其預設值為MAX(SIZE(A)) * NORM(A) * EPS(class(A))，讀者可參考手冊之說明，以瞭解其使用方法。

rref指令

在處理聯立方程式時，若直接有解，應可利用左除法得到其答案。若為多數解，則需要將其重組並簡化至梯形的表列方式，將某些變數設定為自變數，並將其餘因變數之係數均轉換為1。此時可以利用rref([A C])這個指令達到目的。這個指令執行結果，會產生一個增廣矩陣，其內容為[A C]。以前述之T組變數為例：


　M=rref([A C]) 

　M =
           1            0      0.36842       1357.9
           0            1    -0.052632       463.16

最後簡化之梯形聯立方程式為：


　T₁+0.3684T₃=1357.9
　T₂-0.0526325T₃=463.16

此時之聯立方程式經過rref這個指令會將結果簡化。

例題：

下面為一農場作業之資料，比較重要的作業可以分為整地、噴藥及收割等三項。下表為甲乙兩工人對個別作業每公頃所需之作業時數。設若此兩工人今年總工作時數分別為100及150小時，試求其今年各人總作業面積為多少。


小時／公頃 整地作業 噴藥作業 收割作業
========== ======== ======== ========
甲工人       3          5       8
乙工人       2          4       3

設x, y ,z分別為整地、噴藥及收割作業之作業面積數，則甲工人一年之工作情形可以下列方程式表示：


甲工人：3x + 5y + 8z=100
乙工人：2x + 4y + 3z =150

顯然這是一個多數解的系統。設


>> A=[3 5 8;2 4 3]
A =
     3     5     8
     2     4     3
>> b=[100 150]'
b =
   100
   150

利用增廣矩陣可以縮減成簡易之x y z系統：


>> rref([A b])
ans =
    1.0000         0    8.5000 -175.0000
         0    1.0000   -3.5000  125.0000

解之，


　x + 8.5z=-175
    y-3.5z =125

或　x = 8.5z-175, y=125 +3.5z
在這種情況下，由於變數在均為正值之限制之下，故應可以得到一個範圍解。

10.4 最小平方解法

當一個系統之聯立方程式個數大於未知數之數目時，會形成過度確定性系統(overdetermined system)。此時，反矩陣法已無法應用，只能用左除法求解。但這種解如同多數解的過程一樣，必須尋最小平方的技巧,使解能夠以最接近所有點為準，成為一般所謂之回歸公式。茲以下面例子做介紹：

設有一方程式的關係式為y= a x₁+b x₂+c x₃想適配下列資料：


y x₁ x₂ x₃
 3  2  3  1
 6  3 -2  4
-5 -5  3  6
 4  2  7  3
 2  4  8 -7

依問題之需要，可利用rank指令執行如下：


A=[2 3 1; 3 -2 4; -5 3 6; 2 7 3; 4 8 -7];
C=[3;6;-5;4;2];
R1=rank(A), R2=rank([A C])

由階數R1及R2觀之，兩者不相同，故無法以正常方式得解。然而利用左除法B=A/C仍可以得到相關係數，因此得到此函數為：


B=A/C
R1 =     3
R2 =     4
B =
    1.442
   -0.067601
    0.4352

y= 1.442 x₁ -0.067601x₂+0.4352 x₃

然而，此結果並非其真實解，而是利用最小平方法求得。若以此解作驗證，即y=A*B，其結果為：


A*B
ans =
   3.1163
   6.2018
  -4.8014
   3.7163
   2.1806

顯然與原值[ 3 6 -5 4 2]仍有誤差。只是因採用最小平方的關係，可以求得最接近之數。最小平方的取法是將各數項之平方值之和以fmins求得最小值。即：


J=Σ_i=1⁵[ax_1i+bx_2i+cx_3i-y]²

最小平方之應用將在第十一章統計與迴歸部份進一步說明。

10.5 網絡分析之應用

梯形數值分析法(Trapezoidal Numerical Integration)

數值分析法常用以解積分的問題，積分之解法依問題的性質有不同的方式。比較簡單的方式是將其分成細段，然後細段之微小面積，加總後成為最後的結果。此種積分稱為梯形法。

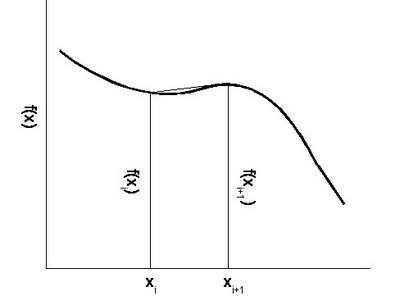
利用梯形法可以解決複雜函數之積分問題。在MATLAB之中，也有相同的指令，TRAPZ，其語法如下：


  Z = trapz(Y)
  Z = trapz(X,Y)
  Z = trapz(...,dim)

若參數中僅有Ｙ項，則其分段值設為1；若區段不為１，則可就其結果乘以需要之區段值。Ｙ值可為複數，可以針對實數及虛數部份分開積分。若有對應之X值，則X與Y應為成對的向量，此時區間可不必均等值。若為長方形矩陣，則可利用第三個參數dim決定是進行行向(=1)或列向(=2)積分。

下面的程式則是就f(x)=1/x函數，在區間A=1與B=2之間作積分，設此區間分成N=10段，進行比較直接運算與使用trapz指令所得的結果：


% trapezoid.m
% Find the area under a curve.
%
f=@(x) 1./x;
A=1;B=2;N=10;
x=linspace(A,B,N);
y=f(x);
Ts=0;
for i=1:N-1,
   DX=x(i+1)-x(i);
   Ts=Ts+DX*(y(i+1)+y(i))/2;
end
Area=trapz(x,f(x));
disp(['¨Using trapezodal law:',num2str(Ts)]);
disp(['¨Using Matlab trapez command:',num2str(Area)]);

執行trapezoid.m程式後，結果如下：


>> trapezoid
¨Using trapezodal law:0.69392
¨Using Matlab trapez command:0.69392

兩者之結果完全吻合。讀者可使用不同之函數及區間，作不同的演算，並相印證。

三角形面積

前面已經討論過如何應用程式指令計算由三個節點構成的三角形面積。但在有限元素法的作業上，通常均採用直接與座標點具有關連的結果，即：

這是一個行列式值，也可以看成矩陣。

其對應的三角形面積Ｓ＝det(A)/2。此時(x1, y1)、(x2, y2)、(x3, y3)分別代表三角形的三個頂點。例如：某三角形之三個頂點分別為(5, 4)、 (6, 1)、(10, 5)，則其Ａ及面積Ｓ分別為：


>> A=[1 5 4;1 6 1;1 10 5]

A =

     1     5     4
     1     6     1
     1    10     5

>> S=det(A)/2

S =

     8

其面積為8個單位。

任意形狀之面積

求一個任意三角形之面積並不稀奇，問題是若要求任意形狀之面積時，其實可以將其分割為成許多大小不同的三角形，用程式計算後，再予以加總。因而再複雜的形狀，也可以因而得解。這就是網絡分析的重點。以下圖為例，這個多邊形由六點組成，若區分為三角形則可改由四個三角形組合而成。設其各點之對應座標及各三角形點之組合如下表：


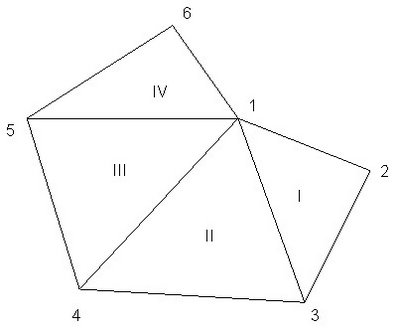
表一、多邊形各點對應值
點號       X       Y    Z(高度)
=====    ====    ====   ======
 1         1       6      3
 2         3       5      5
 3         2       2      6
 4        -2       3      8
 5        -4       6      5
 6         0       8      4

表二、三角形編號對照表


三角形編號      對應點
==========  =i=   =j=   =k=
    1        1     2     3
    2        1     3     4
    3        1     4     5
    4        1     5     6

表一中另列有Z值，此值為對應該平面點之高度或某一特定函數。因此，除計算ＸＹ面之多邊形面積之外，若為三度空間之座標，實際上亦可計算其體積、上層之表面積等。

計算體積時，可以就每一個三角形底面積乘以對應之高（即為Ｚ），為獲得平滑資料，可以取其三頂點對應之高度作平均，亦即每一個三角形對應之體積應為：


Ｖ＝[det(A)/2] (Zi+Zj+Zk)/3

其中之i、j、k分別為每個三角形之對應頂點（即表二之值）。

表面積之求法較為複雜。基本上曲面之表面必須利用積分的形式，分成三角形之網絡亦可求得，此時必須針對三角形之頂部表面考慮，然後進行累加。亦即，設z=u(x,y)為座標點(x,y)之函數，則

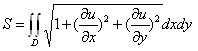
此式中，U為x,y之函數，亦可視為第三座標z值。在三角形之最小單位中，可以利用其三個頂點i, j, k求得其關係式，可聯立如下：


  Ui=u(xi,yi)
  Uj=u(xj,yj)
  Uk=u(xk,yk)

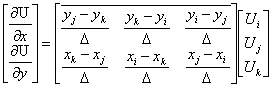
程式內容


% trivolume.m
% Using trianglular method finding irregular areas
x=[1 3 2 -2 -4 0];%nod point
y=[6 5 2 3 6 8];
z=[3 5 6 8 5 4];
elements=[1 2 3;1 3 4;1 4 5;1 5 6];%trangle code
TA=0;TV=0;TS=0;
for i=1:length(elements(:,1)),
   p1=elements(i,1);p2=elements(i,2);p3=elements(i,3);
   A=[1 x(p1) y(p1);1 x(p2) y(p2);1 x(p3) y(p3)];
   delta=abs(det(A))/2;
   TA=TA+delta;%cumulative area
   TV=TV+delta*(z(p1)+z(p2)+z(p3))/3;%cum. volume
   B=[y(p2)-y(p3) y(p3)-y(p1) y(p1)-y(p2);
       x(p3)-x(p2) x(p1)-x(p3) x(p2)-x(p1)];
   ZZ=[z(p1) z(p2) z(p3)]';
   UU=B*ZZ/det(A);
   ES=delta*sqrt(1+UU(1)^2+UU(2)^2);
   TS=TS+ES;
end
disp(['The bottom area:',num2str(TA)]);
disp(['The total volume:',num2str(TV)]);
disp(['The total surface area:',num2str(TS)]);

執行範例：


>> trivolume
The bottom area::23.5
The total volume::118.8333
The total surface area::34.444

10.6 二個桶子間之水位問題

不同水位之兩個桶子,其下用管路相通。當其開關打開後，兩桶之水位隨時間而變化，水位高著向水位低者流動，其流動速率與兩桶水位差成正比。設每公分之水位差之流動量為Ｃ[cm³]，兩桶之斷面直徑分別為[D₁、D₂]cm，水位高度分別為[U₁、U_２]cm，則在管路之流動量Ｖ為：


  V=C*H*(U₁-U₂)
　U₁=U₁-V/A₁
  U₂=U₂+V/A₂

式中，H為每次計算時之時段，A ₁A ₂分別為水桶之斷面積，U ₁、U ₂則隨著時間而變化。

程式設計

下面之程式係以上式為計算基礎，其輸入分三種方式，即使用預設資料、使用參數輸入與逐項輸入之方式：

預設資料：pail2pail
使用參數輸入：pail2pail(U,D,C,Delt)
逐項輸入：pail2pail(1)

程式內容


function pail2pail(U,D,C,Delt)
% pail2pail.m
% program to calculate waterflows between two pails.
% U1,U2:water levels for each pails, cm
% D1,D2:diameters of both pails, cm
% T:time elapsed through the experiment.
% C:flow coefficent, in cm^3/cm of water level difference.
% designed by D.S. Fon, BIME, NTU. Date:Nov. 26,2006
if nargin==0,
U1=20;U2=10;D1=5;D2=5;C=1;delt=1;
elseif U==1,
U1=inopt1('A. Input water level in Pail No.1,cm',[50 0 500]);
U2=inopt1('B. Input water level in Pail No.2,cm',[0 0 500]);
D1=inopt1('C. Input diameter of pail 1,cm',[5 0 500]);
D2=inopt1('D. Input diameter of pail 2,cm',[5 0 500]);
C=inopt1('E. Input flow coefficient,cm^3/cm',[1 0 10]);
delt=inopt1('F. Input time interval,seconds',[1 0.1 10]);
else
U1=U(1);U2=U(2);D1=D(1);D2=D(2);
end
A1=pi*D1^2/4;A2=pi*D2^2/4;
T=0;i=0;
clf;
disp('  Time      Pail 1 Level  Pail 2 Level');
disp('========    ============  ============');
while abs(U2-U1)>delt,
fprintf(1,'%8.3f    %10.4f  %10.4f/n',T,U1,U2);
T=T+delt;i=i+1;
vel=C*delt*(U1-U2);
U1=U1-vel/A1;U2=U2+vel/A2;
f1(i)=U1;f2(i)=U2;Tx(i)=T;
line(Tx(i),f1(i),'Marker','o');
line(Tx(i),f2(i),'Marker','s');
end
j=fix(i/3);
line(Tx,f1,'color','red');
line(Tx,f2,'color','blue');
line([0 Tx(end)],[(f1(1)+f2(1))/2 (f1(1)+f2(1))/2]);
text(Tx(j),f1(j),'/leftarrow---U1');
text(Tx(j),f2(j),'/leftarrow---U2');
xlabel('Time, seconds');
ylabel('Water levels, U1 & U2');

function [kk]=inopt1(A,s)
while 1
      mtxt=['(',num2str(s(2)),'-',num2str(s(3)),')[',...
          num2str(s(1)),']=='];
      kk=input([A,mtxt]);
      if isempty(kk), kk=s(1);end
      if kk>=s(2)|kk<=s(3), return;end
      disp('*****Exceeding the limit, please reinput*****')
end

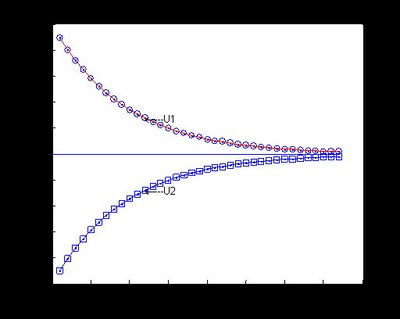
執行範例


>> pail2pail(1)
A. Input water level in Pail No.1,cm(0-500)[50]==>
B. Input water level in Pail No.2,cm(0-500)[0]==>
C. Input diameter of pail 1,cm(0-500)[5]==>
D. Input diameter of pail 2,cm(0-500)[5]==>
E. Input flow coefficient,cm^3/cm(0-10)[1]==>
F. Input time interval,seconds(0.1-10)[1]==>
Time      Pail 1 Level  Pail 2 Level
========    ============  ============
0.000       50.0000      0.0000
1.000       47.4535      2.5465
2.000       45.1664      4.8336
3.000       43.1123      6.8877
4.000       41.2674      8.7326
5.000       39.6104     10.3896
6.000       38.1222     11.8778
7.000       36.7856     13.2144
8.000       35.5851     14.4149
9.000       34.5069     15.4931
10.000       33.5386     16.4614
11.000       32.6688     17.3312
12.000       31.8877     18.1123
13.000       31.1861     18.8139
14.000       30.5560     19.4440
15.000       29.9901     20.0099
16.000       29.4818     20.5182
17.000       29.0253     20.9747
18.000       28.6153     21.3847
19.000       28.2470     21.7530
20.000       27.9163     22.0837
21.000       27.6192     22.3808
22.000       27.3524     22.6476
23.000       27.1128     22.8872
24.000       26.8976     23.1024
25.000       26.7043     23.2957
26.000       26.5307     23.4693
27.000       26.3748     23.6252
28.000       26.2348     23.7652
29.000       26.1090     23.8910
30.000       25.9960     24.0040
31.000       25.8946     24.1054
32.000       25.8035     24.1965
33.000       25.7216     24.2784
34.000       25.6481     24.3519
35.000       25.5821     24.4179
36.000       25.5228     24.4772

這是產生的兩桶之水位變化圖

10.7 多個桶子水位問題

多桶子並列成一排，底下以旁通管接通，若其中一個水桶之水位為Ui，則其與相鄰之水桶流水量Ｖ應為左右兩流量VL、VR之和，即：


　 VL(i)=[U(i-1)-U(i)]*C*DT
　 VR(i)=[U(i+1)-U(i)]*C*DT
    V(i)=VL(i)+VR(i)
        =[U(i-1)-2*U(i)+U(i+1)]*C*DT/A(i)

上述所討論為通式，但實際上前後兩側之水桶均僅有一個旁通管，故要特別處理，即：


     V(1)=[U(2)-U(1)]*C*DT/A(1)
   V(end)=[U(end-1)-U(end)]*C*DT/A(1)

經過DT的時間後，各桶內水位可依下式調整之：


   U(i)=U(i)+V(i)

程式結構

程式結構仍然與前述之二桶水位相同，只是現在Ｕ與Ｄ均改為向量，而且其大小應相同。本程式增加一個最終時間Ｔ，使程式超過此時間時可以停止運算。

同樣，此程式若無參數，則可使用預設資料，若打入pails(1)，則會逐項輸入，若直接餵入參數，則會依設定之參數執行，但需注意其大小應一致。

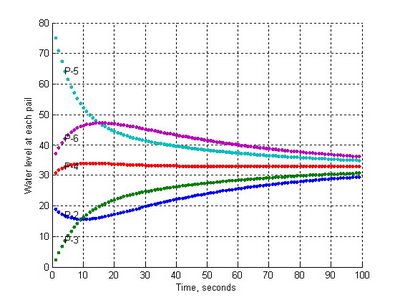
執行結果，各桶之水位會印出，而且會繪出各桶之水位變化圖。

程式內容


function [ff]=pails(U,D,C,delt,T)
% pails.m
% program to calculate waterflows between pails.
% U:water level of pails, cm
% D:diameter of pails, cm
% T:time elapsed through the experiment.
% C:flow coefficent, in cm^3/cm of water level difference.
% Designed by D.S. Fon, Bime, NTU, Date:Nov. 26,2006
while 1
if nargin==0,
   UU=[20 0 30 80 35];DD=[5 5 5 5 5];C=1;delt=1;T=100;
elseif U==1,
   UUx=[20 0 30 80 35];DDx=[5 5 5 5 5];Cx=1;deltx=1;Tx=100;
   disp('Enter following values in vector==> ')
   U1=input('Initial water level of pails,cm==> ','s');
   if isempty(U1), UU=UUx; else UU=str2num(U1);end
   D1=input('Diameter of pails,cm==> ','s');
   if isempty(D1), DD=DDx; else DD=str2num(D1);end
   T=input('Input the total elapsed time, seconds==> ');
   if isempty(T), T=Tx;end
   delt=input('Input a time interval, seconds==> ');
   if isempty(delt), delt=deltx;end
   C=input('Input flow coefficient, cm^3/cm ==>');
   if isempty(C), C=Cx;end
else
       UU=U;DD=D;
end
AA=pi*DD.^2/4;
npail=length(UU);
tt(1)=0;i=0;nn=ceil(T/delt);ff=zeros(nn,npail+1);
clf;
ff(1,:)=[0, UU];
for i=2:nn;
   tt(i)=delt*(i-1);
   for j=2:npail-1
       dU(j)=(UU(j-1)-2*UU(j)+UU(j+1))*C*delt/AA(j);
   end
   dU(1)=(UU(2)-UU(1))*C*delt/AA(1);
   dU(npail)=(UU(npail-1)-UU(npail))*C*delt/AA(npail);
   UU=UU+dU;
   ff(i,:)=[tt(i) UU];
   line(tt(i),UU,'Marker','.');
end
m=5;if m>npail, m=1;end
for i=2:npail+1
   text(tt(m),ff(m,i),['P-',num2str(i)]);
end
xlabel('Time, seconds');
ylabel('Water level at each pail');
grid on;figure(gcf);
yn=input('Continue?(Y/N)[Y]==> ','s');
if ~isempty(yn) & upper(yn)~='Y', break; end
end

執行結果：


>> pails

ans =

     0   20.0000         0   30.0000   80.0000   35.0000
1.0000   18.9814    2.5465   31.0186   75.1617   37.2918
2.0000   18.1444    4.8336   31.8167   70.9848   39.2205
3.0000   17.4665    6.8857   32.4373   67.3722   40.8383
4.0000   16.9276    8.7259   32.9152   64.2417   42.1896
5.0000   16.5099   10.3756   33.2787   61.5231   43.3127
6.0000   16.1975   11.8544   33.5507   59.1572   44.2402
7.0000   15.9763   13.1806   33.7499   57.0933   44.9999
8.0000   15.8339   14.3706   33.8911   55.2886   45.6158
----------------------------------------------------------
95.0000   29.3899   30.7720   33.0040   35.2304   36.6036
96.0000   29.4603   30.8153   33.0037   35.1870   36.5337
97.0000   29.5293   30.8578   33.0034   35.1444   36.4651
98.0000   29.5970   30.8994   33.0032   35.1026   36.3978
99.0000   29.6633   30.9402   33.0030   35.0616   36.3319

執行後之水位變化圖

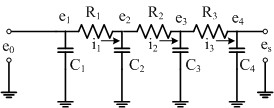
10.7 電路中CR過濾器之計算

一組RC電路之組成亦可類比於並列之水桶中之水流。其電路圖如下：

R-C電路圖

依據歐姆定律及電荷守衡法則，電流與電壓間之關係為：


i1=(e1-e2)/R1
i2=(e2-e3)/R2
---
d(e2)/dt=(i1-i2)/C2
d(e3)/dt=(i2-i3)/C3
---

將前半部電流之公式代入後半部電壓梯度之公式，其結果將與並列水桶類似，即：


dE(i)=(E(i-1)-2*E(i)+E(i+1))*A*delT/C(i)

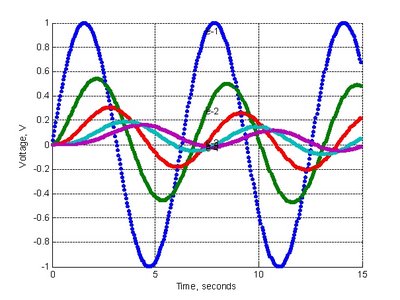
開始時電壓設為正弦曲線，即e1=sin(t)，然後依時序之演進計算其他點之對應值。下面程式是根據此項法則進行演算。此程式中電容數比電阻數多一，但也可以向量的形式輸入。程式之執行與前述10.6節相同。執行完畢時，會有其電壓變化比較圖。

程式內容


function [ff]=crfilter(RR,CC,N,T,E)
% crfilter.m
% program to calculate a multiple R-C circuit.
%     o----o----R---o--R---o--R---o-----o
%          |    |   |      |      |   
%          C    C   C      C      C   
%          |    |   |      |      |   
%     o----o----o---o------o------o-----o
%
% E:Voltage, V
% RR:resistors, ohms
% CC:Capacitance, microfaras.
% T:time elapsed through the experiment.
% Designed by D.S. Fon, Bime, NTU, Date:Nov. 26,2006
while 1
if nargin==0,
RR=[1 1 1 1 1];CC=[1 1 1 1 1];N=400;T=[0 15];
elseif RR==1,
RRx=[1 1 1 1 1];CCx=[1 1 1 1 1];Nx=400;Tx=[0 15];
disp('Enter following values in vector==> ')
r1=input('Resistors,ohms==','s');
if isempty(r1), RR=RRx; else RR=str2num(r1);end
c1=input('Capacitance,fara== ','s');
if isempty(c1), CC=CCx; else CC=str2num(c1);end
T1=input('Input starting & ending time, seconds== ','s');
if isempty(T1), T=Tx; else T=str2num(T1);end
n1=input('Input number of time interval== ');
if isempty(n1), N=Nx;end
end
AA=1./RR;Ts=T(1);Te=T(2);
delT=(Te-Ts)/N;
nn=length(CC);
ff=zeros(N,nn+1);EE=ones(1,nn)*sin(Ts);
clf;
ff(1,:)=[0, EE];
tt(1)=0;i=0;
for i=2:N;
tt(i)=Ts+delT*(i-1);EE(1)=sin(tt(i));
for j=2:nn-1
    dE(j)=(EE(j-1)-2*EE(j)+EE(j+1))*AA(j)*delT/CC(j);
end
dE(nn)=(EE(nn-1)-EE(nn))*AA(nn)*delT/CC(nn);
EE=EE+dE;
ff(i,:)=[tt(i) EE];
line(tt(i),EE,'Marker','.');
end
m=fix(N/2);
for i=2:nn+1
text(tt(m),ff(m,i),['e-',num2str(i-1)]);
end
xlabel('Time, seconds');
ylabel('Voltage, V');
grid on;figure(gcf);
yn=input('Continue?(Y/N)[Y]==> ','s');
if ~isempty(yn) & upper(yn)~='Y', break; end
end

執行結果：


>> crfilter

ans =

      0         0         0         0         0         0
 0.0375    0.0375    0.0014         0         0         0
 0.0750    0.0749    0.0041    0.0001         0         0
 0.1125    0.1123    0.0080    0.0002    0.0000         0
 0.1500    0.1494    0.0130    0.0005    0.0000    0.0000
 0.1875    0.1864    0.0191    0.0009    0.0000    0.0000
 0.2250    0.2231    0.0260    0.0016    0.0001    0.0000
 0.2625    0.2595    0.0339    0.0024    0.0001    0.0000
 0.3000    0.2955    0.0425    0.0035    0.0002    0.0000
 0.3375    0.3311    0.0519    0.0049    0.0003    0.0000
 0.3750    0.3663    0.0619    0.0065    0.0005    0.0000
 0.4125    0.4009    0.0725    0.0083    0.0007    0.0000
 0.4500    0.4350    0.0837    0.0104    0.0009    0.0001
 0.4875    0.4684    0.0954    0.0128    0.0013    0.0001
 0.5250    0.5012    0.1075    0.0155    0.0017    0.0001
 0.5625    0.5333    0.1200    0.0184    0.0021    0.0002
 0.6000    0.5646    0.1329    0.0216    0.0027    0.0003
 0.6375    0.5952    0.1461    0.0251    0.0033    0.0004
 0.6750    0.6249    0.1595    0.0288    0.0040    0.0005
 0.7125    0.6537    0.1731    0.0328    0.0048    0.0006
 0.7500    0.6816    0.1869    0.0370    0.0057    0.0008

------------------------------------------
14.8875    0.7315    0.4883    0.2074    0.0435   -0.0182
14.9250    0.7054    0.4859    0.2118    0.0473   -0.0159
14.9625    0.6783    0.4828    0.2159    0.0511   -0.0135

各節點之電壓變化

10.8 斜角指令之應用

diag對角指令

在前面討論到解一些聯立方程式時，主矩陣之安排及其內容是重要的項目。一般小程式中，其處理之矩陣不大，故應用時不會有什麼問題。以熱流之計算為例，依數值分析法題意中所分之元素A然很大，故其聯立之方程式仍然甚少。解題過程中不會發生容量與計算時間之問題。但在實際的數值分析題目中，其所分的節點很多(如一、二千點)，則所需處理的方程式增多，矩陣因而變大。不但佔去大部份之記憶體，而且浪費許多電腦計算的時間。而且在這些代表的矩陣中，大部份之項目均為零，不但沒效率，而且輸入均是困擾。為此，matlab有幾個特別處理對角項輸出入之指令，如：


A = eye(5)
A = diag(X)
A = diag(X,k)
Out=blkdiag(a,b,c)

指令eye主要在造出一個對角項為1之方形矩陣，前面也有許多實例之應用，如：


A=eye(5)
A =

  1     0     0     0     0
  0     1     0     0     0
  0     0     1     0     0
  0     0     0     1     0
  0     0     0     0     1

故若欲得到對角線上之相同元素項，可以直接用eye()乘以某一常數項即可。然而有些矩陣並不是方形，而且其所需填入之值也並不一定在對角線，此時若一一輸入又不勝其煩。此時必須借助diag這個指令。在使用這個指令之前，對於對角線方向之元素，必須有統一的說法，其指令才能得心應手。首先，可參考下圖方型矩陣的元素相關位置：

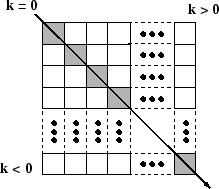
在矩陣中，凡是成45度角之元素均可稱為對角元素。為標明不同之位置，可以用一索引 k 表示。即在對角線正中間者可以設 k=0，在平行而且在此對角線之右上者，則依序以k=1, 2, 3,...表示，以下（左下角）者以k=-1, -2, -3,...表示。所以右上方k值為正；左下方k值為負。利用diag指令，Ｘ參數為一向量，即為欲填入對角線之值，可為行向或列向。k值之預設值為零，故不設定k值表示為對角線上之項目。例如：


>> A=diag([1 2 3 4])

A =

  1     0     0     0
  0     2     0     0
  0     0     3     0
  0     0     0     4

>> A1=diag([1 2 3 4],1)

A1 =

  0     1     0     0     0
  0     0     2     0     0
  0     0     0     3     0
  0     0     0     0     4
  0     0     0     0     0
>> A2=diag([1 2 3 4],-3)

A2 =

  0     0     0     0     0     0     0
  0     0     0     0     0     0     0
  0     0     0     0     0     0     0
  1     0     0     0     0     0     0
  0     2     0     0     0     0     0
  0     0     3     0     0     0     0
  0     0     0     4     0     0     0

上式，對角線元素之鉗入位置可見是依 k 值而定。不過有一點必須注意的是：一旦 k 的絕對值不同於零，所形成之方矩陣會變大，其大小正好比原來Ｘ項之長度加上k值之絕對值。所以對角線元素之位置愈偏離，其所得之矩陣會愈變大。故若要維持原來的大小(4 X 4)，則必須稍作改變，例如，A2可以調整如下：


>> A3=A2(3:end,1:end-2)

A3=

  0     0     0     0     0
  1     0     0     0     0
  0     2     0     0     0
  0     0     3     0     0
  0     0     0     4     0

若欲產生綜合兩對角之項目則可執行指令如下：


>> eye(5)+A3

ans =

  1     0     0     0     0
  1     1     0     0     0
  0     2     1     0     0
  0     0     3     1     0
  0     0     0     4     1

除此diag指令之外，MATLAB又有一個組合指令blkdiag，可以將任何大小之矩陣依矩陣之對角方向集合成一個大矩陣，例如：


>> C=[1 2 3;4 5 6]

C =

  1     2     3
  4     5     6

>> M=eye(3)

M =

  1     0     0
  0     1     0
  0     0     1

>> out=blkdiag(C,M,C)

out =

1     2     3     0     0     0     0     0     0
4     5     6     0     0     0     0     0     0
  0     0     0     1     0     0     0     0     0
  0     0     0     0     1     0     0     0     0
  0     0     0     0     0     1     0     0     0
  0     0     0     0     0     0     1     2     3
  0     0     0     0     0     0     4     5     6

10.8.2 稀疏矩陣之應用

稀疏矩陣是精簡一般含有零元素甚多的矩陣，僅就非零元素之位置加以陳述。此項作業可用sparse指令達成。其語法及相關指令如下：


 S = sparse(A)
 S = sparse(i,j,s,m,n,nzmax)
 S = sparse(i,j,s,m,n)
 S = sparse(i,j,s)
 S = sparse(m,n)
 TF = issparse(S)
 R = spones(S)

sparse 指令很簡單，它可以將一個含有許多零的元素矩陣改寫為位址表示，但其實質仍如原來之矩陣，功能相同，例如：


>> M=eye(5)

M =

    1     0     0     0     0
    0     1     0     0     0
    0     0     1     0     0
    0     0     0     1     0
    0     0     0     0     1

>> B=sparse(M)

B =

  (1,1)        1
  (2,2)        1
  (3,3)        1
  (4,4)        1
  (5,5)        1

產生之新矩陣Ｂ內僅記載具有非零元素之位置及數值。雖然Ｂ具上述型式，但其大小仍然與原來之Ｍ矩陣相同，而且可以直接與其他矩陣相互運算，有如與Ｍ矩陣運算一般。例如上述之稀疏矩陣B，其大小仍然與原先的一樣：


>> size(B)

ans =

    5     5

>> B*magic(5)

ans =

   17    24     1     8    15
   23     5     7    14    16
    4     6    13    20    22
   10    12    19    21     3
   11    18    25     2     9

若要恢後原來的型式，則可使用full指令復原，如：


>> full(B)

ans =

    1     0     0     0     0
    0     1     0     0     0
    0     0     1     0     0
    0     0     0     1     0
    0     0     0     0     1

除由原有之矩陣轉換外，sparse亦可由參數直接產生，其參數包括：


　　Ｌ = sparse(i,j,s,m,n,nzmax)

其中，i,j為非零元素之方位向量，而s為其對應之值向量，最終可以產生一個m x n大小之稀疏矩陣，亦即：


　 Ｌ(i(k),j(k)) = s(k)

這個指令主要用於某些相當大的矩陣，若全部依照傳統規矩輸入可能會使電腦炸掉！但利用這種方式直接轉為稀疏矩陣，則即使在小電腦中也可以從容執行。其中，nzmax為非零元素所能處理之最大數，不特別指定時，其值為length(s);而 i, j與 s之向量長度必須相同，s中若有零值項時會被忽略，連帶對應之i與j也被刪除。若i,j指向重複位置時，相同之值將被相加。

由於這個指令之輸入參數很多，實際上可以配find這個指令，找出某參數之非零元素，因為其輸入之三個參數正好為sparse之前三項輸入，例如：


M =

    2     0     9
    1     0     0
    0     4     0

>> [i,j,s]=find(M);
>> S=sparse(i,j,s,max(i),max(j))

S =

  (1,1)        2
  (2,1)        1
  (3,2)        4
  (1,3)        9

>> MM=full(S)

MM =

    2     0     9
    1     0     0
    0     4     0

採用稀疏矩陣主要目的在避免在運算過程中，使用超大矩陣以致記憶體空間不足，例如：
M = sparse(1:10,1:10,1) 產生一個對角元素為1之稀疏矩陣，其結果與M=sparse(eye(10))是相同的，問題是後者一定要透過實際的矩陣，已失去稀疏矩陣的原意。只是執行時，電腦將耗去較多時間，只是以時間換空間，應用上也是一個較好的選擇。

稀疏函數spfun

對於稀疏矩陣之非零元素與函數關係之處理，則可使用spfun，其語法如下：


f = spfun(@fun,S)

例如，設Ｓ為前述例中之稀疏矩陣，求其對Ｓ之非零元素作正弦函數：


>> f=spfun(@sin,S)

f =

  (1,1)       0.9093
  (2,1)       0.8415
  (3,2)      -0.7568
  (1,3)       0.4121

此處之fun可用函數之握把，其運算僅針對非零元素，時間上也可因而縮短。至於如何辨別Ｓ是否為稀疏矩陣，可以使用issparse(S)進行測試。此外另一個函數 spones(S)則可產生一結構與Ｓ相同之矩陣，但Ｓ中之非零元素部份均取代為1。例如：


>> spones(S)

ans =

  (1,1)        1
  (2,1)        1
  (3,2)        1
  (1,3)        1

矩陣之相關邏輯運算亦可在稀疏矩陣中應用。

處理稀疏矩陣之亂數指令sprandn/sprand

稀疏矩陣之均勻分佈及常態分佈可用sprand及sprandn指令。其語法如下：


 R = sprandn(S)｜sprand(S)
 R = sprandn(m,n,density)/sprand(m,n,density)
 R = sprandn(m,n,density,rc)｜sprand(m,n,density,rc)

亂數指令 sprandn(S)是產生與S結構相同的亂數，其值在０至１之間。sprandn(m,n,density) 則是產生m-x-n個稀疏矩陣之亂數，其分佈以density*m*n 為基準，其值域為0 <= density <= 1)。其中，rc為反覆條件(reciprocal condition)。rc可為以 lr <= min(m,n)之向量。亂數若以對角線作成對稱的分佈，則可使用sprandsym相關指令為之，其格式如下：


R = sprandsym(S)
R = sprandsym(n,density)
R = sprandsym(n,density,rc)
R = sprandsym(n,density,rc,kind)

轉換用指令spconvert

由於稀疏矩陣之格式與實際存檔資料之格式不同，故自檔案中讀入之資料必須經過spconvert指令處理：


S = spconvert(D)

上述過程中，可先在ASCII資料檔中編輯對應之[i,j,v] 或 [i,j,re,im] 欄位，然後轉為稀疏矩陣。資料需為每列三欄，若為四欄則可產生複數之矩陣。例如下面為 ASCII檔案，其名稱為 uphill.dat，內容為：


1    1    1.000000000000000
1    2    0.500000000000000
2    2    0.333333333333333
1    3    0.333333333333333
2    3    0.250000000000000
3    3    0.200000000000000
1    4    0.250000000000000
2    4    0.200000000000000
3    4    0.166666666666667
4    4    0.142857142857143
4    4    0.000000000000000

執行下列指令後，即可產生Ｈ之稀疏矩陣：


load uphill.dat
H = spconvert(uphill)

H =
  (1,1)       1.0000
  (1,2)       0.5000
  (2,2)       0.3333
  (1,3)       0.3333
  (2,3)       0.2500
  (3,3)       0.2000
  (1,4)       0.2500
  (2,4)       0.2000
  (3,4)       0.1667
  (4,4)       0.1429

10.8.3 spdiags稀疏對角指令

前文討論的對角元素處理指令已可隨意就斜角方向置入任意元素。實際上在解題時，尤其進行數值分析過程中，所形成之矩陣雖然很大，但百分之八、九十的空間大部份都是為零。對於資料處理方面是一種相當大的資源浪費。為解決是項問題，必須使用稀鬆矩陣(Sparse matrix)處理，以節省時間與空間。spdiags指令則是針對對角元素部份之存取運作，與前面討論之diag之功能可相輔相成。

稀疏對角處埋指令格式如下：


 B = spdiags(A)
 [B,d] = spdiags(A)
 B = spdiags(A,d)
 A = spdiags(B,d,A)
 A = spdiags(B,d,m,n)

spdiags(A)指令以不同的方式處理三個矩陣，可以作為輸入與輸出。其組成係利用不同之輸入參數完成各項功能。其中矩陣Ａ之大小可為mxn，只要陳述非零元素之位址及數值即可，Ｂ則為一輸出項，旨在描述對角線項之陣列，其大小為min(m,n) x p；d則表示矩陣Ａ中非零元素之之對角序列值。

矩陣Ａ中若大小為m x n，則應有m+n-1條對角線。其序列以d參數表示，其範圍為由-m+1至n-1。例如，Ａ之大小為5x6，則應有10條對角線，此10條線分別以d=-4,-3,-2,-1,0,1,2,3,4,5表示。d=0時表示正好在最長的對角線上。其位置可以由下圖表示。

例：


>> e=ones(4,1);A=diag(1:5)+diag(e,1)+diag(e,-1)

A =

    1     1     0     0     0
    1     2     1     0     0
    0     1     3     1     0
    0     0     1     4     1
    0     0     0     1     5

>> [B,d]=spdiags(A)

B =

    1     1     0
    1     2     1
    1     3     1
    1     4     1
    0     5     1


d =

   -1
    0
    1

由結果可知，d指示k值所在，而Ｂ值則是非零對角線上之值，其起點係以左邊項為基準，不足的部份補零。就本例而言第一行為 k=-1，故由基線往右下延伸，不足部分填零；第三行為 k=1，由左邊基線開始，有部份不足，須先補零。這些值可以利用下列指令取得Ｂ中之值列，例如：由矩陣Ａ中取k=1之對角線項值：


>> C=spdiags(A,1)

C =

    0
    1
    1
    1
    1

若要在現有之矩陣增加一對角線項，則可利用 spdiags(B,d,A) 這個指令函數，其中B為填入之值，必須以行的型式，所給的值若超過矩陣Ａ之範圍，則多餘的項會被截斷。d則指示置於那一條對角線上：


>> AA=spdiags([3 4 5]',-3,A)

AA =

  (1,1)        1
  (2,1)        1
  (4,1)        3
  (1,2)        1
  (2,2)        2
  (3,2)        1
  (5,2)        4
  (2,3)        1
  (3,3)        3
  (4,3)        1
  (3,4)        1
  (4,4)        4
  (5,4)        1
  (4,5)        1
  (5,5)        5

>> full(AA)

ans =

    1     1     0     0     0
    1     2     1     0     0
    0     1     3     1     0
    3     0     1     4     1
    0     4     0     1     5

上述指令之應用是在現有之矩陣填入對角線資料，下面的指令spdiags(B,d,m,n)則是創造一個新的稀疏矩陣，其大小為m-by-n。注意陣列Ｂ與d之長度應相符合：


>> B = repmat((1:5)',[1 6])

B =

    1     1     1     1     1     1
    2     2     2     2     2     2
    3     3     3     3     3     3
    4     4     4     4     4     4
    5     5     5     5     5     5

>> d = [-4 -2 -1 0 3 4];
>> A = spdiags(B,d,5,5);
>> full(A)

ans =

    1     0     0     4     5
    1     2     0     0     5
    1     2     3     0     0
    0     2     3     4     0
    1     0     3     4     5

由所得之Ａ矩陣中可知，其大小受m x n之限制，而左下方之排例由B之高項而下，超過者將被截斷。右上方則截斷原需補足的部份，或其尾項由最後項填起。上述之說明實際上僅討論到m=n的情況，實際上當m與n不同時，有些情況因為截斷位置之不同，結果也不一樣。以下面為例：


>> B=reshape(1:15,5,3)

B =

    1     6    11
    2     7    12
    3     8    13
    4     9    14
    5    10    15

>> d=[-2 0 2]

d =

   -2     0     2

>> A=full(spdiags(B,d,5,5))

A =

    6     0    13     0     0
    0     7     0    14     0
    1     0     8     0    15
    0     2     0     9     0
    0     0     3     0    10

當m=n=5時，其填入之順序與前例相同，左下依右邊基準填入，再行截斷；右上則依底部填起，上部截斷。


>> A=full(spdiags(B,d,5,4))

A =

    6     0    13     0
    0     7     0    14
    1     0     8     0
    0     2     0     9
    0     0     3     0

當m＞n時，其左下依右邊基準填入，再行截斷，情況與前例相同；但右上因為截斷的關係，可依k=0處之截斷位置(此處為9倒數第二行)，則依底部填起，此時底部也要截斷一行，再依序往上，截斷超出者。


>> A=full(spdiags(B,d,4,5))

A =

    6     0    11     0     0
    0     7     0    12     0
    3     0     8     0    13
    0     4     0     9     0

當m＜n時，填入之順序相反過來，其左下改依底部往上填入，但依k=0處之截斷位置(此處為9倒數第二行)，則依底部填起，此時底部也要截斷一行，再依序往上，截斷超出者。右上邊則改由上面之基準填入，再依長度進行截斷。此種情況完全與前面之m=n及m＞n之情況相反，須特別注意。

在使用spdiags(A)，取出其對角線值置入Ｂ矩陣時，也有類似情況，當m＜n時，其取出之順序也會相反，例如：

當m=n時：


     Matrix A                        Matrix B

6    0   13    0    0                 1   6   0
0    7    0   14    0                 2   7   0
1    0    8    0   15  == spdiags =>  3   8  13
0    2    0    9    0                 0   9  14
0    0    3    0   10                 0  10  15

當m＞n時：


   Matrix A                     Matrix B

6    0   13    0                 1   6   0
0    7    0   14                 2   7   0
1    0    8    0  == spdiags =>  3   8  13
0    2    0    9                 0   9  14
0    0    3    0

當m＜n時：


     Matrix A                        Matrix B

6    0   11    0    0                 0   6  11
0    7    0   12    0                 0   7  12
3    0    8    0   13  == spdiags =>  3   8  13
0    4    0    9    0                 4   9   0

10.8.4 三維網絡格點Meshgrid

meshgrid指令

建立 X與 Y矩陣，以產生三維空間圖。

語法：


    [X,Y] = meshgrid(x,y)
    [X,Y] = meshgrid(x)
    [X,Y,Z] = meshgrid(x,y,z)

說明

這是一個準備網絡點之事前指令，提供後續指令如mesh、surf指令所需之基本資料。此指令利用獨立之兩維向量 x 與 y，將其轉換為Ｘ與Ｙ之對應網絡座標。其結果是：Ｘ之諸列為x向量之複製；Ｙ值內之行向量則是複製y向量。


>> [X,Y]=meshgrid(3:8,1:6)

X =

   3     4     5     6     7     8
   3     4     5     6     7     8
   3     4     5     6     7     8
   3     4     5     6     7     8
   3     4     5     6     7     8
   3     4     5     6     7     8


Y =

   1     1     1     1     1     1
   2     2     2     2     2     2
   3     3     3     3     3     3
   4     4     4     4     4     4
   5     5     5     5     5     5
   6     6     6     6     6     6

若將Z值作成下列函數關係，例如：


　　z = x e^(-x²-y²)

依據此函數，製成網點後，求得對應z值，並以mesh(z)執行結果如下：


>> [X,Y] = meshgrid(-2:.2:2, -2:.2:2);
>> z=X.*exp(-X.^2-Y.^2);mesh(z)

若輸入參數僅x一項，則其結果與下面之型式相同：

　[X,Y] = meshgrid(x) 與 [X,Y] = meshgrid(x,x)之結果相同。例如：


>> [X,Y]=meshgrid(1:5)

X =

   1     2     3     4     5
   1     2     3     4     5
   1     2     3     4     5
   1     2     3     4     5
   1     2     3     4     5


Y =

   1     1     1     1     1
   2     2     2     2     2
   3     3     3     3     3
   4     4     4     4     4
   5     5     5     5     5

同理，[X,Y,Z] = meshgrid(x,y,z) 是以三維陣列向量輸入，由此計算其相關函數之圖型。

值得注意的是，除meshgrid這個製造網點之指令外，另有一個類似指令稱為ndgrid。兩個指令之功能大致相同，只是其輸入之向量位置對換。因此，下面之指令


    [X,Y,Z] = meshgrid(x,y,z)

其所產生之結果應與下一個ndgrid之指令相同：


    [Y,X,Z] = ndgrid(y,x,z)

只是，meshgrid指令較適合於二維或三維

给我老师的人工智能教程打call！http://blog.csdn.net/jiangjunshow

行列式與反矩陣

特徵值及特徵向量(Eigen Value & Eigen Vector)

左除法求解

反矩陣法求解

程式內容：

範例三：

分析：

程式內容：

穩態熱傳導的問題

程式說明

程式內容

執行例：

範例五：熱流問題

程式內容

執行範例

深入分析

程式內容

det & rank 指令

舉例：

範例：

範例六：

程式內容

pinv指令

rref指令

例題：

梯形數值分析法(Trapezoidal Numerical Integration)

三角形面積

任意形狀之面積

程式內容

程式設計

程式內容

執行範例

程式結構

程式內容

程式內容

diag對角指令

稀疏函數spfun

處理稀疏矩陣之亂數指令sprandn/sprand

轉換用指令spconvert

meshgrid指令

說明

给我老师的人工智能教程打call！http://blog.csdn.net/jiangjunshow

猜你喜欢