机器学习基础概念

1. 输入空间与输出空间

将输入与输出所有可能取值的集合分别称为输入空间与输出空间。

2. 特征空间

以特征向量表示实例，则所有特征向量存在的空间称为特征空间。

3. 联合概率分布

监督学习假设输入输出随机变量 $X$和 $Y$遵循联合概率分布 $P(X, Y)$，训练数据与测试数据视为独立同分布产生。

4. 假设空间

模型属于由输入空间到输出空间的映射的集合，这个集合就是假设空间。
监督学习的模型可以是概率或非概率模型，由条件概率分布 $P(X|Y)$或决策函数 $Y=f(X)$表示。

5. 统计学习三要素

5.1 模型

模型的假设空间包含可能的条件概率分布或决策函数。
假设空间 $\mathcal{F}$定义为决策函数的集合， $X$和 $Y$定义为输入空间 $\mathcal{X}$和输出空间 $\mathcal{Y}$上的变量， $\mathcal{F}$是由参数向量决定的函数族：
$\mathcal{F}=\{f | Y = f_\theta(X), \,\theta \in \R^n\}$

假设空间亦可定义为条件概率的集合：
$\mathcal{F}=\{P | P_{\theta}(Y|X),\,\theta \in \R^n\}$

5.2 策略

考虑按照何种准则学习和选择最优模型，统计学习目标在于从假设空间中选取最优模型。

（1）损失函数和风险函数
用损失函数或代价函数来度量预测误差，损失函数为 $f(X)$和 $Y$的非负实值函数，记为 $L(Y, f(X))$。

常用损失函数有0-1损失函数
$L(Y, f(X) = \begin{cases} 1, &Y \neq f(X) \\ 0, &Y= f(X)\end{cases}$

以及平方损失函数 $L(Y, f(X)) = (Y- f(X))^2$、对数损失函数 $L(Y, P(Y|X)) = -\log P(Y|X)$等。

给定训练集 $T = \{(x_1, y_1), \cdots, (x_N, y_N)\}$，模型 $f(X)$关于训练数据集的平均损失称为经验风险或经验损失，即
$R_{emp}(f) = \frac{1}{N}\sum_{i=1}^N L(y_i, f(x_i))$

由大数定律可知，当样本数趋于无穷时，平均损失趋向于期望损失。但若样本有限，用经验风险估计期望风险并不理想，一般需矫正经验风险，如经验风险最小化和结构风险最小化。

（2）经验风险最小化和结构风险最小化
经验模型最小化
$\min_{f \in \mathcal{F}} \frac{1}{N}\sum_{i= 1}^NL(y_i, f(x_i))$

当模型是条件概率分布，损失函数是对数损失函数，经验风险最小化等价于极大似然估计。

结构风险最小化
当样本容量大小时，经验风险最小化学习未必表现很好，易产生过拟合现象。结构风险最小化可防止过拟合，等级与正则化。
结构风险最小化在经验风险上附加模型复杂度的正则化项，结构风险定义为
$R_{srm}(f) =\frac{1}{N}\sum_{i= 1}^NL(y_i, f(x_i)) + \lambda J(f)$

其中 $J(f)$表示模型复杂度，是定义在假设空间$\mathcal{F}上的泛函。

在系数 $\lambda$一定时，模型 $f$越复杂， $J(f)$越大，即对复杂模型的惩罚越大。 $\lambda$权衡经验风险和模型复杂度，结构风险小的模型对训练数据以及未知测试数据的预测更好。当模型是条件概率分布，损失函数是对数损失函数，模型复杂度由模型的先验概率表示时，结构风险最小化等于与最大后验概率估计。

5.3 算法

算法是指学习模型的具体计算方法，从寻找全局最优、求解过程高效出发。

6. 训练误差与测试误差

目的：使学习到的模型对已知数据和未知数据均具有很好的预测能力。

测试误差是模型 $Y = \hat f(X)$关于测试数据集的平均损失：
$e_{test} = \frac{1}{N'} \sum_{i=1}^{N'}L(y_i, \hat f(x_i))$

当损失函数是0-1损失函数时，测试误差为测试数据集上的误差率（error rate）
$e_{test} = \frac{1}{N'} \sum_{i=1}^{N'}I(y_i \neq \hat f(x_i))$

式中 $I$是指示函数，即 $y \neq \hat f(x)$时为1，否则为0。测试误差反映了模型对未知数据的预测能力，测试误差小的模型具有更好的预测能力，泛化能力更强。

7. 过拟合与模型选择

学习的模型应逼近假设空间中的“真”模型，即模型的参数个数与“真”模型的参数个数尽可能接近。
若模型的复杂度较高（参数过多），模型对训练数据预测较好，但对未知数据预测较差，则这种现象称为过拟合。

$M$次多项式可完全拟合 $M+1$个数据点， $M$次多项式
$f_M(x, w) = w_0 + w_1 x + \cdots + w_Mx_M = \sum_{j=0}^Mw_j x_j$

假设用0~9次多项式函数拟合10个数据，选取平方函数作为损失函数，则
$L(w) = \frac{1}{2}\sum_{i=1}^N (f(x_i, w) - y_i)^2$

可使用最小二乘求解出多项式系数的唯一解，假设当 $M=10$时，模型对测试数据的拟合效果很好，但由于数据本身存在噪声，复杂的模型对未知数据的预测能力表现很差，如下图：

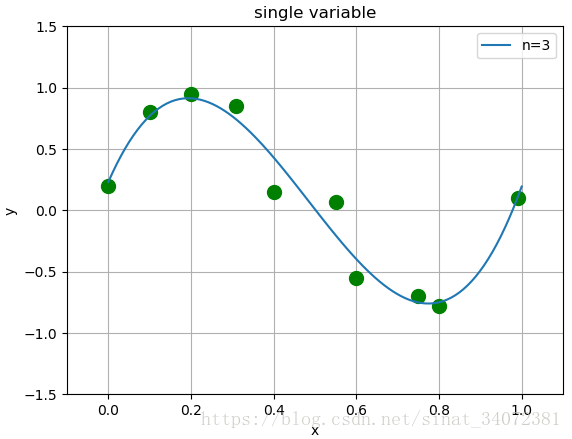
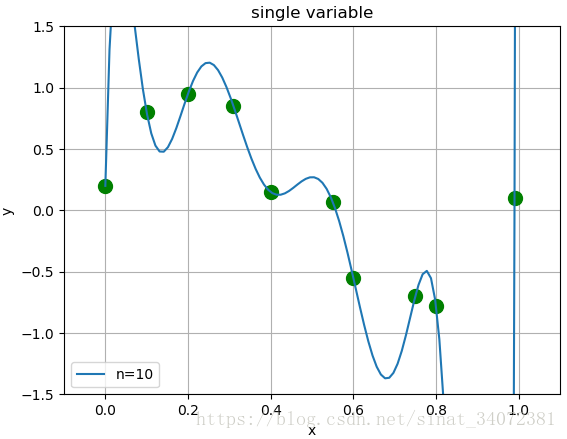
图1 不同模型复杂度下的拟合效果
随着模型复杂度的增加，训练误差减小，直至趋于0。但测试误差一般会随着模型复杂度的增加先减小后增大。 图2 训练误差和测试误差与模型复杂度的关系

8. 正则化

正则化（regularization）用于模型选择，是结构风险最下化策略的实现。正则项一般是模型复杂度的单调递增函数，如正则化可以是模型参数向量的范数。
$\min_{f \in \mathcal{F}} = \frac{1}{N} \sum_{i=1}^N L(y_i, f(x_i)) + \lambda J(f)$

如回归问题中，损失函数是平方的损失，正则化可以是参数向量 $L_1$或 $L_2$范数，即 $J(f)=||w||_1$或 $J(f)=||w||^2/2$。
经验风险较小的模型可能较复杂（含多个非零参数），此时正则项较大，正则化的作用是选择经验风险和模型复杂度同时较小的模型。

9. 交叉验证

若样本数据充足，可简单地将数据集随机切分为训练集、验证集和测试集。训练集用于模型训练，验证集用于模型选择，测试集用于模型评估。对于不同复杂度的模型，应选择对验证集有最小预测误差的模型。若样本集较小，考虑采用交叉验证方法选择模型。

9.1 简单交叉验证

随机地将数据分为训练集和测试集，如70%数据为训练集、30%数据为测试集。
用训练集在各种条件下（不同参数个数）训练模型，得到多个不同的模型，在各模型中选择对测试集有最小预测误差的模型。

9.2 $\mathcal{S}$折交叉验证

随机地将已给数据集切分为 $\mathcal{S}$各互不相交且大小相同的子集，利用 $\mathcal{S}-1$个子集的数据训练模型，利用剩下的子集测试模型。对每一个模型重复上述过程 $\mathcal{S}$次，记录平均测试误差，最后选取所有模型中平均测试误差最小的模型。

9.3 留一交叉验证

留一交叉验证是 $\mathcal{S}$折交叉验证的特殊情形，每次仅留一个样本作为测试集，即 $\mathcal{S}=N$（ $N$为数据集容量）。
留一计算繁琐，样本利用率高，适合于小样本训练。

10. 泛化能力

模型的泛化能力是指模型对未知数据的预测能力。模型对未知数据预测的误差，即泛化误差（期望风险），定义为
$R_{\tt{exp}}(\hat{f}) = E_P[L(Y, \hat f(X))] = \int_{\mathcal{X\times Y}}L(y, \hat f(x))P(x, y) dxdy$

一般通过模型的泛化误差上界来评估各模型的泛化能力。

考虑二分类问题，数据集 $T=\{(x_1, y_1), \cdots, (x_N, y_N) \}$，各样本独立同分布，类别 $Y \in \{-1, +1\}$，假设空间为函数的有限集合 $\mathcal{F} = \{f_1, \cdots, f_d\}$，损失函数为0-1损失，则 $f$的期望风险和经验风险分别为
$R(f) = E[L(Y, f(X))] \\ \,\\ \hat R(f) = \frac{1}{N} \sum_{i=1}^N L(y_i, f(x_i))$

其中经验风险最小化函数为 $f_N = \arg \min_{f \in \mathcal{F}}\hat R(f)$，则 $f_N$的泛化能力 $R(f_N) = E[L(Y, f_N(X))]$。

对于二分类问题，假设空间 $\mathcal{F} = \{f_1, \cdots, f_d\}$，对于任意 $f\in \mathcal{F}$，至少以概率 $1- \delta$，使得不等式成立

$R(f) \leq \hat R(f) + \sqrt{\frac{1}{2N}(\log d - \log \delta)}$

其中不等式右项为泛化误差上界。其中第一项为训练误差，训练误差约大，泛化误差越大。第二项是 $N$的单调递减函数， $N$趋于无穷时，该项趋于0。同时第二项也是 $\sqrt{\log d}$阶函数， $d$越大，假设空间 $\mathcal{F}$所含函数越多，该项值越大。

证明：
设 $S_n = \sum_{i=1}^nX_i$是独立随机变量 $X_1, \cdots, X_n$之和， $X_i \in [a_i, b_i]$，对于任意 $t>0$，由Hoeffding不等式知
$P(ES_n - S_n \geq t) \leq \exp\left(\frac{-2t^2}{\sum_{i=1}^n(b_i-a_i)^2} \right)$

对任意函数 $f\in \mathcal{F}$， $\hat R(f)$和 $R(f)$分别是 $N$个独立随机变量 $L(Y, f(X))$的样本均值和期望。若损失函数是0-1损失，对于 $\epsilon>0$，则
$P(R(f) - \hat R(f) \geq \epsilon) \leq \exp(-2N\epsilon^2)$

因此
$\begin{aligned} P( \exists f \in \mathcal{F} : R(f) - \hat R(f) \geq \epsilon) & = p(\bigcup_{ f \in \mathcal{F}}\{R(f) - \hat R(f) \geq \epsilon\}) \\ & \leq \sum_{ f \in \mathcal{F}}P(R(f) - \hat R(f) \geq \epsilon) \\ & \leq d \exp(-2N \epsilon^2) \end{aligned}$

即对于任意 $f \in \mathcal{F}$，有
$P(R(f) - \hat R(f) < \epsilon) \geq 1- d \exp(-2N \epsilon^2)$

令 $\delta = d \exp(-2N \epsilon^2)$，则
$P(R(f)< \hat R(f) + \epsilon) \geq 1- \delta$

即至少以概率 $1- \delta$认为 $R(f)< \hat R(f) + \epsilon$。

11. 生成模型与判别模型

生成模型
由数据学习联合概率分布 $P(X, Y)$，然后求出条件概率分布 $P(Y|X)$作为预测模型，即生成模型 $P(Y|X) = P(X, Y)/P(X)$。

为什么叫做生成模型？
模型表示了给定输入 $X$产生输出 $Y$的生成关系，典型的生成模型有隐马尔可夫模型和朴素贝叶斯方法。

生成模型特点

• 可还原输入输出的联合概率分布 $P(X, Y)$;
• 当样本数增加时，生成模型可更快收敛；
• 存在隐变量时，只能使用生成模型；

判别模型
由数据直接学习决策函数 $f(X)$或条件概率分布 $P(Y|X)$作为预测模型，即判别模型。

为什么叫做判别模型？
模型表示了给定输出 $X$时，应该预测什么样的输出 $Y$，典型的判别模型有决策树、逻辑回归、支持向量机等。

判别模型特点

• 直接学习条件概率分布 $P(Y|X)$或决策函数$f(X)，预测准确率更高；
• 可对数据的特征进行抽象，学习问题得到简化；

12. 分类问题

在监督学习中，输出变量 $Y$取有限个离散值时，预测问题为分类问题。

对于二分类问题，分类器在测试集上预测结果有4种情况，如下：

查准率/精准率
$P = TP/(TP + FP)$，表示真实正例占预测正例的比例。

召回率
$R = TP / (TP + FN)$，表示真实正例被正确预测的比例。

F1值
$2/F_1 = 1/P + 1/R$，表示查准率与召回率的调和均值。当 $P$和 $R$均较高时， $F_1$也较高。

13. 标注问题

根据输入的观测序列 $X$，预测输出的标记序列或状态序列 $Y$。模型可表示为条件概率分布，即
$P(Y^{(1)}, \cdots, Y^{(n)}|X^{(1)}, \cdots, X^{(n)})$

具体地，对于观测序列 $x_{N+1} = (x_{N+1}^{(1)}, \cdots, x_{N+1}^{(n)})^T$，找到使条件概率 $P((y_{N+1}^{(1)}, \cdots, y_{N+1}^{(n)})^T|(x_{N+1}^{(1)}, \cdots, x_{N+1}^{(n)})^T)$最大的标记序列 $y_{N+1} = (y_{N+1}^{(1)}, \cdots, y_{N+1}^{(n)})^T$。常见的标注统计学习方法有隐马尔可夫模型、条件随机场。

14. 回归问题

回归问题等价于函数拟合，即选择一条函数曲线使其很好地拟合已知与未知数据。模型可表示为函数隐射，即
$Y = f(X)$