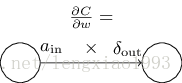TensorFlow官方教程《Neural Networks and Deep Learning》译（第二章）

反向传播算法（BackPropagation algorithm）的工作原理

在上一章节中，我们看到了神经网络是如何利用梯度下降算法从数据中学习权重值 weights 和偏倚量值 biases ，完成“学习” 的过程。但是，在算法原理的解释中，有一个环节被跳过了：我们没有讨论如何计算成本函数（cost function）的梯度值。这是很重要的一个环节！在这一章，我们会解释一个快速计算这种梯度的算法，名为“反向传播算法”（BackPropagation algorithm）。

反向传播算法原本是 19世纪70年代提出的，但是其重要性直到 1986 年的一篇由（David Rumelhart ， Geoffrey Hinton, Ronald Williams 三人所写的一篇著名论文发布以后才真正被世人意识到。这篇论文描述了几个神经网络在使用了反向传播算法以后，学习速度比之前有显著提升，使得用这些神经网络来解决以前看上去不可解的问题成为可能。如今，反向传播算法已经成为了神经网络进行学习的“核心骨干”算法。

本章节与本书的其余章节相比涉及了更多数学上的内容。如果你对数学不是很热衷，你可能会想要跳过这一章节，然后把反向传播算法当做一个忽略其内部细节的黑盒来使用。但是为什么我们要花费时间来学习这些细节呢？

原因当然是为了“弄懂”。 反向传播算法 核心是一个成本函数 $C$ 对于神经网络的任意一个权重 w( 或者偏倚量 b) 求偏导的表达式 $\frac{\partial C}{\partial w}$ 。这个表达式可以告诉我们当改变权重 weights 和偏倚量 biases 时，随之引发的成本函数值的变化程度。虽然这个表达式有点复杂，但是它也有非常优雅的地方，其中的每一个元素都有一个非常自然，符合第一直觉的解释。所以，反向传播算法不仅仅是一个用于神经网络学习的快速算法，它还能告诉我们权重和偏倚量的更改是如何影响神经网络的整体行为。所以，它值得我们深入细节进行学习。

虽然说了上面这一大堆，如果你依旧只是想略读这一章，或是直接跳过这一章，也是ok的。本书的其余章节在写作时，已经考虑到了你有可能跳过本章，直接将反向传播算法当做一个黑盒的情况。所以即使你不略过了本章，你依旧可以理解后续章节的主要结论，尽管你可能无法完全跟的上其中的推导过程。

热身：一个快速的基于矩阵计算神经网络输出的方法

在讨论反向传播算法前，让我用一个基于矩阵计算神将网络输出的算法热个身。事实上，在上一章结尾，我们已经初步见识过这一算法了，但是当时我快速的一带而过了，所以值得再重新探究一下其中的细节。这是一个让我们逐渐熟悉反向传播算法中所使用数学记号的很好的方式。

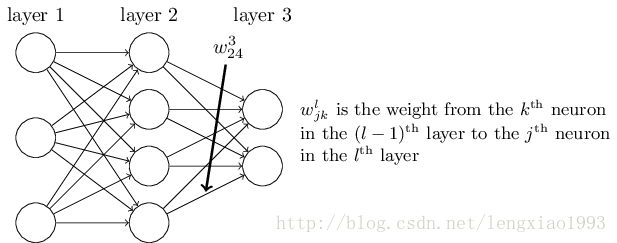
让我们从一个让人感到含糊不清的指代神经网络众多权重的记号开始。我们会用 $w^l_{jk}$ 来表示 $（l-1）$ 层第 $k$ 个神经元到 $l$ 层的第 $j$ 个神经元之间连接的权重值。例如，如下图所示，第2 层的第 4 个神经元到第3层的第 2 个神经元之间的连接权重是 $w^3_{24}$ ：

这里写图片描述

这个记号乍一看是让人很不习惯的，它确实需要花费一些功夫来掌握。但是经过较小的努力之后，你会发现这个记号变得简单和自然起来。这个记号的一个古怪之处在于 $j$ 和 $k$ 的排列顺序。你可能会想，用 $j$ 来指代输入神经元的位置， $k$ 来指代输出神经元的位置不是更合理吗？之后我会解释这个古怪之处的原因。

我们使用一个类似的记号来表示神经网络的偏倚量（biases）和激活结果( activations) 。我们用 $b^l_j$ 来表示第 $l$ 层的第 $j$ 个神经元的偏倚量，用 $a^l_j$ 来表示第 $l$ 层的第 $j$ 个神经元的偏倚量的激活结果，下图是这两个记号使用方式的示意图：

这里写图片描述

利用这些记号，第 $l$ 层的第 $j$ 个激活结果 $a^l_j$ 和第 $(l-1)$ 层的激活结果 $a^l_j$ 就可以通过下面的等式关联起来（读者可以把这个等式和我们上一个章节的等式【4】比较一下）：

a l j = σ (\sum k w l j k a l - 1 k + b l j), (23)

$\begin{eqnarray} a^{l}_j = \sigma\left( \sum_k w^{l}_{jk} a^{l-1}_k + b^l_j \right), \tag{23}\end{eqnarray}$

上面等式中的 $\sum_k w^{l}_{jk} a^{l-1}_k$ 是对 $l-1$ 层所有（一共 k 个）神经元的加权输入求和。为了把上面这个等式重写为矩阵计算的形式，我们为每一个 $l$ 层神经元定义一个权重矩阵 $w^l$ 。权重矩阵 $w^l$ 中的每一个元素就是连接到第 l 层神经元的权重值，也就是说，矩阵中第 j 行，第k 列的元素就是 $w^l_{jk}$ 。类似的，我们为每一个 $l$ 层神经元定义一个便宜向量 $b^l$ , 该向量中的第 j 个元素就是 $b^l_j$ 。类似的，我们再定义一个激活结果向量 $a^l$ , 该向量中的第 j 个元素就是 $a^l_j$

等式（23）中最后一个需要重写的部分就是把 $\sigma$ 函数向量化。我们在上一个章节中已经初步见识过如何进行向量化，但是为了复习加深印象，这里来重述一下，核心思想是，我们想对向量中 $v$ 的每一个元素应用函数 $\sigma$ 。我们用一个非常直观的记号 $\sigma（v）$ 来表示一个函数对于向量上的以元素为单位进行的计算。也就是说 $\sigma（v）$ 中的元素的计算方式就简单是： $\sigma（v）_j =\sigma（v_j）$ 。举例来说，如果我们有一个函数 $f(x) = x^2$ , 那么，它向量化的表示形式的运算过程就是：

f ([23]) = [f (2) f (3)] = [49], (24)

$\begin{eqnarray} f\left(\left[ \begin{array}{c} 2 \\ 3 \end{array} \right] \right) = \left[ \begin{array}{c} f(2) \\ f(3) \end{array} \right] = \left[ \begin{array}{c} 4 \\ 9 \end{array} \right], \tag{24}\end{eqnarray}$

向量化后的 $f$ 其实就是对向量中的每个元素应用 $f$ 进行平方计算。

有了这些记号，等式（23）就可以被重写为非常漂亮可以被重写为漂亮且紧凑的向量形式：

a l = σ (w l a l - 1 + b l) . (25)

$\begin{eqnarray} a^{l} = \sigma(w^l a^{l-1}+b^l). \tag{25}\end{eqnarray}$

这个表达式给了我们一个从全局角度思考一层神经元的激活结果是如何与前一层神经元的激活结果进行关联的：* 在激活结果上乘以权重矩阵，然后与偏倚量向量相加，然后再应用 $\sigma$ 函数。

*注释： $w^l_{jk}$ 记号的奇怪之处的作用在这里体现，如果我们用 j 了表示输入神经元的位置，用 k 表示输出神经元的位置，那么我们就不得不把表达式（25）中的权重矩阵 $w^l$ 替换为它的转置矩阵。这是一个很小的改变，但是这样做之后，就不能直接说”在激活结果上乘以权重矩阵”

这种全局的视角与之前以神经元为单位的思考更简单，更精炼（同时涉及到更少的上下标）。把它当做是一种避免繁琐上下标，且不失准确性的表达技巧。这种表达式在实践中也很有用，因为大部分的矩阵运算库提供了矩阵乘法，向量加法，向量化的快速实现方法。事实上，上一章节的代码
已经隐含地使用了上面那个表达式来计算神经网络的行为。

在使用表达式【25】来计算 $a^l$ 时，我们计算了中间量 $z^l \equiv w^l a^{l-1}+b^l$ 。这个量会变成一个非常有用，值得被命名的变量：我们把 $z^l$ 称为 $l$ 层的权重化输入（weighted input），在之后的章节里我们会对权重化输入进行细致地使用。表达式（25）有时会被写作权重输入的形式，即 $a^l = \sigma(z^l)$ 。很自然的， $z^l$ 的元素 $z^l_j = \sum_k w^l_{jk} a^{l-1}_k+b^l_j$ , 也就是说， $z^l_j$ 就是第 $l$ 层第 $j$ 个神经元的激活函数的输入。

两个我们所需的关于成本函数的假设

反向传播函数的目标是计算成本函数 $C$ 关于神经网络中任意的权重 w 或偏倚量 b 的偏导数 $\frac{\partial C}{ \partial w}$ 和 $\frac{\partial C}{ \partial b} 。为了使得反向传播函数工作，我们需要针对成本函数的形式做两个假设。但是在陈述这些假设之前，先在脑中建立起一个样例的成本函数会很有用。

我们会使用上一张提到的二次成本函数作为示例（等式【6】）。在上一节的记号中，二次成本函数有如下的形式：

C = 1 2 n \sum x ∥ y (x) - a L (x) ∥ 2, (26)

$\begin{eqnarray} C = \frac{1}{2n} \sum_x \|y(x)-a^L(x)\|^2, \tag{26}\end{eqnarray}$

其中： $n$ 是训练输入的总数；求和 $y=y(x)$ 是每一个训练输入 $x$ 所期待的输出。 L 表示神经网络的层数； $a^L = a^L(x)$ 是当 $x$ 被输入后，激活结果向量的输出。

好的，那么我们为了成本函数 $C$ 得以使用所需要作的假设是什么呢？我们所需要的第一个假设是成本函数可以被写成平均值形式 $C = \frac{1}{n} \sum_x C_x$ 。这是二次成本函数的例子，其中，对于单个的输入，成本函数结果 $C_x = \frac{1}{2} |y-a^L |^2$ 。这个结果对于本书中其他所有的成本函数也是成立的。

我们之所以需要这个假设，是因为反向传播让我们做的实际上是计算单个输入的偏导数 $\frac{\partial C_x}{ \partial w}$ 和 $\frac{\partial C_x}{ \partial b}。然后基于所有训练输入的成本函数结果计算平均值，我们获得了$ \frac{\partial C}{ \partial w} $和$ \frac{\partial C}{ \partial b} $。事实上，脑中有了这个假设以后，我们可以假定所有的输入值是固定的，然后丢掉下标$ x $，把成本$ C_x $写作$ C $. 最后我们会把$ x $放回来，但是目前，这个$ x$ 是一个最好被略去的繁琐记号。

我们所需要做的第二个假设是，成本可以被写作神经网络输出的一个函数计算结果：
这里写图片描述

例如，二次成本函数就满足这个要求，因为单个输入 $x$ 的二次成本函数可以被写成：

C = 1 2 ∥ y - a L ∥ 2 = 1 2 \sum j (y j - a L j) 2, (27)

$\begin{eqnarray} C = \frac{1}{2} \|y-a^L\|^2 = \frac{1}{2} \sum_j (y_j-a^L_j)^2, \tag{27}\end{eqnarray}$

而且因此，也就是激活结果输出的一个函数。当然，这个成本函数的结果也取决于目标输出 $y$ , 你可能在想，为什么我们不把成本函数也当做是 $y$ 的函数。然而这里需要记住的是，一旦训练输入 $x$ 被固定了以后，目标输出 $y$ 也就成为了一个固定的参数。特别是， $x$ 和 $y$ 的值无法通过通过调整权重和偏倚量而产生任何影响，换句话说，它们不是某种神经网络需要学习的东西。因此，把成本 $C$ 仅仅看作是激活结果 $a^L$ 的函数就合情合理了, 其中 $y$ 仅仅是辅助定义函数的一个参数而已。

Hadmard 积， $s \odot t$

f反向传播算法是基于常见的线性代数运算的- 如向量加法，向量与矩阵的乘法等等。但是，有一个运算符没有那么常见。具体而言，假设 $s$ 和 $t$ 是两个维度相同的向量。然后我们使用 $s \odot t$ 来表示两个向量按元素相乘。因此， $s \odot t$
的内容就是 $s （\odot t）_j = s_jt_j$ 。举个例子如下：

[12] ⊙ [34] = [1 * 3 2 * 4] = [38] . (28)

$\begin{eqnarray} \left[\begin{array}{c} 1 \\ 2 \end{array}\right] \odot \left[\begin{array}{c} 3 \\ 4\end{array} \right] = \left[ \begin{array}{c} 1 * 3 \\ 2 * 4 \end{array} \right] = \left[ \begin{array}{c} 3 \\ 8 \end{array} \right]. \tag{28}\end{eqnarray}$

这种按元素相乘的乘法有时被称为 Hadmard(哈达玛达 )乘积或是 Schur 积，这个运算符在实现反向传播算法时会显得很好用。

反向传播算法背后的四个基本等式

反向传播算法帮我们理解神经网络中权重和偏倚量的变动是如何影响成本函数结果变化的。最终，是通过计算偏导数 $\partial C / \partial w^l_{jk}$ 和 $\partial C / \partial b^l_{j}$ 实现的。但是为了计算这些偏导数值，我们首先需要引入一个中间量， $\delta^l_j$ ，我们将这个中间量称为第 $l$ 层第 $j$ 个神经元的误差（error）。反向传播算法会给我们一个计算误差值 $\delta^l_j$ 的步骤，然后把 $\delta^l_j$ 与 $\partial C / \partial w^l_{jk}$ 和 $\partial C / \partial b^l_{j}$ 关联起来。

为了理解这个偏差值是如何被定义的，先想象我们的神经网络中有一个恶魔：

这里写图片描述

这个小恶魔坐在第 $l$ 层的第 $j$ 个神经元。当这个神经元的输入进来的时候，这个小恶魔对神经元的操作进行扰乱。它对神经元的权重化后的输入加上一个微小的改变量 $\Delta z^l_j$ ，使得输出从原本的 $\sigma(z^l_j)$ 变成 $\sigma(z^l_j+\Delta z^l_j)$ 。这个改变会沿着后面的神经网络层进行扩散，直到导致神经网络的总体成本值改变 $\frac{\partial C}{\partial z^l_j} \Delta z^l_j$
。

译者注：最后的这个改变量是一个偏微分表达式，忘记的同学可以复习一下大学课本。

现在这个恶魔变成了一个好的恶魔，并且试图帮助你来改善成本值，也就是说，他们将试着找到一个 $\Delta z^l_j$ ，使得成本值更小。假设 $\frac{\partial C}{\partial z^l_j}$ 有一个较大的绝对值（要么为正值，要么为负值）。这个恶魔可以通过选择一个 $\Delta z^l_j$ 使得其值与 $\frac{\partial C}{\partial z^l_j}$ 符号相反，使得神经网络的成本值降低很多。相反，如果 $\frac{\partial C}{\partial z^l_j}$ 的值很接近于0，那么小恶魔就没有办法通过调整 $\Delta z^l_j$ 来降低（优化）神经网络的成本值。此时，小恶魔就可以说，这个神经元已经非常接近于“最优”了。因此，这里就有了一个直觉性的感受， $\frac{\partial C}{\partial z^l_j}$ 是一种对于神经元偏差的度量。

受到这个故事的启发，我们定义第 $l$ 层第 $j$ 个神经元的误差 $\delta^l_j$ 为：

δ l j \equiv \partial C \partial z l j . (29)

$\begin{eqnarray} \delta^l_j \equiv \frac{\partial C}{\partial z^l_j}. \tag{29}\end{eqnarray}$

按照我们的惯例，我们用 $\delta^l$ 来表示第 $l$ 层神经元的误差所组成的误差向量。反向传播算法给我们提供了一种计算每一层神经元 $\delta^l$ 的方法，然后把这些误差值和我们真正关心的量 $\partial C / \partial w^l_{jk}$ $\partial C / \partial b^l_j$ 关联起来 .

你可能在想，为什么小恶魔会更改权重化输入 $z^l_j$ , 想象小恶魔更改神经元的激活输出 $a^l_j$ ，然后用 $\frac{\partial C}{\partial a^l_j}$ 作为误差的度量不是更自然吗。的确，如果你这样做的话，结果和我们之前的讨论差不多，一样可行，但那时这回使得反向传播算法的代数表达式更加复杂一点。所以我们坚持使用 $\delta^l_j = \frac{\partial C}{\partial z^l_j}$ 作为【误差】的度量。

【】注释：在类似 MNIST 类似的分类问题中，术语 “误差”有时被用来表示分类失败率。例如，如果神经网络正确的识别了 96%的数字，那么误差就是 4% 。显示这和我们的误差向量 $delta$ 的含义是很不一样的，在实践中，你应该可以很轻易地分辨哪一个含义才是应该被使用的才对。

攻击计划：反向传播算法是基于 4 个基础等式。这些等式合起来给了我们一个计算误差 $\delta ^l$ 和成本函数梯度的方法。我会在下面列出这四个等式。不过，请不要期待你能立刻理解这四个等式，这种期待会带来失望。事实上，反向传播算法的这四个基础等式内含极其丰富，以至于仅仅是理解他们就需要花费大量的时间和耐心去慢慢钻研。好消息是，这种耐心会得到很多倍的回报。所以，这一小节的讨论仅仅是个开始，帮助你走上彻底理解等式的道路。

这里先预览一下我们在本章后面的部分将要深入钻研方程的路线：我会给一个等式的简短证明，以解释这些等式为什么成立；我会将这些等式以伪代码的算法形式再次列出，看这些伪代码如何被实现为真正的，可运行的 python 代码。然后，在这一章的最后一节，我会构建一个反向传播算法等式含义的直觉图，以及一个怎样能够从无到有的发现这个等式。沿着这条路线，我们将会反复地审视这四个基础等式，而你会不断加深对它们的理解，最终你会熟悉习惯这四个等式，甚至可能发觉这四个等式是漂亮且自然的。

首先是一个关于输出层误差量的等式 $\delta^l$ :

δ L j = \partial C \partial a L j σ' (z L j) . (BP1)

$\begin{eqnarray} \delta^L_j = \frac{\partial C}{\partial a^L_j} \sigma'(z^L_j). \tag{BP1}\end{eqnarray}$

这是一个非常自然的等式，等式右侧的 $\frac{\partial C}{\partial a^L_j}$ , 仅仅是度量了把成本函数当做是第 $j$ 个激活输出的函数时，成本的变化速度。如果，成本的变化对于特定的输出神经元 $j$ 并没有很明显的依赖，那么 $\delta^L_j$ 就应该是一个较小的值，这也是我们所期望达到的。等式右侧的另一部分 $\sigma'(z^L_j)$ , 度量了激活函数相对于 $z^L_j$ 的改变速率。

注意到 (BP1 ) 中的每个部分都是易于计算的。具体来说，我们在计算神经网络的行为时，会计算 $z^L_j$ ，然后只需要再多花一点开销，就可以计算出 $\sigma'(z^L_j)$ 。当然， $\frac{\partial C}{\partial a^L_j}$ 的实际形式取决于成本函数的形式。然而，如果假设成本函数是已知的，那么计算 $\frac{\partial C}{\partial a^L_j}$ 应该不会太困难。例如，如果我们用二次成本函数， $C = \frac{1}{2} \sum_j (y_j-a^L_j)^2$ , 那么， $\partial C / \partial a^L_j = (a_j^L-y_j)$ 就，这显然是很容易计算的。

译者注：又需要复习一下高数里的微分部分。

等式 （BP1） 是一个关于 $\delta^L_j$ 分量化（被表达成两个部分的量相乘）的表达式。他是一个极其好的表达式，但是不是我们想要的，矩阵形式的表达式。然而，把它重写成矩阵式的表达式是很容易的，如下

δ L = \nabla a C ⊙ σ' (z L) . (BP1a)

$\begin{eqnarray} \delta^L = \nabla_a C \odot \sigma'(z^L). \tag{BP1a}\end{eqnarray}$

这里， $nabla_a C$ 被定义为一个元素为偏导数 $\partial C / \partial a^L_j$ 的向量。你可以把 $nabla_a C$ 想作为成本函数 $C$ 的关于输出激活量的变化率的表示。很容易看到，等式（BP1a）和 $BP1$ 是等价的，因此我们会用 $BP1$ 来统一带只这两个表达式。例如，在二次成本函数的例子中，我们有 $\nabla_a C = (a^L-y)$ , 那么（BP1）完整的表达式的形式就是：

δ L = (a L - y) ⊙ σ' (z L) . (30)

$\begin{eqnarray} \delta^L = (a^L-y) \odot \sigma'(z^L). \tag{30}\end{eqnarray}$

如你所见，这个表达式中的每个部分都有一个非常简洁的向量形式，而且很容易使用类似 Numpy 的库进行计算。

等式 （BP2） 是是关于误差量 $\delta^l$ 下一层误差量 $\delta^（l+1）$ 的等式：

δ l = ((w l + 1) T δ l + 1) ⊙ σ' (z l), (BP2)

$\begin{eqnarray} \delta^l = ((w^{l+1})^T \delta^{l+1}) \odot \sigma'(z^l), \tag{BP2}\end{eqnarray}$

其中， $(w^{l+1})^T$ 是 $（l+1）$ 层神经元的权重矩阵的转置。这个等式似乎比较复杂，但是每个元素都有一个很好的解释。假设我们知道 $l+1$ 层的误差 $\delta^{l+1}$ ，当 $(w^{l+1})^T$ 与 $\delta^{l+1}$ 矩阵相乘后，我们可以将其直觉化地想象成把误差量沿着神经网络反向移动了一层，给我们提供了测量 $l$ 层神经元输出的误差量的手段。

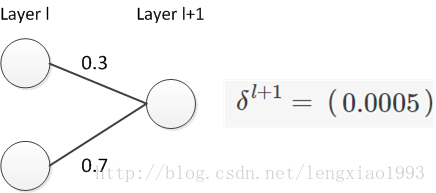
译者注：这里补充一个例子，来说明为什么是反向移动了一层。

这里写图片描述

下面假设我们有一个神经网络结构， $l+1$ 层的神经元只有一个， $l$ 层神经元有两个，且连接到 $l+1$ 层的权重如图所示为 0.3 和 0.7，那么套用上面的公式，则有如下的结果

δ l + 1 = (0.0005)

$\delta^{l+1} = \left(\begin{array}{c} 0.0005 \end{array}\right)$

(w l + 1) T = (0.3 0.7)

$(w^{l+1})^T = \left(\begin{array}{c} 0.3\\0.7 \end{array}\right)$

(w l + 1) T \cdot δ l + 1 = (0.3 0.7) (0.0005) = (0.3 * 0.0005, 0.7 * 0.0005)

$(w^{l+1})^T \cdot \delta^{l+1} =\left(\begin{array}{c} 0.3\\0.7 \end{array}\right) \left(\begin{array}{c} 0.0005 \end{array}\right) = \left(\begin{array}{c} 0.3 * 0.0005, 0.7 * 0.0005 \end{array}\right)$

从上例可以看出， $l+1$ 层的权重在如上公式作用下，被反向分解到了前一层，看起来就像是把误差向前移动了一层一样。

然后我们把误差反向移动后的结果与 $\sigma'(z^l)$ 作 Hadamard 乘积，即 $\odot \sigma'(z^l)$ 。这一操作把误差继续反向移动，穿过了 $l$ 层的激活函数，给我们提供了 $l$ 层神经元权重化后的输入的误差量。

通过合并（BP_2） 和 （BP_1） 两个等式，我们可以计算出任意一层的误差量。我们可以先用（BP_1） 算出 $\delta^L$ , 然后应用 BP_2 来计算 $\delta^{L-1}$ ，然后再应用 $BP_2$ 来计算 $\delta^{L-2}$ ，以此类推，一直反向计算下去。

等式（BP3） 是一个以神经网络中任意偏倚量为参照的成本函数改变速率有关的等式：

\partial C \partial b l j = δ l j . (BP3)

$\begin{eqnarray} \frac{\partial C}{\partial b^l_j} = \delta^l_j. \tag{BP3}\end{eqnarray}$

这个等式说明，偏差量 $\delta^l_j$ 恰好就等于成本函数相对偏倚量的变化率 $\frac{\partial C}{\partial b^l_j}$ 。这是一个非常重大的好消息，因为 （BP_1） 和 （BP_2） 已经告诉我们如何计算 $\delta^l_j$ 。我们可以把（BP_3） 重新简写为：

\partial C \partial b = δ, (31)

$\begin{eqnarray} \frac{\partial C}{\partial b} = \delta, \tag{31}\end{eqnarray}$

等式中，误差 $\delta$ 和偏倚量 $b$ 都是针对同一神经元。

等式（BP4） 是一个以神经网络中任意权重为参照是成本函数的改变速率相关的等式：

\partial C \partial w l j k = a l - 1 k δ l j . (BP4)

$\begin{eqnarray} \frac{\partial C}{\partial w^l_{jk}} = a^{l-1}_k \delta^l_j. \tag{BP4}\end{eqnarray}$

这个等式告诉我们如何利用我们已经知道怎么计算的 $\delta^l$ 和 $a^{l-1}$ 进一步计算偏导数 $\partial C / \partial w^l_{jk}$ 。这个等式可以被进一步简写为上下标比较简洁的形式：

\partial C \partial w = a i n δ o u t, (32)

$\begin{eqnarray} \frac{\partial C}{\partial w} = a_{\rm in} \delta_{\rm out}, \tag{32}\end{eqnarray}$

这个等式中， $a_{\rm in}$ 是两个神经元连接权重 $w$ 上输入端神经元的激活量， $\delta_{\rm out}$ 是权重 $w$ 输出端神经元的误差量。通过图片放大来看就是如下的情况：
这里写图片描述

等式 （32） 有一个很好的推论是，当激活量 $a_{\rm in}$ 很小时，即 $a_{\rm in} \approx 0$ ，梯度 $\partial C / \partial w$ 也会变得很小。这种情形下，我们会说，权重学习得较为缓慢，因为权重在梯度下降的过程中，并没有改变很多，换句话说， 等式（BP4） 的结论是，激活量较低的神经元对应的权重输出的学习会较为缓慢。

沿着这四大基本方程，很有很多其他的结论。然我们从输出层开始，考虑等式（BP1）中的 $\sigma'(z^L_j)$ 项。回想一下上一章的 S形函数。

这里写图片描述

当 $\sigma(z^L_j)$ 的值接近于 0 或是 1 时，函数曲线变得非常平，这种情况下， $\sigma'(z^L_j) \approx 0$ 。所以，我们可以从中看出，如果输出神经元的处于低激活状态（ $\approx 0$ ）或高激活态（ $\approx 0$ ）最后一层的权重会学习得较为缓慢。我们通常将这种情形称为 “输出神经元饱和”，其结果是，相对应的权重已经停止了学习（或者说学习得非常缓慢）。类似的说法，对输出神经元的偏倚量也是成立的

从前面的神经元层中，我们也可以获得类似的见解。具体来说，可以注意观察一下 等式(BP2)中的 $\sigma'(z^l)$ 。从这个等式中我们可以看出，当一个神经元接近饱和， $\sigma'(z^L_j) \approx 0$ 时，误差量 $\delta^l_j$ 有可能会变得很小。这样，反过来也意味着一个即将饱和的权重输入学习的很慢。 *

注：之所以说有可能会变小，是因为考虑到 $((w^{l+1})^T \delta^{l+1})$ 这个向量中有可能会包含非常大的项，以此抵消了较小的 $\sigma'(z^l)$ 的影响。这里主要是在描述变化的趋势。

总结一下，我们从之前的分析中了解到，无论是输入神经元处于低激活态或是输出神经元处于饱和态（低激活态或高激活态），一个权重的学习过程都会变缓慢。

这些发现都没什么让人感到惊讶的地方。他们依旧只是帮我们改善我们头脑里神经网络的模型，以更好地理解神经网络是如何学习的。进一步，我们可以把这类的推理进行推广。之前列出的四个基本等式不仅针对标准的 S型函数成立，对任意类型的激活函数也是成立的（这是因为，等式的证明过程中没有使用任何独属于 S型函数的特殊性质，这个证明过程我们之后会看到）。因此我们可以使用这些等式来设计一些具备我们所期待性质的激活函数。下面通过一个例子来进行说明，假设我们选择了一个（非S型）激活函数 $\sigma()$ ，该函数的导数函数 $\sigma'()$ 永远是正值，且永远不会接近于 0 。这可以避免普通 S 型神经元饱和时，学习速度减慢的现象。在书的后面部分，我们可以看到相关的例子。把四个等式 （BP1）- ( BP4 ) 记在脑中可以帮助我们理解为什么这类特定的修改会被尝试以及这类修改可能产生的影响。

这里写图片描述

问题：

修改反向传播函数的等式：我已经使用 Hadmard 乘积的方式展示了反向传播函数的等式（BP1 和 BP2）。这种展示形式可能让不熟悉 Hadmard 乘积符号的人感到不习惯。其实还有一种使用矩阵乘法表示的方法，一些读者可能会对此更加熟悉。
（1）尝试证明（BP1）可以被重写为下面的形式：

δ L = Σ' (z L) \nabla a C, (33)

$\begin{eqnarray} \delta^L = \Sigma'(z^L) \nabla_a C, \tag{33}\end{eqnarray}$

其中 $\Sigma'(z^L)$ 是一个 n*n 的矩阵，其对角线元素的值是 $\sigma'(z^L_j)$ ，他的非对角线元素是 0 。注意，这个矩阵通过矩阵乘法作用于 $\nabla_a C$

（2）尝试证明（BP2）可以被重写为
$δ l = Σ' (z l) (w l + 1) T δ l + 1 . (34)$ $\begin{eqnarray} \delta^l = \Sigma'(z^l) (w^{l+1})^T \delta^{l+1}. \tag{34}\end{eqnarray}$
(3) 把（1）和（2）的结果合并证明：

δ l = Σ' (z l) (w l + 1) T \dots Σ' (z L - 1) (w L) T Σ' (z L) \nabla a C (35)

$\begin{eqnarray} \delta^l = \Sigma'(z^l) (w^{l+1})^T \ldots \Sigma'(z^{L-1}) (w^L)^T \Sigma'(z^L) \nabla_a C \tag{35}\end{eqnarray}$

对于熟悉矩阵乘法的读者来说，这些等式可能比 (BP1) 和（BP2）更容易理解。而我专注于（BP1）和（BP2）的原因是，这种表示方法的数学实现起来更快。

四个基础等式的证明（选读）

我们现在来证明四个基础等式（BP1）- ( BP4 ). 这四个等式都是多变量微积分链式法则的结果。如果你熟悉链式法则的话，我强力建议你在阅读前尝试自行推导。

让我们从等式（BP1）开始，该等式给我们提供了一个关于输出误差的表达式 $\delta^L$ 。为了证明这个等式，回想一下定义：

δ L j = \partial C \partial z L j . (36)

$\begin{eqnarray} \delta^L_j = \frac{\partial C}{\partial z^L_j}. \tag{36}\end{eqnarray}$

应用链式法则，我们可以将上面的偏导数重新表达为与输出变量有关的形式。

δ L j = \sum k \partial C \partial a L k \partial a L k \partial z L j, (37)

$\begin{eqnarray} \delta^L_j = \sum_k \frac{\partial C}{\partial a^L_k} \frac{\partial a^L_k}{\partial z^L_j}, \tag{37}\end{eqnarray}$

其中，求和函数是针对输出层的所有神经元 k 进行的。显然，当 k = j 时，第 k 个神经元的输出激活量 $a^L_k$ 仅仅依赖于第 j（k）个神经元权重化输入 $z_j^L$ , 同理， $\partial a^L_k / \partial z^L_j$ 当 $k \neq j$ 时， $\partial a^L_k / \partial z^L_j$ 就为 0 。结果，我们就可以把之前的等式简化为：

δ L j = \partial C \partial a L j \partial a L j \partial z L j . (38)

$\begin{eqnarray} \delta^L_j = \frac{\partial C}{\partial a^L_j} \frac{\partial a^L_j}{\partial z^L_j}. \tag{38}\end{eqnarray}$

回想起 $a^L_j = \sigma(z^L_j)$ , 上面等式右端的第二项 $\frac{\partial a^L_j}{\partial z^L_j}$ 可以被重写为 $\sigma'(z^L_j)$ , 然后等式变成:

δ L j = \partial C \partial a L j σ' (z L j), (39)

$\begin{eqnarray} \delta^L_j = \frac{\partial C}{\partial a^L_j} \sigma'(z^L_j), \tag{39}\end{eqnarray}$

这恰恰就是（BP1）的成分表达形式。

下面我们将会证明（BP2），该等式为我们提供了前后两层的误差量 $\delta^{l}$ 和 $\delta^{l+1}$ 建立联系的等式。为了完成证明，我们想要把 $\delta^l_j = \partial C / \partial z^l_j$ 重写为有关 $\delta^{l+1}_k = \partial C / \partial z^{l+1}_k$ 的形式。我们可以通过链式法则来完成这一目标：

δ l j = = = \partial C \partial z l j \sum k \partial C \partial z l + 1 k \partial z l + 1 k \partial z l j \sum k \partial z l + 1 k \partial z l j δ l + 1 k, (40) (41) (42)

$\begin{eqnarray} \delta^l_j & = & \frac{\partial C}{\partial z^l_j} \tag{40}\\ & = & \sum_k \frac{\partial C}{\partial z^{l+1}_k} \frac{\partial z^{l+1}_k}{\partial z^l_j} \tag{41}\\ & = & \sum_k \frac{\partial z^{l+1}_k}{\partial z^l_j} \delta^{l+1}_k, \tag{42}\end{eqnarray}$

在最后一行，我们交换了（41）中两项的位置，然后根据 $\delta^{l+1}_k$ 的定义替换了对应的项。为了求出最后一行的第一项，我们注意到：

z l + 1 k = \sum j w l + 1 k j a l j + b l + 1 k = \sum j w l + 1 k j σ (z l j) + b l + 1 k . (43)

$\begin{eqnarray} z^{l+1}_k = \sum_j w^{l+1}_{kj} a^l_j +b^{l+1}_k = \sum_j w^{l+1}_{kj} \sigma(z^l_j) +b^{l+1}_k. \tag{43}\end{eqnarray}$

进行微分以后，我们得到：

\partial z l + 1 k \partial z l j = w l + 1 k j σ' (z l j) . (44)

$\begin{eqnarray} \frac{\partial z^{l+1}_k}{\partial z^l_j} = w^{l+1}_{kj} \sigma'(z^l_j). \tag{44}\end{eqnarray}$

这恰恰就是（BP2）的成分形式。

我们最后想要证明的等式是（BP3）和（BP4），这些也是使用链式法则证明的, 和前两个证明的方法类似。我把后面的证明留给读者作为一个小练习。

$$练习题
- 证明等式（BP3）和（BP 4）

至此就完成了反向传播的四个基本等式的证明。证明过程看上去好像比较复杂，但是它确实只是应用链式法则的结果。说的啰嗦一点，我们可以把反向传播看做是通过应用多变量微积分的链式法则来计算成本函数梯度的一种方式。这真的就是反向传播的全部了。其余的都是细节。

反向传播算法

反向传播算法给我们提供了一种计算成本函数梯度的方法，让我们把这个过程用算法形式描述出来：

输入 $x$ :设置输入层的激活量 $a^1$
前向反馈 : 针对每一层 $l=2,3,..., L$ 计算 $z^{l} = w^l a^{l-1}+b^l$ 和 $a^{l} = \sigma(z^{l})$ .
输出误差量 $\delta^L$ : 计算向量 $\delta^{L} = \nabla_a C \odot \sigma'(z^L)$
反向传播误差量： 对每一层 $l = L-1, L-2, \ldots, 2$ , 计算 $\delta^{l} = ((w^{l+1})^T \delta^{l+1}) \odot \sigma’(z^{l})$
输出：成本函数的梯度可以通过计算 $\frac{\partial C}{\partial w^l_{jk}} = a^{l-1}_k \delta^l_j$ 和 $\frac{\partial C}{\partial b^l_j} = \delta^l_j$ 得到。

审视这个算法，你会发现为什么它被称为“反向传播”，我们是从最后一层开始反向计算误差向量 $\delta ^l$ 的。我们从后向前的游历神经网络似乎非常奇怪。但是如果你思考一下反向传播的证明过程，反向的移动过程恰恰体现了成本是一个与神经网络输出相关的函数。为了理解成本是如何受到靠前的神经层的权重 w 和偏倚量 b 影响, 我们需要重复地应用链式法则，从后向前获得有用的表达式。

练习题

单个神经元被修改过后的反向传播：
- 假设我们在前向反馈网络中修改单一的一个神经元，使得该神经元的输出为 $f(\sum_j w_j x_j + b)$ , 其中 $f$ 是某个非 S 形函数。这种情况下，我们该如何修改反向传播算法呢？
线性神经元网络的反向传播：
- 假设我们把非线性的 $\sigma$ 函数替换为线性函数 $\sigma(z) = z$ , 请为这种情形重写反向传播算法。

正如我之前所描述的，反向传播算法计算针对单一的一个训练输入计算了成本函数的梯度， $C = C_x$ 。实践中，反向传播算法通常与学习算法（例如随机梯度下降）相结合，会需要为多个训练的输入计算梯度。具体而言，我们会对一个包含 m 训练输入的抽样迷你集计算梯度。下面的算法就是基于一个迷你集应用梯度下降算法的一个步骤：

输入一个训练抽样的集合
对每一个训练抽样 x : 设置对应的输入激活量 ax,1 , 并且进行下面的步骤：
- 前向反馈：针对每一层 $l=2,3,..., L$ 计算 $z^{x,l} = w^l a^{x,l-1}+b^l$ 和 $a^{x,l} = \sigma(z^{x,l})$ .
- 输出误差量 $\delta^{x,L}$ : 计算向量 $\delta^{x,L} = \nabla_a C \odot \sigma'(z^{x,L})$
- 反向传播误差量： 对每一层 $l = L-1, L-2, \ldots, 2$ , 计算 $\delta^{x,l} = ((w^{l+1})^T \delta^{x,l+1}) \odot \sigma’(z^{x,l})$
梯度下降：针对每一层 $l = L, L-1, \ldots, 2$ , 根据规则 $w^l \rightarrow w^l-\frac{\eta}{m} \sum_x \delta^{x,l} (a^{x,l-1})^T$ 和 $b^l \rightarrow b^l-\frac{\eta}{m} \sum_x \delta^{x,l}$

当然，为了实现梯度下降算法，你还需要在上面算法的外层嵌套一个对迷你集的遍历循环，然后在更外层套一个游历多训练世代（epoch）的循环。为了间接，这些循环被省略了。

反向传播算法的代码

在抽象地理解了反向传播算法后，我们现在可以理解上一章用于实现反向传播算法的代码了。回想上一章节包含在 Network 类中的 update_mini_batch 和 backprop 方法。这些代码是上面所描述的算法的一个直译实现。具体而言， update_mini_batch 方法通过计算当前 mini_batch 训练集抽样的梯度来更新 Network 的权重和偏倚量：

class Network(object):
...
    def update_mini_batch(self, mini_batch, eta):
        """Update the network's weights and biases by applying
        gradient descent using backpropagation to a single mini batch.
        The "mini_batch" is a list of tuples "(x, y)", and "eta"
        is the learning rate."""
        nabla_b = [np.zeros(b.shape) for b in self.biases]
        nabla_w = [np.zeros(w.shape) for w in self.weights]
        for x, y in mini_batch:
            delta_nabla_b, delta_nabla_w = self.backprop(x, y)
            nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)]
            nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)]
        self.weights = [w-(eta/len(mini_batch))*nw 
                        for w, nw in zip(self.weights, nabla_w)]
        self.biases = [b-(eta/len(mini_batch))*nb 
                       for b, nb in zip(self.biases, nabla_b)]

大部分的工作都被该行代码：delta_nabla_b, delta_nabla_w = self.backprop(x, y) 完成了，该行代码应用了 backprop 方法来算出偏导数 $\partial C_x / \partial b^l_j$ 和 $\partial C_x / \partial w^l_{jk}$ 。 `backprop` 方法几回完全遵循上一节的算法描述实现，除了一个小的改变- 我们用一种轻微不同的方法来对层数进行索引。这个改变意在利用 Python 语言的一个特性，也就是使用 list 为负值的索引来逆序访问一个 list , 也就是 `l[-3]` 是 list 导数第三个元素。 `backprop` 的代码如下，还有其他一些用于辅助计算 $\sigma$ 函数和其导数 $\sigma’$ ，以及成本函数导数的方法。有了这些内容，你应该能够理解下面的代码。如果有东西绊住了你，你可能可以通过翻阅上一章列出的原始完整版代码得到帮助。

class Network(object):
...
   def backprop(self, x, y):
        """Return a tuple "(nabla_b, nabla_w)" representing the
        gradient for the cost function C_x.  "nabla_b" and
        "nabla_w" are layer-by-layer lists of numpy arrays, similar
        to "self.biases" and "self.weights"."""
        nabla_b = [np.zeros(b.shape) for b in self.biases]
        nabla_w = [np.zeros(w.shape) for w in self.weights]
        # feedforward
        activation = x
        activations = [x] # list to store all the activations, layer by layer
        zs = [] # list to store all the z vectors, layer by layer
        for b, w in zip(self.biases, self.weights):
            z = np.dot(w, activation)+b
            zs.append(z)
            activation = sigmoid(z)
            activations.append(activation)
        # backward pass
        delta = self.cost_derivative(activations[-1], y) * \
            sigmoid_prime(zs[-1])
        nabla_b[-1] = delta
        nabla_w[-1] = np.dot(delta, activations[-2].transpose())
        # Note that the variable l in the loop below is used a little
        # differently to the notation in Chapter 2 of the book.  Here,
        # l = 1 means the last layer of neurons, l = 2 is the
        # second-last layer, and so on.  It's a renumbering of the
        # scheme in the book, used here to take advantage of the fact
        # that Python can use negative indices in lists.
        for l in xrange(2, self.num_layers):
            z = zs[-l]
            sp = sigmoid_prime(z)
            delta = np.dot(self.weights[-l+1].transpose(), delta) * sp
            nabla_b[-l] = delta
            nabla_w[-l] = np.dot(delta, activations[-l-1].transpose())
        return (nabla_b, nabla_w)

...

    def cost_derivative(self, output_activations, y):
        """Return the vector of partial derivatives \partial C_x /
        \partial a for the output activations."""
        return (output_activations-y) 

def sigmoid(z):
    """The sigmoid function."""
    return 1.0/(1.0+np.exp(-z))

def sigmoid_prime(z):
    """Derivative of the sigmoid function."""
    return sigmoid(z)*(1-sigmoid(z))

问题

完全基于矩阵进行的迷你集反向传播算法 。我们目前的随机梯度下降算法实现是在迷你集的训练抽样上进行循环完成的，但其实我们可以通过修改反向传播算法，使得一个迷你集的训练抽样的梯度可以被同时计算出来。方法是我们不再从一个单个输入向量 x 开始计算，而是从一个输入矩阵 $X = [x_1 x_2 \ldots x_m]$ 开始，其中的每一列就对应着迷你集中的每一个输入向量。我们通过乘以权重矩阵，然后加上一个对应的偏移量矩阵，然后在每一个项上应用 S 形函数。现在请你把这个方法的伪代码写出来。然后修改 network.py 使得它用这个完全基于矩阵的方法来进行计算。这种方法的好处是，它可以完全利用现代的线性代数代码实现库，加速对于迷你集的循环。（在我的笔记本电脑上，对于上一章我们所解决的 MNIST 的分类问题可以加速1/2）。实践中，所有正式的反向传播算法库都会使用这种完全基于矩阵的方法，或是该方法的变种形式。

在哪种意义上，反向传播算法是一个快速的算法？

在哪种意义上，反向传播算法是一个快速的算法？为了回答这个问题，让我考虑另外一种计算梯度的方法。想象现在是神经网络研究的早期，可能是19世纪50-60 年代，你是世界上第一个考虑用梯度下降方法来进行学习的人！但是为了实现这个想法，你需要计算成本函数的梯度。你回想了你关于微积分的只是，然后决定尝试看你是否能用链式法则来计算梯度。但是在做了一些尝试后，代数等式变得复杂起来，你有一些沮丧。于是你试图寻找另外一种方法。你决定把成本当做一个仅仅有关权重的方程 $C = C(w)$ （稍后我们会返回来查看偏倚量相关的情况）。你列出了权重 $w_1, w_2, \ldots$ ，然后试图针对某个特定的权重计算 $\partial C / \partial w_j$ 。一种显而易见的做法是来运用近似值：

\partial C \partial w j \approx C ( w + ϵ e j ) - C ( w ) ϵ, (46)

$\begin{eqnarray} \frac{\partial C}{\partial w_{j}} \approx \frac{C(w+\epsilon e_j)-C(w)}{\epsilon}, \tag{46}\end{eqnarray}$

其中， $\epsilon > 0$ 是一个很小的正值，而 $e_j$ 是第 $j$ 个方向上的单位向量。换句话说，我们可以通过为两个轻微不同的 $w_j$ 值来计算成本，进而应用等式（46）估算出 $\partial C / \partial w_j$ 。相同的思想可以被应用在偏倚量上。

这个方法看上去非常有前景。概念上足够简单，极度易于实现，仅仅几行代码就能实现。当然，这看上去比链式法则来计算梯度更有诱惑力！

不幸的是，这个方法虽然好像很有前景，但是当你用代码实现后会发现它极度缓慢。为了理解它为什么很慢，想象我们的神经网络中有一千万哥权重。那么针对每一个不同的权重 $w_j$ , 为了计算 $\partial C / \partial w_j$ 我们需要计算 $C(w+\epsilon e_j)$ 。那意味着为了计算梯度，我们需要计算一千万次成本函数，这需要一千万次的沿着网络的前向迭代计算（对每个训练输入而言）。此外，我们还需要计算 $C(w)$ ，这还会需要一次网络的前向迭代计算。这样总共会需要一千万零一次网络的遍历计算。

反向传播的聪明之处在于，它可以使我们仅仅用一次网络的前向迭代计算和紧随其后的一次反向迭代计算，就同时计算所有的偏导数 $\partial C / \partial w_j$ 。粗略地来说，反向迭代的计算开销大约是一次正向迭代计算的两倍。把这个计算量和一万零一次的前向迭代计算对比一下！所以，即便反向起算看上去比公式 (46) 的方法复杂了许多，但它依旧非常，非常快。

这个加速方法是1986年第一次被完全接受，之后极大地扩展了神经网络可以解决的问题范围。这样，又反过来促进一大批人使用神经网络。当然，反向传播不是一个灵丹妙药。甚至在19世纪80年代，人们就遭遇了该方法的瓶颈，尤其是当人们视图用这个方法训练深度神经网络（有很多隐藏层的神经网络）时。在这本书的后面，我们会看到现代计算机和一些聪明的想法是如何使得用反向传播训练深度神经网络成为可能的。

反向传播：整体图景

正如我之前解释过的，反向传播算法有两个神秘之处。

第一，这个算法到底做了什么。我们已经了解了误差量从输出被反向传播的过程。但是，我们能进一步深入，对我们所做的这一系列矩阵和向量乘法构建出更多的直觉性认识吗？

第二，一个人如何才能在没有先行者参考的情况下，发现这个算法。理解算法的步骤，或甚至理解算法的证明过程是一回事，理解一个问题，然后作为第一个人独立发现解决这个问题的算法又是另一回事。有没有一条可行的推理线索可以指引你发现反向传播算法？

在这一小节，我会解答这两个谜题

为了改善我们对反向传播算法工作内容的直觉性理解，让我们想象我们对神经网络中的某个权重 $w^l_{jk}$ 做了一个小的改动：
这里写图片描述

这会导致对应的神经元的激活量发生改变：

这里写图片描述

然后这会进一步会导致下一层所有的神经元激活量都发生变化：

这里写图片描述

这些改变会进一步导致下一层的变化，依次类推直到影响最后一层的输出，然后影响到成本函数值的变化。

这里写图片描述

成本函数值的改变量 $\Delta C$ 和权重值的改变量 $\Delta w^l_{jk}$ 的关系可以用如下等式描述：

Δ C \approx \partial C \partial w l j k Δ w l j k . (47)

$\begin{eqnarray} \Delta C \approx \frac{\partial C}{\partial w^l_{jk}} \Delta w^l_{jk}. \tag{47}\end{eqnarray}$

这给我们提供了一个思路，可以通过仔细地观察 $w^l_{jk}$ 的微小变化是如何扩散导致成本值 $C$ 的微小变化，来计算 $\frac{\partial C}{\partial w^l_{jk}}$ 。如果我们可以将这一路的变化用一些易于计算的量表达出来，那么我们就应该能计算出 $\partial C / \partial w^l_{jk}$

让我们来试着实现它。改变量 $\Delta w^l_{jk}$ 导致第 $l$ 层的第 $j$ 个神经元的激活量产生了微小的变化 $\Delta a^{l}_j$ 。这个变化可以通过此公式计算：

Δ a l j \approx \partial a l j \partial w l j k Δ w l j k . (48)

$\begin{eqnarray} \Delta a^l_j \approx \frac{\partial a^l_j}{\partial w^l_{jk}} \Delta w^l_{jk}. \tag{48}\end{eqnarray}$

激活量的改变 $\Delta a^l_{j}$ 会导致下一层（第 $l+1$ 层）上所有神经元的激活量都改变。我们先专注于其中一个受到影响的激活量 $a^{l+1}_q$ 来进行分析。

这里写图片描述

事实上，它会导致如下的变化：

Δ a l + 1 q \approx \partial a l + 1 q \partial a l j Δ a l j . (49)

$\begin{eqnarray} \Delta a^{l+1}_q \approx \frac{\partial a^{l+1}_q}{\partial a^l_j} \Delta a^l_j. \tag{49}\end{eqnarray}$

用等式（48）进行代入得到

Δ a l + 1 q \approx \partial a l + 1 q \partial a l j \partial a l j \partial w l j k Δ w l j k . (50)

$\begin{eqnarray} \Delta a^{l+1}_q \approx \frac{\partial a^{l+1}_q}{\partial a^l_j} \frac{\partial a^l_j}{\partial w^l_{jk}} \Delta w^l_{jk}. \tag{50}\end{eqnarray}$

当然，改变量 $\Delta a^{l+1}_q$ 会进一步导致下一层神经元中激活量的变化。事实上，我们可以想象出来一条从 $w^l_{jk}$ 一直到成本值 $C$ 的路径，每一个激活量的改变会导致下一层激活量的改变，直到对最终的成本值产生影响，如果激活量序列是 $a^l_j, a^{l+1}_q, \ldots, a^{L-1}_n, a^L_m$ ，那么对应的成本改变量表达式就是：

Δ C \approx \partial C \partial a L m \partial a L m \partial a L - 1 n \partial a L - 1 n \partial a L - 2 p \dots \partial a l + 1 q \partial a l j \partial a l j \partial w l j k Δ w l j k, (51)

$\begin{eqnarray} \Delta C \approx \frac{\partial C}{\partial a^L_m} \frac{\partial a^L_m}{\partial a^{L-1}_n} \frac{\partial a^{L-1}_n}{\partial a^{L-2}_p} \ldots \frac{\partial a^{l+1}_q}{\partial a^l_j} \frac{\partial a^l_j}{\partial w^l_{jk}} \Delta w^l_{jk}, \tag{51}\end{eqnarray}$

其中，我们为每一个经过的神经元都选用了 $\partial a / \partial a$ 形式的项进行了表达，在最后用 $\partial C/\partial a^L_m$ 进行了表达。这个表示了神经网络上某一条路径上的改变量对成本值 $C$ 的影响。当然， $w^l_{jk}$ 的改变所产生影响的路径并不止这一条，我们现在仅仅考虑了一条路径。为了计算成本 $C$ 的总变化量，我们需要把所有成本到最终成本值之间可能产生的影响路径都汇总起来，即：

$\begin{eqnarray} \Delta C \approx \sum_{mnp\ldots q} \frac{\partial C}{\partial a^L_m} \frac{\partial a^L_m}{\partial a^{L-1}_n} \frac{\partial a^{L-1}_n}{\partial a^{L-2}_p} \ldots \frac{\partial a^{l+1}_q}{\partial a^l_j} \frac{\partial a^l_j}{\partial w^l_{jk}} \Delta w^l_{jk}, \tag{52}\end{eqnarray}$
其中，我们加总了所有所有可能的神经元序列组合。和公式（47）进行对比，我们可以得到：

\partial C \partial w l j k = \sum m n p \dots q \partial C \partial a L m \partial a L m \partial a L - 1 n \partial a L - 1 n \partial a L - 2 p \dots \partial a l + 1 q \partial a l j \partial a l j \partial w l j k . (53)

$\begin{eqnarray} \frac{\partial C}{\partial w^l_{jk}} = \sum_{mnp\ldots q} \frac{\partial C}{\partial a^L_m} \frac{\partial a^L_m}{\partial a^{L-1}_n} \frac{\partial a^{L-1}_n}{\partial a^{L-2}_p} \ldots \frac{\partial a^{l+1}_q}{\partial a^l_j} \frac{\partial a^l_j}{\partial w^l_{jk}}. \tag{53}\end{eqnarray}$

现在等式（53）看起来比较复杂了。然而，它却有一个很好的直觉性解释。我们在计算成本 C 相对于神经网络中的一个权重变化率，而这个等式告诉我们，神经网络中的两个神经元之间的每一条边（权重）都和一个因子存在某种联系，这个因子就是其中一个神经元的激活量相对于另外一个激活量的偏导数。而连接两个神经元的路径上的第一条边的因子比较特殊，是 $\partial a^{l}_j / \partial w^l_{jk}$ , 之后的边的因子是 $\frac{\partial a^{l+1}_q}{\partial a^{l}_j}$ , 如果我们将这条路径上每条边的依次相乘作为这条路径的因子，那么，成本值相对于权重 $w^l_{jk}$ 的总体改变率 $\partial C / \partial w^l_{jk}$ 就恰好是该权重所在边到最终成本值的所有路径的因子。通过图例展示，就是如下的效果：

这里写图片描述

刚才所展示的只是一个启发性质的论证，一种用于思考对权重进行微调后会发生什么的方法。现在让我们勾勒出一条线索，使你可以进一步深化这个论证。

首先，你可以推到中等式（53）中每一个偏导数的表达式，这用于一点微分学知识就能做到。完成了之后，你可以尝试这思考如何把这个包含众多下标的求和公式写成矩阵相乘的形式。这件事真的做起来会乏味，还需要一些毅力，但不需要超凡的洞察力。在完成了所有这些后，试着对其进行尽可能的简化，你会发现你最终就得到了反向传播算法。然后你就可以把反向传播算法当做一个为所有路径求因子和的方式。或者，换种说法，反向传播算法是一种追踪权重（偏倚量）的变动如何一步步扩散至输出，最后影响成本的方法。

现在，我并不打算一步步展示这个过程。它非常散乱且需要极度的细心去完成好每个细节。如果你有兴趣挑战一下，你可能会享受这个尝试的过程。如果你不感兴趣，那么我希望这个思考过程可以为你提供一些反向传播算法工作原理的深入认识。

现在讨论另一个谜题，反向传播算法是如何被第一个人发现的呢？事实上，如果你沿着我刚才所描述的方法进行尝试，就会发现反向传播算法的证明方法。不幸的是，这个证明非常长，且比我本章之前的描述要冗长许多。那么，问题就来了，短的那个证明是如何被发现的。事实上，当你写下来长的证明方式的所有细节后，你会发现其中有好几处非常明显的可以简化的地方。你进行这些简化，会得到一个更短的证明。然后把它写下来，你会进一步发现可以简化的地方，你再次重复。在经过几次重复操作后，你就会得到我们先前看到的，简短的，但是有一些晦涩的证明，晦涩的原因是简化的过程相当于去除了你一路推导的路标。我想请你相信我，要推导出之前的证明，真的不存在什么神秘之处，它就是对我之前所勾勒的证明过程做了很多简化工作而已。