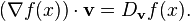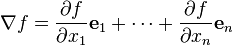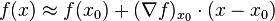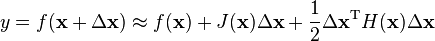梯度（Gradient）：
wiki上的定义：
The gradient of f is defined as the unique vector field whose dot product with any vector v at each point x is the directional derivative of f along v. That is,
f 的梯度，是与在每一点x的任意向量v的点积为f沿着v的方向的导数的唯一的向量场。
说的真复杂，但是关键信息是，对于一个固定的x而言，梯度是一个向量。
直角坐标系中，梯度是这样一个向量：
其分量由f在各个基的方向上的偏导组成
笛卡尔坐标系中，就是：
沿着i方向的导数，就是i轴方向的分量
和一阶泰勒公式类似：
梯度和df之间关系：
http://en.wikipedia.org/wiki/Gradient#Differential_or_.28exterior.29_derivative
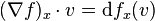
记df是差分函数 x->dfx
把x看做变量，
R看做列向量空间，df可以看做一个行向量，
于是dfx就是一个矩阵相乘(df*列向量空间的基)的形式。梯度就是对应的列向量
由于v是任意的，所以函数相等，其元素也相等。
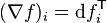
Jacobian:
对于值为标量的多变量的函数 f(x)，我们使用梯度，但是如果是值为向量的多变量的函数怎么办呢
雅克比矩阵实际上是对于梯度的一种泛化，
记m为函数值的维度，记n为变量维度
m = 1时，函数的雅克比矩阵就是梯度
m = 1而且n=1时，函数的雅克比矩阵和梯度就是简单的导数。
这里wiki给出了一个小例子，在图像变换（变量是位置x和y）中，已知某一位置的变换情况，就可以利用雅克比矩阵来估计周围情况，这和用一阶导近似某一点周围的函数值是一样的。
The Jacobian can also be thought of as describing the amount of "stretching", "rotating" or "transforming" that a transformation imposes locally. For example, if 
is used to transform an image, the Jacobian of 
, 
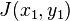describes how the image in the neighborhood of 
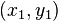is transformed.
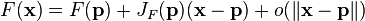
http://en.wikipedia.org/wiki/Jacobian_matrix#Dynamical_systems
a stationary point is related to the eigenvalues of JF(x0)
某种意义上说，梯度和雅克比矩阵都是一种一阶导数（二者针对的函数的值不同）
二阶导数是什么呢？
一个值为标量的多变量函数的梯度的雅克比矩阵就是二阶导数，也就是Hessian矩阵
= 
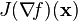.![H(f) = \begin{bmatrix}\dfrac{\partial^2 f}{\partial x_1^2} & \dfrac{\partial^2 f}{\partial x_1\,\partial x_2} & \cdots & \dfrac{\partial^2 f}{\partial x_1\,\partial x_n} \\[2.2ex]\dfrac{\partial^2 f}{\partial x_2\,\partial x_1} & \dfrac{\partial^2 f}{\partial x_2^2} & \cdots & \dfrac{\partial^2 f}{\partial x_2\,\partial x_n} \\[2.2ex]\vdots & \vdots & \ddots & \vdots \\[2.2ex]\dfrac{\partial^2 f}{\partial x_n\,\partial x_1} & \dfrac{\partial^2 f}{\partial x_n\,\partial x_2} & \cdots & \dfrac{\partial^2 f}{\partial x_n^2}\end{bmatrix}.](https://upload.wikimedia.org/math/f/7/2/f7296865484b39fcbac598a99b7f3dbb.png)
类似泰勒二阶公式：
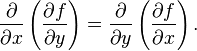
于是Hessian是对称矩阵。