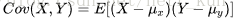一、数据降维技术
主要有三种：PCA（主成分分析法）、FA（因子分析法）、ICA（独立成分分析法），应用最广范、最广为人知的就是PCA方法，这里主要分析PCA方法。
二、PCA
首先要知道的是PCA降维的原理和目的是什么？
原理：
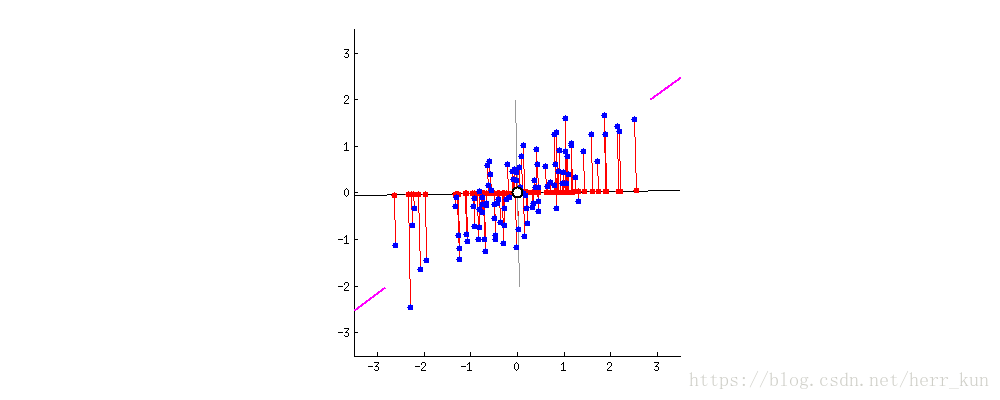
最大化投影后数据的方差，表示为在某一维度的投影方差最大，如下图中当前位置不是投影方差最大的位置，因为好多点重合到了一起，因此在该维度我们就很难区分重叠的数据，当途中的直线旋转到断线的位置时，此时可以看到大部分的点是很分散的，对应着方差很大。此时就将二维的数据（x-y平面），投影到了一维上（一条直线上）。
PCA的实现用到了协方差矩阵，那么你可能会问什么是协方差矩阵，为什么要用协方差矩阵？
首先回答第一个问题，什么是协方差矩阵。首先大家肯定知道什么是方差，方差就是描述一维数据的分布离散程度，有了这个概念我们就可以相应的拓展到多维数据了，协方差顾名思义就是不是真正的方差，其主要是为了表示两个变量之间的相关关系（相关系数也是表示两个变量之间的相关关系，那么两者之间的区别在哪里呢，后续后提到），而协方差矩阵是应用到更多维数据上的，那么在多维数据里面又表示什么意思呢？
假设样本数据有r维（组成一个r维向量），共有n个样本。组成r*n矩阵A，矩阵每一列是一个样本，行是各个不同的特征维度。求解协方差矩阵S=AAT（最好先将A进行每个维度上的数据进行中心化A→C再求协方差矩阵S=CCT
），
S是r*r的方阵，用X(j)表示样本数据的第j维数据，则求解协方差为：（图来自babywong的博客）
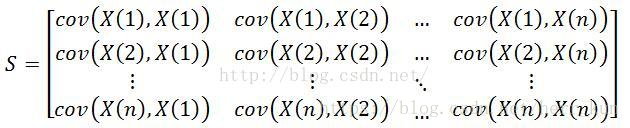
我们可以看到S矩阵的对角线上就是对应的特征的方差，其余非对角线上就是我们前面提到协方差的定义，也就是两个特征之间的相关关系。再回顾一下我们用PCA的目的，为了减少维度，但是不损失信息。那现在对应上图中的矩阵，我们希望做的就是取前N个方差（对应着能量）比较大的特征（对应着K个维度里面取N维），能够表示大部分的数据信息；我们还想使得各个特征之间的协方差（相关关系）最小，以便于我们区分开来。
所以经过上述的解释就比较明白了协方差矩阵到底隐藏了什么秘密，要我们取分解它。想要实现上述的目的需要将协方差矩阵进行特征值分解（eig），得到特征值和特征向量，然后将特征值进行从大到小的排序，保留最上面的N个特征向量，最后再与C矩阵相乘就得到我们降维以后的矩阵了。
PS：（查看矩阵降维后所保留的信息比例-可以通过计算前N个特征值的和除以所有特征值的和来实现）
三、SVD及异同分析
大家肯定都知道大名鼎鼎的SVD（奇异值分解），矩阵经过SVD分解后生成三个矩阵，这块就不细说了，下面主要来分析两者之间的异同点（严格的说是SVD和特征值分解之间的异同）：
同：1、SVD中的对焦矩阵中的值（奇异值）就是协方差矩阵特征分解的特征值的平方根（因此SVD运算速度更快），2、可以找到一个标准正交矩阵，将特征值分解写成SVD的形式，类似
P
-1
P(AA
T
)PTP= P
-1
ΛP 即S=AA
T
= P
-1
ΛP， ：
异：1、SVD不用计算协方差这一步，直接对矩阵C进行奇异值分解，而PCA需要通过计算协方差矩阵，然后在进行特征值分解。2、特征值分解只能对方阵进行分解，而SVD都可以。
四、协方差和相关关系
注意，这里的两者都指的是两个变量之间（也可认为两维（受矩阵影响太深）），比如两个变量X，Y，如果两者之间的
协方差为正，则说明两者之间为正相关，为负，则说明负相关。
相关系数的原理概念和协方差一摸一样，只不过不同的是相关系数的计算公式为：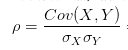
很明显在原有的协方差上面除以了两者标准差的乘积，只是为了进行标准化，消除X Y之间的量纲的影响。