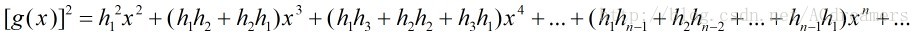Catalan数一瞥:
关于Catalan,这是一个特殊的数列,可以方便求解许多问题。
这里,先给出Catalan数的通项公式,再举例进行进一步的分析:。
先分析它的递推关系:
题目:在一个有n+2条边的多边形中,我们可以画出n-1条不相交的对角线将多边形分为n个三角形,设所有满足条件的方案数是,定义
=1,求
、
。
分析:由题意,我们知道,有n+2条边的多边形,就相当于有n+2个点。我们又知道,因为每个点都通向两外两个相邻的点,那么,与它不相交的点就有n个点。给你们画张图就知道了。此时,n=4。(如下图)。

那我们来帮助理解一下,什么叫做n-1条不相交对角线。
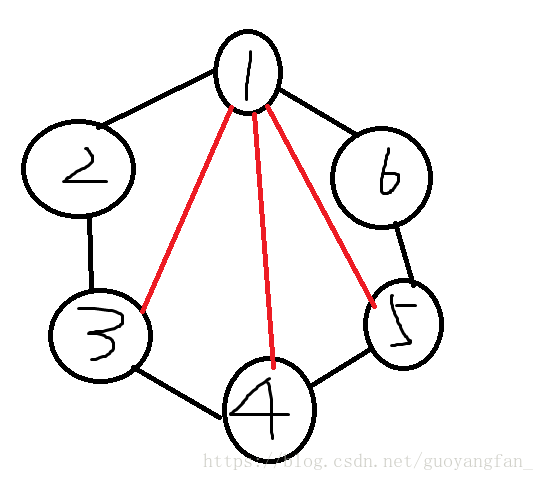

那么,我们可以得到,每次在我们连接完一条不相交的对角线后,我们会发现,这条对角线把当前图行分割成了2部分。那我们设其中一块有k+2条边(这样我们就可以得到k个三角形)。同理,另一块图形我们会得到n-1-k个三角形。因为乘法原理,这样剖分的方案数就为(其中n为三角形的总数量,看前面n的介绍)。
显然,k可以从0一直变化到n-1(注意,考虑边界情况,并注意到这里的对角线不相交,所以这里不会出现重复计数)。
所以,递推式为。
这个数列就是著名的Catalan数列。
现在,我们将这玩意整成我们熟悉的带有组合数的通项公式:
这里用到了生成函数:我们很容易写出的生成函数
我们进一步计算
因为有:

所以有: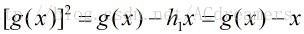
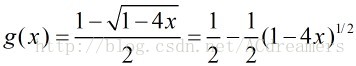
那么根据牛顿二项式有:
那么带入化简得到:
那么我们最终得到:
所以:,这就是Catalan的推导过程。
再来用第二种方式看一看Catalan数:
题目:我们有n个+1和n个-1,将它们排列起来,其中任何长度的前缀和都大于等于0。问,有几种排列方案?、
这时,答案。
解释:我们设表示满足条件的排列数的个数。再设
表示不满足条件即任何长度的前缀和有一个或多个前缀和答案小于0。那么由组合数定义我们可以知道:
+
=
。
接下来,我们试图求出。
根据题目定义,我们先设k满足某些前缀和小于0,且这个k必须要保证最小。
那么我们可以知道,前k个数中-1的数量肯定比+1的数量多1。
那么,我们根据k的定义可以知道,k是一个奇数(因为前缀和小于0了,+1与-1的数量不匹配),且前k-1个数中+1和-1的数量刚好相等(第k个数必须是-1,这样才能保证k最小)
那么,我们将前k个数取反(每一个数1变0或者0变1),就可以得到有n+1个+1和n-1个-1(因为前k个数中-1的数量比+1的数量多1)。但这个操作是可逆的。我们设k满足某些前缀和大于0,且这个k必须要保证最小。得出这个k后将前k个数取反,就可以得到原数列。
所以,不可接受的数列 就和 有n+1个+1和n-1个-1的数列是一一对应的。
所以,不可接受的数列。
所以,+
=
。
所以,=
=
。