决策树详解

原文链接：https://blog.csdn.net/zhaocj/article/details/50503450#commentBox

建议阅读此文章的同志们最好拿支笔，拿张纸，把函数抄下来，运算过程跟着算一遍比较好。

一、原理

决策树是一种非参数的监督学习方法，它主要用于分类和回归。决策树的目的是构造一种模型，使之能够从样本数据的特征属性中，通过学习简单的决策规则——IF THEN规则，从而预测目标变量的值。

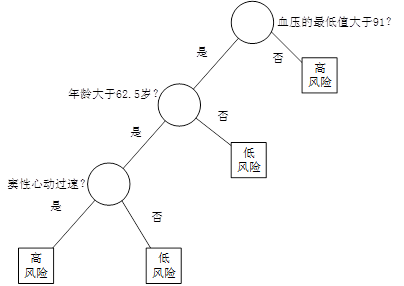
图1 决策树

例如，在某医院内，对因心脏病发作而入院治疗的患者，在住院的前24小时内，观测记录下来他们的19个特征属性——血压、年龄、以及其他17项可以综合判断病人状况的重要指标，用图1所示的决策树判断病人是否属于高危患者。在图1中，圆形为中间节点，也就是树的分支，它代表IF THEN规则的条件；方形为终端节点（叶节点），也就是树的叶，它代表IF THEN规则的结果。我们也把第一个节点称为根节点。

决策树往往采用的是自上而下的设计方法，每迭代循环一次，就会选择一个特征属性进行分叉，直到不能再分叉为止。因此在构建决策树的过程中，选择最佳（既能够快速分类，又能使决策树的深度小）的分叉特征属性是关键所在。这种“最佳性”可以用非纯度（impurity）进行衡量。如果一个数据集合中只有一种分类结果，则该集合最纯，即一致性好；反之有许多分类，则不纯，即一致性不好。有许多指标可以定量的度量这种非纯度，最常用的有熵，基尼指数（Gini Index）和分类误差，它们的公式分别为：

（1）

（2）

（3）

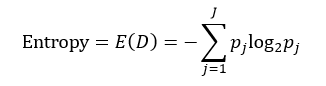
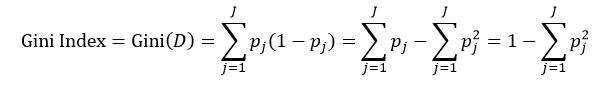
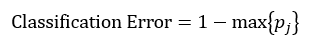
上述所有公式中，值越大，表示越不纯，这三个度量之间并不存在显著的差别。式中D表示样本数据的分类集合，并且该集合共有J种分类，pj表示第j种分类的样本率：

（4）

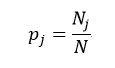
式中N和Nj分别表示集合D中样本数据的总数和第j个分类的样本数量。把式4带入式2中，得到：

（5）

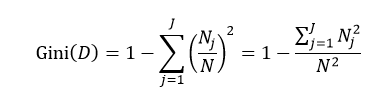
目前常用的决策树的算法包括ID3（Iterative Dichotomiser 3，第3代迭戈二叉树）、C4.5和CART（ClassificationAnd Regression Tree，分类和回归树）。前两种算法主要应用的是基于熵的方法，而第三种应用的是基尼指数的方法。下面我们就逐一介绍这些方法。

ID3是由Ross Quinlan首先提出，它是基于所谓“Occam'srazor”（奥卡姆剃刀），即越简单越好，也就是越是小型的决策树越优于大型的决策树。如前所述，我们已经有了熵作为衡量样本集合纯度的标准，熵越大，越不纯，因此我们希望在分类以后能够降低熵的大小，使之变纯一些。这种分类后熵变小的判定标准可以用信息增益（Information Gain）来衡量，它的定义为：

（6）

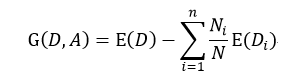
该式表示在样本集合D下特征属性A的信息增益，n表示针对特征属性A，样本集合被划分为n个不同部分，即A中包含着n个不同的值，Ni表示第i个部分的样本数量，E(Di)表示特征属性A下第i个部分的分类集合的熵。信息增益越大，分类后熵下降得越快，则分类效果越好。因此我们在D内遍历所有属性，选择信息增益最大的那个特征属性进行分类。在下次迭代循环中，我们只需对上次分类剩下的样本集合计算信息增益，如此循环，直至不能再分类为止。

C4.5算法也是由Quinlan提出，它是ID3算法的扩展。ID3应用的是信息增益的方法，但这种方法存在一个问题，那就是它会更愿意选择那些包括很多种类的特征属性，即哪个A中的n多，那么这个A的信息增益就可能更大。为此，C4.5使用信息增益率这一准则来衡量非纯度，即：

（7）

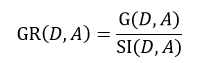
式中，SI(D, A)表示分裂信息值，它的定义为：

（8）

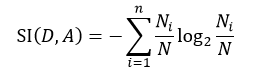
该式中的符号含义与式6相同。同样的，我们选择信息增益率最大的那个特征属性作为分类属性。

CART算法是由Breiman等人首先提出，它包括分类树和回归树两种。我们先来讨论分类树，针对特征属性A，分类后的基尼指数为：

（9）

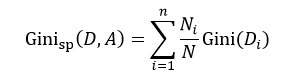
该式中的符号含义与式6相同。与ID3和C4.5不同，我们选择分类基尼指数最小的那个特征属性作为分类属性。当我们每次只想把样本集合分为两类时，即每个中间节点只产生两个分支，但如果特征属性A中有多于2个的值，即n> 2，这时我们就需要一个阈值β，它把D分割成了D1和D2两个部分，不同的β得到不同的D1和D2，我们重新设D1的样本数为L，D2的样本数为R，因此有L+R = N，则式9可简写为：

（10）

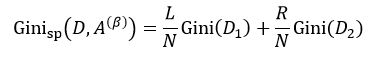
我们把式5带入上式中，得到：

（11）

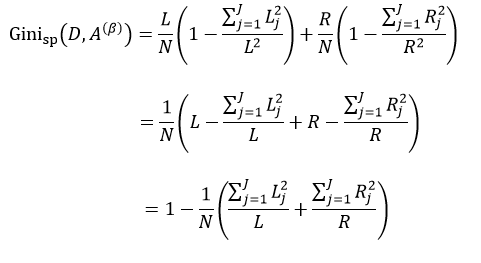
式中，∑Lj = L，∑Rj = R。式11只是通过不同特征属性A的不同阈值β来得到样本集D的不纯度，由于D内的样本数量N是一定的，因此对式11求最小值问题就转换为求式12的最大值问题：

（12）

以上给出的是分类树的计算方法，下面介绍回归树。两者的不同之处是，分类树的样本输出（即响应值）是类的形式，如判断蘑菇是有毒还是无毒，周末去看电影还是不去。而回归树的样本输出是数值的形式，比如给某人发放房屋贷款的数额就是具体的数值，可以是0到120万元之间的任意值。为了得到回归树，我们就需要把适合分类的非纯度度量用适合回归的非纯度度量取代。因此我们将熵计算用均方误差替代：

（13）

式中N表示D集合的样本数量，yi和ri分别为第i个样本的输出值和预测值。如果我们把样本的预测值用样本输出值的平均来替代，则式13改写为：

（14）

上式表示了集合D的最小均方误差。

（我觉14得此处的运算貌似有点小问题，第二步到第三步中间项的计算，把累加号提进去之后）

如果针对于某种特征属性A，我们把集合D划分为s个部分，则划分后的均方误差为：

（15）

式中Ni表示被划分的第i个集合Di的样本数量。式15与式14的差值为划分为s个部分后的误差减小：

（16）

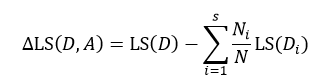
与式6所表示的信息增益相似，我们寻求的是最大化的误差减小，此时就得到了最佳的s个部分的划分。

同样的，当我们仅考虑二叉树的情况时，即每个中间节点只有两个分支，此时s= 2，基于特征属性A的值，集合D被阈值β划分为D1和D2两个集合，每个集合的样本数分别为L和R，则：

（17）

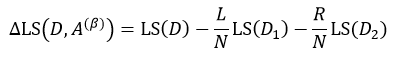
把式14带入上式，得：

（18）

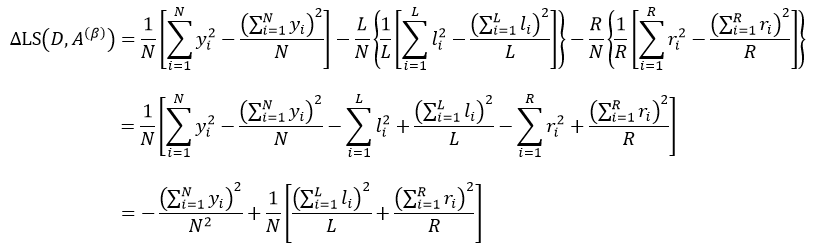
式中，yi是属于集合D的样本响应值，li和ri分别是属于集合D1和D2的样本响应值。对于某个节点来说，它的样本数量以及样本响应值的和是一个定值，因此式18的结果完全取决于方括号内的部分，即：

（19）

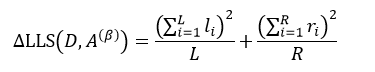
因此求式18的最大值问题就转变为求式19的最大值问题。