一、相机模型、内参、外参，畸变以及相机标定

1、坐标系转换

（1）坐标系概念

世界坐标系：与相机无关，独立的坐标系

世界坐标系（world coordinate）(Xw,Yw,Zw)也称为测量坐标系，是一个三维直角坐标系，以其为基准可以描述相机和待测物体的空间位置。世界坐标系的位置可以根据实际情况自由确定。

相机坐标系：与相机有关的坐标系，其中X,Y与成像平面平行，原点为光心，Z为光轴方向

相机坐标系（camera coordinate）(Xc,Yc,Zc)也是一个三维直角坐标系，原点位于镜头光心处，x、y轴分别与相面的两边平行，z轴为镜头光轴，与像平面垂直。

图像坐标系：平面二维坐标系，与成像平面平行，原点在图像中心。

像素坐标系：以像素为单位，原点在图像左上角。

（2）坐标系之间的转换

世界坐标系与相机坐标系：

反映相机在世界坐标系中的位置，也可以叫做外参，用一个旋转R和平移T矩阵表示。其转换关系如下所示：

其中R为3*3的旋转矩阵，t为3*1的平移矢量，(xc,yc,zc,1)T为相机坐标系的齐次坐标，(xw,yw,zw,1)T为世界坐标系的齐次坐标。

推导过程：

设Pc是空间点P在相机坐标系坐标，Pw是其在世界坐标系下的坐标，则Pc和Pw之间的坐标变换可以用一个旋转矩阵R和一个平移向量t表示，如下所示

$Pc=PwR+t$ ，坐标矩阵表示如下所示,R为3*3的旋转矩阵，t为3*1的平移矩阵，分别表示在x,y,z三个方向上的旋转平移

$\begin{bmatrix} Xc\\ Yc\\ Zc \end{bmatrix}=\begin{bmatrix} R11 & R12 & R13\\ R21& R22& R23\\ R31& R32& R33 \end{bmatrix} \begin{bmatrix} Xw\\ Yw\\ Zw \end{bmatrix}+\begin{bmatrix} t1\\ t2\\ t3 \end{bmatrix}$

为了计算方便，改为齐次坐标表示如下所示

$\begin{bmatrix} Xc\\ Yc\\ Zc\\ 1 \end{bmatrix}=\begin{bmatrix} Xw\\ Yw\\ Zw\\ 1 \end{bmatrix} \begin{bmatrix} R11 & R12& R13 & t1\\ R 21& R22& R23 &t2 \\ R31& R32& R33& t3\\ 0& 0& 0 & 1 \end{bmatrix}=\begin{bmatrix} R &t \\ 0^{T}& 1 \end{bmatrix} \begin{bmatrix} Xw\\ Yw\\ Zw\\ 1 \end{bmatrix}$

三维相机坐标系与二维图像坐标系的转换：利用小孔成像原理。

相机针孔成像模型如下所示：

相机坐标系与图像坐标系转换为空间点P（Xc,Yc,Zc）和其像点P（x,y）的转换，假设空间在P在相机坐标系中的坐标为 $[Xc,Yc,Zc]^{T}$ ,其成像点p在成像平面上的坐标为 $[x,y]^{T}$ ，那么两者可以用如下公式表示

$s\begin{bmatrix} x\\ y\\ 1 \end{bmatrix}=\begin{bmatrix} f &0 &0 &0\\ 0 & f &0&0 \\ 0&0 &1&0 \end{bmatrix} \begin{bmatrix} Xc\\ Yc\\ Zc\\ 1 \end{bmatrix}$ ，其中f为相机焦距（光心到图像平面的距离），s为比例因子（s不为0），公式中为齐次坐标表示。

推导过程如下：

P在相机坐标系中的坐标为 $[Xc,Yc,Zc]^{T}$ ,其成像点p在成像平面上的坐标为 $[x,y]^{T}$ ，像点p在相机坐标系上的坐标为 $[x',y',z']^{T}$ ,其中z'=f，x‘=x，y'=y。

根据小孔成像原理，有如下相似三角形：

根据三角形的相似关系（图中），有如下公式：

$\frac{Zc}{f}=\frac{Xc}{x'}=\frac{Yc}{y'}$ ,公式整理可以得到 $\left\{\begin{matrix} x'=f\frac{Xc}{Zc}\\ y'=f\frac{Yc}{Zc} \\ z'=f \end{matrix}\right.$ ，即有 $\left\{\begin{matrix} x=f\frac{Xc}{Zc}\\ y=f\frac{Yc}{Zc}\end{matrix}\right.$ ，扩展坐标的维度）将其线性化，则有如下表达式

$\begin{bmatrix} \breve{x}\\ \breve{y}\\ \breve{z} \end{bmatrix}=\begin{bmatrix} f & 0& 0& 0\\ 0& f & 0& 0\\ 0& 0& 1& 0\\ \end{bmatrix} \begin{bmatrix} Xc\\ Yc\\ Zc\\ 1 \end{bmatrix}=\begin{bmatrix} fXc\\ fYc\\ Zc \end{bmatrix}=\begin{bmatrix} xZc\\ yZc\\ Zc \end{bmatrix}$ ,其中 $\left\{\begin{matrix} x=\breve{x}/Zc\\ y=\breve{y}/Zc\\ Zc\neq 0 \end{matrix}\right.$ ,则从相机坐标到平面坐标的转换关系如下：

$Zc\begin{bmatrix} x\\ y\\ 1 \end{bmatrix}=\begin{bmatrix} f &0 &0 &0\\ 0 & f &0&0 \\ 0&0 &1&0 \end{bmatrix} \begin{bmatrix} Xc\\ Yc\\ Zc\\ 1 \end{bmatrix}$ .

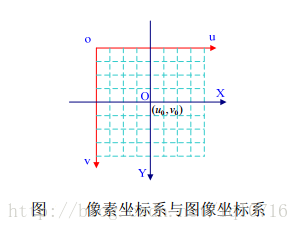
图像坐标系与像素坐标系 $\Rightarrow$ 像素坐标系到相机坐标系

æ¤å¤è¾å¥å¾ççæè¿°

二维像素坐标系和二维图像坐标系之间有一个平移和缩放变换。推导过程如下

设点p图像坐标为p(x,y)，像素坐标为(u,v)，像素坐标原点在左上角，u轴水平向左，v轴竖直向下，图像坐标原点在图像中心点，其之间有一个平移(cx,cy)，像素是个矩形块，设其在x,y方向上长度分别为 $\alpha ,\beta$ ,那么从图像坐标系变为像素坐标系为x方向缩放 $\alpha$ 倍，竖直方向缩放 $\beta$ 倍，且平移(cx，cy),有如下公式

$\left\{\begin{matrix} u=\alpha x+c_{x}\\ v=\beta y+c_{y} \end{matrix}\right.= \left\{\begin{matrix} u=\alpha f\frac{Xc}{Zc}+c_{x}\\ v=\beta f\frac{Yc}{Zc}+c_{y} \end{matrix}\right.$ ,则有

$\begin{bmatrix} u\\ v\\ 1 \end{bmatrix}=\frac{1}{Zc}\begin{bmatrix} f_{x}&0&c_{x}\\ 0&f_{y}&c_{y}\\ 0&0&1 \end{bmatrix} \begin{bmatrix} Xc\\ Yc\\ Zc \end{bmatrix}$ ，

其中 $f_{x}=\alpha f,f_{y}=\beta f$ ，分别称为u轴和v轴上的归一化焦距，f是相机的焦距， $\alpha$ （dX）和 $\beta$ （dY）分别表示传感器u轴和v轴上单位像素的尺寸大小，单位为mm/pixel，现代技术下一般二者相等cx和cy则表示的是光学中心，即摄像机光轴与图像平面的交点，通常位于图像中心处，故其值常取分辨率的一半。

其中 $K=\begin{bmatrix} f_{x}&0&c_{x}\\ 0&f_{y}&c_{y}\\ 0&0&1 \end{bmatrix}$ 为相机内参

世界坐标系到像素坐标系

$\begin{bmatrix} u\\ v\\ 1 \end{bmatrix}=\frac{1}{Zc}\begin{bmatrix} f_{x}&0&c_{x}&0\\ 0&f_{y}&c_{y}&0\\ 0&0&1&0 \end{bmatrix} \begin{bmatrix} Xc\\ Yc\\ Zc \\1\end{bmatrix}=\frac{1}{Zc}\begin{bmatrix} f_{x}&0&c_{x}&0\\ 0&f_{y}&c_{y}&0\\ 0&0&1&0 \end{bmatrix}\begin{bmatrix} R&t \\ 0^{T}& 1 \end{bmatrix} \begin{bmatrix} Xw\\ Yw\\ Zw \\1\end{bmatrix}$ ，

其中 $\begin{bmatrix} R &t \\ 0^{T}& 1 \end{bmatrix}$ 为相机外参，注意R，t为世界坐标到相机坐标的变换Pc=RPw+t；

2、相机畸变参数

畸变参数：

畸变（distortion）是对直线投影（rectilinear projection）的一种偏移。

简单来说直线投影是场景内的一条直线投影到图片上也保持为一条直线。

畸变简单来说就是一条直线投影到图片上不能保持为一条直线了，这是一种光学畸变（optical aberration）,可能由于摄像机镜头原因。

径向畸变与切向畸变

1、径向畸变来自于透镜形状，由于光线透过镜头的弯曲程度造成，在远离透镜中心的地方比靠近中心的地方更加弯曲，对于径向畸变，成像仪中心（光学中心）的畸变为0，随着向边缘移动，畸变越来越严重。一般包括枕形畸变、桶形畸变。

2、切向畸变来自于整个摄像机的组装过程，是由于透镜本身与成像平面不平行而产生的。

考虑畸变的情况：考虑较为明显的径向畸变和切向畸变

径向畸变矫正参数：k1,k2,k3，切向畸变矫正参数：p1,p2，一共需要考虑5个畸变参数。

3、相机标定

标定步骤：

1、打印一张棋盘格，把它贴在一个平面上，作为标定物。
2、通过调整标定物或摄像机的方向，为标定物拍摄一些不同方向的照片。
3、从照片中提取棋盘格角点。
4、估算理想无畸变的情况下，五个内参和六个外参。
5、应用最小二乘法估算实际存在径向畸变下的畸变系数。
6、极大似然法，优化估计，提升估计精度。

二、基本矩阵与对极约束

立体几何中有以下问题：

1、已知一幅图像中一点，如何寻找另一幅图像中这个点的对应点（根据是否知道相机的相对位置，此问题求解方式不同）

2、已知两幅图像中两点是对应关系，如何求解两相机的相对位置和姿态

3、已知多幅图像中同一3D点的对应点，如何求解该3D点的3D坐标

对于问题2，可以用对极几何约束，基本矩阵求解，推导与介绍如下所示

基本概念：

立体成像的基本几何就是对极几何。下图是最经典的对极几何示意图。

O1和O2为两个相机（也有可能是一个相机在不同时刻的位置）的主点，P为空间中一个物点，两个相对的白色平面是像面(严格按照光路应该是在O1 O2点的后方，与P点相反方向，CV中默认采用这种往前画的方式节省空间)。p1和p2是P点在像面上的对应点，e1 e2为像面和O1 O2的交点。O1O2为基线，也被称作相机的移动方向。有几个概念如下：

--基线：两个相机中心的连线O1O2

--对极点：e1,e2为对极点，基线与两个成像平面的角点

--对极平面：任何过基线的平面被称为对极平面，三维点P，像点p1,p2，相机中心点O1O2五个点一定在同一个对极平面上，当单位点P变化时，对极平面绕着基线旋转，形成对极平面束

--对极线：对极平面与成像平面的交线，如图e1p1,e2p2，所有的对极线相交于对极点

对极平面约束：表达了像点x和对极线的对应关系

相机1的像点p1在成像平面上的对应点p2一定在对极线l'上，因此存在一个像点p1到另一图像上的对极线l'的对应关系。基础矩阵F表示的就是这种从点到直线的映射。

基本矩阵表达式推导：

假设像点P在相机1坐标为p(x,y,z)，在相机2坐标为p'(x’,y',z')，假设相机1通过旋转平移矩阵R,t可以得到相机2，那么

p'=pR+t.

由共面几何约束，可以得到

$\underset{O2P}{\rightarrow}\cdot\left ( \underset{O1O2}{\rightarrow} \times \underset{O1P}{\rightarrow} \right )=0$ ,

将坐标点同一到相机坐标2，则有

$\underset{O2P}{\rightarrow}=p';\underset{O2O1}{\rightarrow}=t;\underset{O1P}{\rightarrow}=p'-t=Rp+t-t=Rp$ ,代入上式则有

$(p')^{T}\cdot t_{x}Rp=0$ （1）,其中 $t_{x}$ 为t的反对称矩阵(将向量叉乘表达方式变换为矩阵点乘)， $t_{x}=\begin{bmatrix} 0 & -t3& t2\\ t3&0 &-t1 \\ -t2 & t1 & 0 \end{bmatrix}$ 。

假设相机1内参为k，相机2内参为k'，将相机坐标变为像素坐标表达，对应像点分别为m,m'，由于

zm=kp,z‘m'=k'p'，其中z，z'为比例因子，代入上式（1），则有

$z'(m')^{T}(k')^{-T}\cdot [R][t_{x}] zmk^{-1}=zz'(m')^{T}(k')^{-T} [R][t_{x}] mk^{-1}=0$ ,

则有

$(m')^{T}Fm=(m')^{T}(k')^{-T} Ek^{-1}m=(m')^{T}(k')^{-T} [R][t_{x}]k^{-1}m=0$

其中 $F=(k')^{-T} [R][t_{x}] k^{-1}$ 为基础矩阵， $E= [R][t_{x}]$ 为本质矩阵

从基础矩阵到相机位姿

相机的相对位姿可以通过特征点匹配估计出来：

提取两幅图像的特征点，并进行匹配

利用匹配得像点计算两视图的基础矩阵F

已知相机内参，从基础矩阵F中分解得到相机的选择矩阵R和平移向量t

基础矩阵求解

加上有像点p1(u1,v1)，像点p1(u2,v2).则根据对极约束，有

$p1F(p2)^{T}=0$ 表达为矩阵形式如下

$\begin{bmatrix} u1&v1&1\\ \end{bmatrix}F\begin{bmatrix} u2\\ v2\\ 1 \end{bmatrix}=0$ ,其中 $F=\begin{bmatrix} f11 & f12 &f13 \\ f21 & f22 & f23\\ f31& f32&f33 \end{bmatrix}$ 为3*3的矩阵，有9个未知元素。然而，上面的公式中使用的齐次坐标，齐次坐标在相差一个常数因子下是相等，F也就只有8个未知元素，也就是说，只需要8对匹配的点对就可以求解出两视图的基础矩阵F。具体求解过程参考：https://www.cnblogs.com/wangguchangqing/p/8214032.html

opencv中使用函数findFundamentalMat(),即可解决

三、单应矩阵

基本概念：

单应(Homography)是射影几何中的概念，又称为射影变换。它把一个射影平面上的点(三维齐次矢量)映射到另一个射影平面上，并且把直线映射为直线，具有保线性质。总的来说，单应是关于三维齐次矢量的一种线性变换，可以用一个3×3的非奇异矩阵H表示。

$\begin{bmatrix} u_{1}\\ v_{1}\\ 1 \end{bmatrix}=H\begin{bmatrix} u_{2}\\ v_{2}\\ 1 \end{bmatrix}$ ,

其中， $(u1,v1,1)^{T}$ 表示图像1中的像点， $(u2,v2,1)^{T}$ 是图像2中的像点，也就是可以通过单应矩阵H将图像2变换到图像1.

单应矩阵表达式推导

假设在某平面上点X，用两个相机拍摄投影点分别为m,m'，平面在相机坐标1上单位发现了为N,则平面表达式如下

$N^{T}X1=d$ ,其中X1为点X在相机坐标1的坐标，相机2下的坐标可以表达为X2=X1R+t，则有如下表达式

$X2=RX1+t=(R\cdot \frac{1}{N^{T}}d+t)*1=(R\cdot \frac{1}{N^{T}}d+t)*\frac{N^{T}X1}{d}=(R+\frac{N^{T}}{d}t)X1$ ,

将相机坐标转为像素坐标，假设相机内参都为k则有

$m'=k(R+\frac{N^{T}}{d}t)k^{-1}m$ ,其中 $H=k(R+\frac{N^{T}}{d}t)k^{-1}$ 就是单应矩阵。

单应矩阵求解

单应性变换的目标是通过给定的几个点（通常是4对点）来得到单应性矩阵。具体推导过程参考：

https://www.zhihu.com/question/23310855

在opencv中用findHomography()求单应矩阵。

单应矩阵与基本矩阵的区别

1、两图像间的对极约束和场景的结构无关，也就是说对极约束对于任意场景结构的两幅图像都是成立的，不能给出两幅图像上的像点的一一对应关系，只能给出点对应的必要条件，另一幅图像上与图像上对应的像点在位于对应的对极线上。基础矩阵F描述的实际是一种点和直线的映射关系，而不是一种点对点的约束关系，并不能给出另一个点的确切位置。

2、平面间的单应，并不像对极约束完全不需要场景的结构信息，它对场景的结构有了要求：场景的点必须在同一个平面上，因此单应矩阵H也就能够对两图像上对应点的提供更多的约束，知道了某点在一幅图像的像点位置后，可以通过单应矩阵，求得其在另一幅图像中像点的确切位置。

参考：https://www.cnblogs.com/wangguchangqing/p/8287585.html

相机只有旋转没有平移下的单应：

$m'=kRk^{-1}m$ , $H=kRk^{-1}$ ,可由H分解得到旋转矩阵，此时基本矩阵 $F=(k')^{-T} [R][t_{x}] k^{-1}=0$ ，无法分解得到旋转矩阵。

总结：

在相机只有旋转而没有平移的情况下，两视图的对极约束就不再适用，这时可以使用单应矩阵HH来描述两个图像像点的对应关系。

在这种情况下，两图像点的匹配不依赖于三维点的深度信息，无法使用三角法重构出三维点在世界坐标系中的三维坐标。

基本矩阵，本质矩阵，单应矩阵的求解总结

8点法求基本矩阵，5点法求本质矩阵，4点法求单应矩阵。

旋转平移矩阵：本质矩阵的svd分解，与真实相差一个尺度因子。

参考：https://blog.csdn.net/xholes/article/details/79935700

四、相机姿势估计

相机位姿的三种方法：

1. 2D-2D: 特征点在同一平面或近平面时，通过Homograpy Matrix可以恢复相机位姿；当特征点的深度明显不同时则需要利用对极几何，通过求得Fundamental Matrix或者Essential Matrix来恢复相机位姿。

2.2D-3D: 通过已知的三维点，以及这些点与给定特征点的关系，恢复相机位姿，常见的是PnP。

3.3D-3D: 使用ICP对前后两帧各自的三维点进行匹配，得到两帧间的相对位姿。

从基本矩阵中恢复出相机旋转平移矩阵R，t

1、采用8点求出基本矩阵F

2、标定相机内参，得到基础矩阵E，理论上旋转平移矩阵有6个自由度，但是由于尺度等价，变为5个自由度

3、SVD分解，得到旋转平移矩阵R，t，与真实值相差一个尺度因子

SVD分解推导：

参考：https://blog.csdn.net/kokerf/article/details/72911561详细推导

参考https://www.cnblogs.com/houkai/p/6665506.html

1992年，Hartley提出了从本质矩阵在相差一个尺度因子的情况下恢复出摄像机投影矩阵的四个可能解，然后从四个解中选择一个正确解的方法。

假设 $S=[t_{x}]$ ,本质矩阵 $E=[t_{x}]R=SR$ ，有如下定理：

从本质矩阵中恢复出的相机位姿R为真实旋转矩阵，但是t为单位向量，与真实的值相差一个比例因子，在opencv3中用函数recoverPose求解得到。

注意：

“计算基础矩阵或本质矩阵”适用于特征点不共面的情况；右侧“计算单应矩阵”适用于特征点共面的情况（比如墙壁、地面、航拍等场合）。在实际应用中，如果事先无法知道特征点是否共面，则应当同时计算本质矩阵和单应矩阵，选择重投影误差比较小的那个作为最终的运动估计矩阵

2D-2D相机位姿估计的问题：

尺度不确定性
用上面的方法估计出的相机平移向量t的值并没有单位，也就是说相机移动的距离只有相对值，没有绝对值。这是单目相机固有的尺度不确定性问题，无法从根本上解决。因此单目SLAM中一般把初始化后的t归一化，即把初始化时移动的距离默认为1，此后的距离都以这个1为单位。

初始化的纯旋转问题
单目初始化不能只有旋转，必须要有一定程度的平移，否则由于t趋近于0，导致无从求解R或者误差非常大。

多于8对点的情况
如果匹配的点对数多于8（大多数情况都是这样），可以考虑充分利用这些点，而不是只从中选择8对用于计算。推荐的算法是随机采样一致性（Random Sample Consensus，RANSAC），该算法可以有效地避免错误数据对整体结果的影响。在代码中，只需要将findFundamentalMat函数的第三个参数从CV_FM_8POINT换成CV_FM_RANSAC就可以了。

链接：https://www.jianshu.com/p/fbf56587a268

【入门】（二）相机标定与矩阵求解

一、相机模型、内参、外参，畸变以及相机标定

二、基本矩阵与对极约束

三、单应矩阵

四、相机姿势估计

猜你喜欢