斜率优化DP--详解

参考资料《算法竞赛–进阶指南》

学习斜率优化前请确认你已对单调队列有了充分了解
下面我们通过这样一道题来逐步引入斜率优化

CodeVS 2212 任务安排

N个任务排成一个序列在一台机器上等待完成（顺序不得改变），这N个任务被分成若干批，每批包含相邻的若干任务。从时刻0开始，这些任务被分批加工，第i个任务单独完成所需的时间是Ti。在每批任务开始前，机器需要启动时间S，而完成这批任务所需的时间是各个任务需要时间的总和（同一批任务将在同一时刻完成）。每个任务的费用是它的完成时刻乘以一个费用系数Fi。请确定一个分组方案，使得总费用最小。
$1<=N<=5000 , 0<=S<=50$ ， $Ti,Fi$ 均为不大于100的正整数

解法1：

$dp[i][j]$ 表示前 $i$ 个任务分 $j$ 批完成的最小花费
$sumT,sumF$ 分别是 $T,F$ 的前缀和
dp方程很好想

初始化 $dp[0]=0$ ，其余为INF
$dp[i][j]=min(\ dp[k][j-1]+(j*S+sumT[i])*(sumF[i]-sumF[j])\ )$
时间复杂度为 $O(n^3)$

解法2：

$O(n^3)$ 对N<=5000来说显然会很吃力
我们发现题目并没有要求固定分批数
那么能不能把枚举批数的一维省去呢，答案是肯定的

$dp[i]$ 表示前 $i$ 个任务完成的最小花费
$dp[i]=min(\ dp[j]+sumT[i]*(sumF[i]-sumF[j])+S*(sumF[n]-sumF[j])\ )$
显然当前执行批次的启动时间S一定会累加到后面完成的批次
其中 $S*(sumF[n]-sumF[j])$ 就相当于给后面的任务完成时间都加上了S

时间复杂度为 $O(n^2)$

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cmath>
using namespace std;

int read()
{
    int x=0,f=1;
    char ss=getchar();
    while(ss<'0'||ss>'9'){if(ss=='-')f=-1;ss=getchar();}
    while(ss>='0'&&ss<='9'){x=x*10+ss-'0';ss=getchar();}
    return x*f;
}

const int maxn=5010;
int n,S;
int sumT[maxn],sumF[maxn];
int dp[maxn];

int main()
{
    n=read();S=read();
    for(int i=1;i<=n;++i)
    {
        int t=read(),f=read();
        sumT[i]=sumT[i-1]+t; sumF[i]=sumF[i-1]+f;
    }
    
    memset(dp,67,sizeof(dp)); dp[0]=0;
    for(int i=1;i<=n;++i)
    for(int j=0;j<i;++j)
    dp[i]=min(dp[i],dp[j]+sumT[i]*(sumF[i]-sumF[j])+S*(sumF[n]-sumF[j]));
    
    printf("%d",dp[n]);
    return 0;
}

POJ - 1180 Batch Scheduling

同CodeVS 2212 任务安排
$N<=10000$ ， $Ti,Fi$ 均为不大于100的正整数

这里题目范围只限定了N<=10000是想说明卡掉了 $O(n^2)$ 算法
虽然蒟蒻不知道存不存在 $O(nlogn)$ 的解法
但这里将要介绍的 $O(n)$ 算法完全可以胜任 $1e6$ 的数据

考虑将上述解法2的方程稍作变形
$dp[i]=min(\ dp[j]+sumT[i]*(sumF[i]-sumF[j])+S*(sumF[n]-sumF[j])\ )$
$dp[i]=min(\ dp[j]-(sumT[i]+S)*sumF[j]\ )+sumT[i]*sumF[i]+S*sumF[n]$
$dp[j]=(sumT[i]+S)*sumF[j]+dp[i]-sumT[i]*sumF[i]-S*sumF[n]$

现在这个式子里唯二未知的量只有 $sumF[j],dp[j]$ ，而我们要使 $dp[i]$ 最大
这不就是高中数学必修五–线性规划嘛

也就是说所有 $(sumF[j],dp[j])j\in[1,i)$ 都是一个可行点
我们将一条斜率为 $sumT[i]+S$ 的直线不断向上移
第一次接触到的可行点就是更新 $dp[i]$ 的

那么要如何确定到这个可行点呢
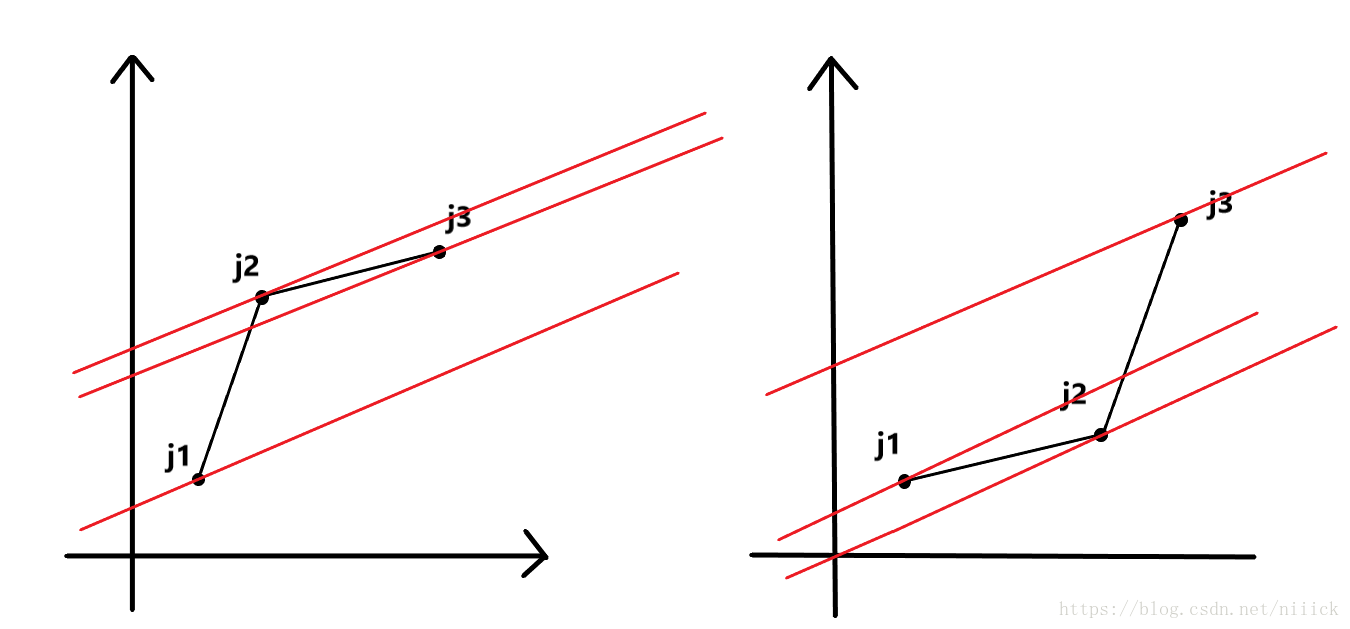
我们假设现在有三个可行点 $(sumF[j_1],dp[j_1])(sumF[j_2],dp[j_2])(sumF[j_2],dp[j_2])$ 且 $j_1<j_2<j_3$
可以知道 $sumF[j_1],sumF[j_2],sumF[j_3]$ 也是递增的
在这里插入图片描述
由于斜率 $k=sumT[i]+S$ 一定大于0
所以假如三个点构成如左图所示的上凸，那么 $j_2$ 一定不是最优的可行点
假如三个点构成如右图所示的下凸，那么 $j_2$ 有可能成为最优的可行点

形式化一点来说
当斜率 $K_{j_1j_2}=\frac{dp[j_2]-dp[j_1]}{sumF[j_2]-sumF[j_1]}<K_{j_2j_3}=\frac{dp[j_3]-dp[j_2]}{sumF[j_3]-sumF[j_2]}$ 时
$j_2$ 才有可能成为最优可行点

由此我们得到一个维护策略
即维护一个相邻两点间线段斜率单调递增的下凸壳
换句话说，我们要把那些会造成 $j_1,j_2,j_3$ 连线形成上凸的 $j_2$ 都删去
那么有可能继续更新的 $j$ 就是这个凸壳的所有顶点

保证 $j$ 的相邻连线斜率单调递增后
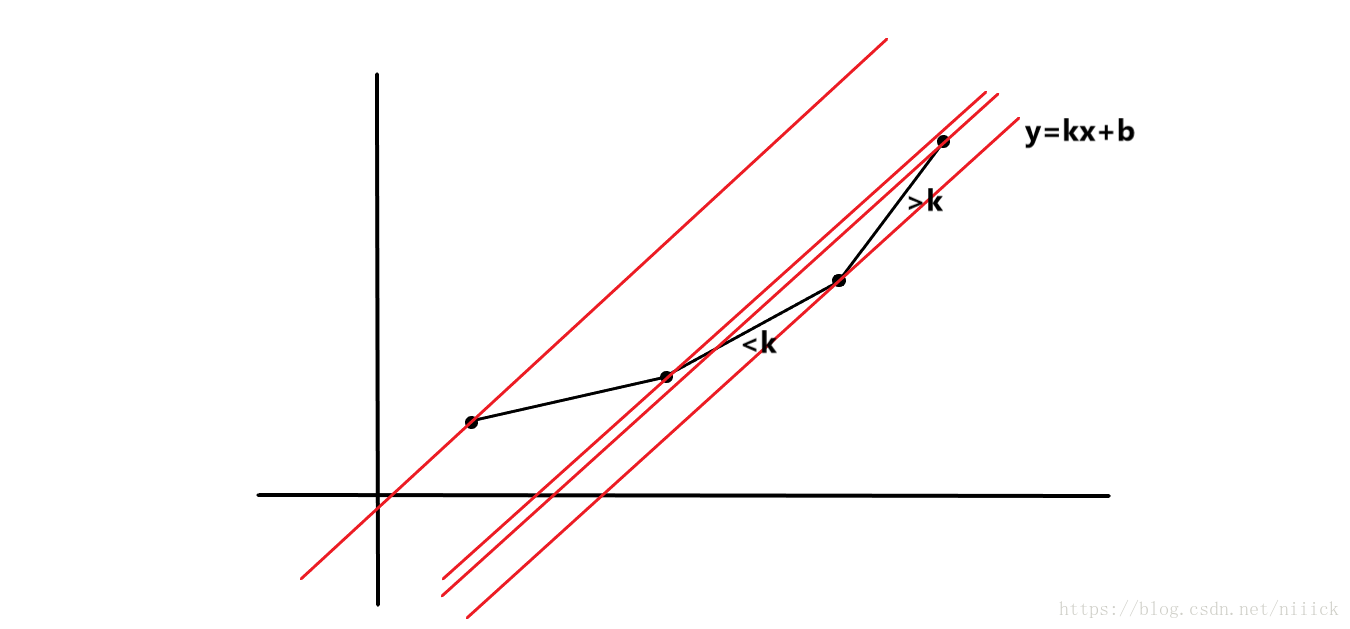
考虑对于一条斜率为 $K$ 的直线
若某个顶点 $j$ 左侧线段斜率小于 $K$ ，右侧连线大于 $K$
那么 $j$ 一定是令这条斜率为K的直线截距最小的可行点
这一点对 $K<0$ 也是成立的
在这里插入图片描述

到这里维护方式的选择已经比较明显了–单调队列
对于当前需要更新的 $dp[i]$
根据上述思路，我们只需要保留所有斜率大于 $K=S+sumT[i]$ 的连线
因为 $K$ 的单调递增，显然前面删去的点一定不可能成为更新后面dp值的最优可行点
所以每次更新前检查队头保存顶点 $j_1$ 与队头下一个顶点 $j_2$ 的斜率是否小于等于K，若是就不断弹出队首

此时队首就是能更新 $dp[i]$ 的最优可行点
更新完之后，我们在保证顶点连线斜率单调递增的情况下，使最后一个连线斜率尽量小
即不断检查当前点 $i$ 与队尾 $j$ 的斜率 $K$ 和队尾 $j$ 与队尾上一位 $j_1$ 的斜率 $K_1$
若 $K<=k_1$ ，就不断弹出队尾

时间复杂度约为 $O(n)$

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cmath>
using namespace std;

int read()
{
    int x=0,f=1;
    char ss=getchar();
    while(ss<'0'||ss>'9'){if(ss=='-')f=-1;ss=getchar();}
    while(ss>='0'&&ss<='9'){x=x*10+ss-'0';ss=getchar();}
    return x*f;
}

const int maxn=300010;
int n,S;
int sumT[maxn],sumF[maxn];
int dp[maxn];
int q[maxn],ll,rr;

int main()
{
    n=read();S=read();
    for(int i=1;i<=n;++i)
    {
        int t=read(),f=read();
        sumT[i]=sumT[i-1]+t; sumF[i]=sumF[i-1]+f;
    }
    
    //dp[0]=0;
    ll=rr=1;
    for(int i=1;i<=n;++i)
    {
    	//为了保证精度，计算斜率的除法移项后改为乘法
    	while( ll<rr && (dp[q[ll+1]]-dp[q[ll]])<=(S+sumT[i])*(sumF[q[ll+1]]-sumF[q[ll]]) ) ++ll;
    	
    	dp[i]=dp[q[ll]]-(S+sumT[i])*sumF[q[ll]]+sumT[i]*sumF[i]+S*sumF[n];
    	
    	while( ll<rr && (dp[q[rr]]-dp[q[rr-1]])*(sumF[i]-sumF[q[rr]]) >=  
		(dp[i]-dp[q[rr]])*(sumF[q[rr]]-sumF[q[rr-1]]) ) --rr;
		
		q[++rr]=i;
	}
	printf("%d",dp[n]);
    return 0;
}

BZOJ 2726[SDOI2012]任务安排

同CodeVS 2212 任务安排
$0<N<=300000 ,0<=S<=2^8$
$-(2^8)<=Ti<=2^8,0<=Fi<=2^8$

(CodeVS也有这道题，但感觉数据有点问题???没有一个通过的)

这里 $T_i$ 出现了负数，显然每次直线斜率 $K=S+sumT[i]$ 不再具有单调性
维护下凸壳的策略还是可行的
但每次从队首弹出斜率小于等于K的连线就不再正确了

由于不能从队首弹出顶点，那么每次更新的时候队首就不是最优可行点了
但单调队列内相邻顶点的连线斜率还是单调递增的
所以我们可以每次在单调队列内二分出一个顶点 $j$
使得 $j$ 左侧连线斜率小于K，右侧大于K，那么 $j$ 即为最优可行点

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cmath>
using namespace std;
typedef long long lt;
 
lt read()
{
    lt f=1,x=0;
    char ss=getchar();
    while(ss<'0'||ss>'9'){if(ss=='-')f=-1;ss=getchar();}
    while(ss>='0'&&ss<='9'){x=x*10+ss-'0';ss=getchar();}
    return f*x;
}
 
const int maxn=300010;
int n;
lt S,sumT[maxn],sumF[maxn];
lt dp[maxn];
int q[maxn],ll,rr;
 
int find(lt k)
{
    if(ll==rr) return q[rr];
    int L=ll,R=rr;
    while(L<R)
    {
        int mid=L+R>>1;
        if( dp[q[mid+1]]-dp[q[mid]] <= k*(sumF[q[mid+1]]-sumF[q[mid]]) ) L=mid+1;
        else R=mid;
    }
    return L;
}
 
int main()
{
    n=read();S=read();
    for(int i=1;i<=n;++i)
    {
        lt t=read(),f=read();
        sumT[i]=sumT[i-1]+t; sumF[i]=sumF[i-1]+f;
    }
     
    //dp[0]=0;
    ll=rr=1;
    for(int i=1;i<=n;++i)
    {
        int p=find(S+sumT[i]);
         
        dp[i]=dp[q[p]]-(S+sumT[i])*sumF[q[p]]+sumT[i]*sumF[i]+S*sumF[n];
         
        while( ll<rr && (dp[q[rr]]-dp[q[rr-1]])*(sumF[i]-sumF[q[rr]]) >=  
        (dp[i]-dp[q[rr]])*(sumF[q[rr]]-sumF[q[rr-1]]) ) --rr;
         
        q[++rr]=i;
    }
    printf("%lld",dp[n]);
    return 0;
}

CodeVS 2212 任务安排

解法1：

解法2：

POJ - 1180 Batch Scheduling

BZOJ 2726[SDOI2012]任务安排

BZOJ1010||洛谷P3195 [HNOI2008]玩具装箱TOY AND 题解

BZOJ3437 小P的牧场 AND 题解

BZOJ1911||洛谷P3628 [APIO2010]特别行动队 AND 题解

BZOJ3156 防御准备 AND 题解

猜你喜欢