树、堆
树:
1、一课树中的任意两个结点有仅有唯一的一条路径连通。
2、一棵树如果有n个结点,那么它一定恰好有n-1条边。
3、在一棵树中加一条边将会构造一个回路。
满二叉树:二叉树所有的叶结点都有同样的深度。
深度为:n,结点数:2**n - 1
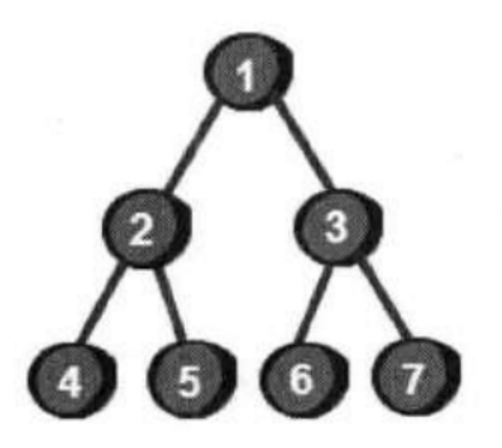
完全二叉树
如果一棵二叉树除了最右边位置上有一个或者几个叶结点缺少外,其他是丰满的,那么这样的二叉树就完全二叉树。严格的定义是:若设二叉树的高度为h,除h层外,其他各层(1~h-1)的结点数都达到最大个数,第n层从右向左连续缺若干个结点,则这个二叉树就是完全二叉树。


通过上图我们发现,如果完全二叉树的一个父结点编号为k,那么它左儿子的编号就是2*k,右儿子的编号就是2*k+1。如果已知儿子(左儿子或右儿子)的编号是x,那么它父结点的编号就是x/2,注意这里只取商的整数部分。
如果一颗完全二叉树有N个结点,那么这个完全二叉树的高度为log2N,简写logN,即最多有logN层结点。完全二叉树的最典型应用就是一个堆。
堆—神奇的优先队列
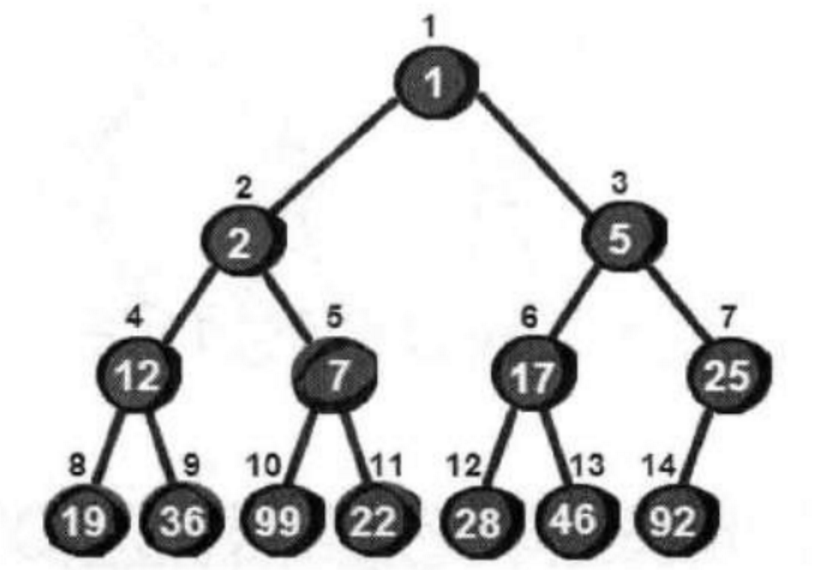
最大堆:所有父节点都比儿子结点要大;
最小堆:所有父节点都比儿子结点要小;

很显然最小的数就在堆顶,假设存储这个堆的数组叫做h的话,最小数就是h[1]。接下来,我们将堆顶的数删除。将新增加的数23放到堆顶。显然加了新数后已经不符合最小堆的特性,我们需要将新增加的数调整到合适的位置。那如何调整呢?
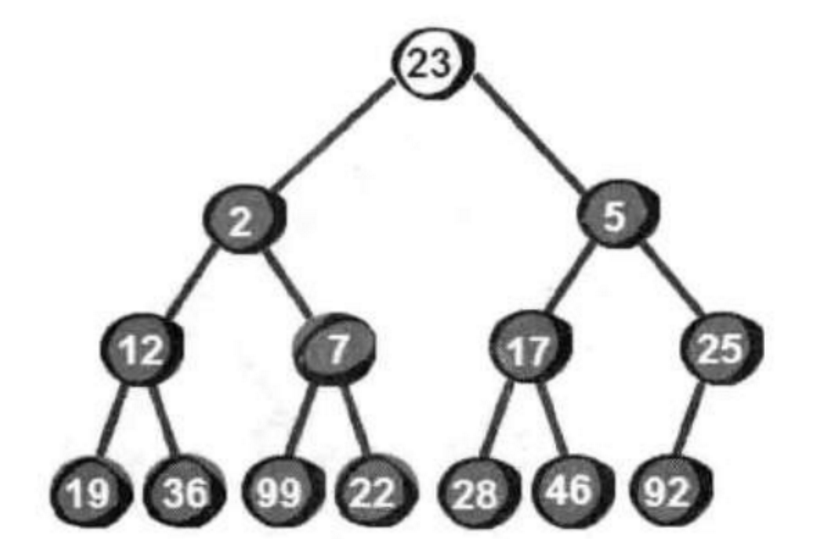
向下调整!我们需要将这个数与它的两个儿子2和5比较,选择较小的一个与它交换,交换之后如下。

我们发展此时还是不符合最小堆的特性,因此还需要继续向下调整。于是继续将23与它的两个儿子12和7比较,选择较小一个交换,交换之后如下。

至此,还是不符合最小堆的特性,仍需要继续向下调整,直到符合最小堆的特性为止。

现在我们发现已经符合最小堆的特性了。综上所述,当新增加一个数被放置到堆顶时,如果此时不符合最小堆的特性,则需要将这个数向下调整,直到找到合适的位置为止,使其重新符合最小堆的特性。

时间复杂度:logN
新增一个数:

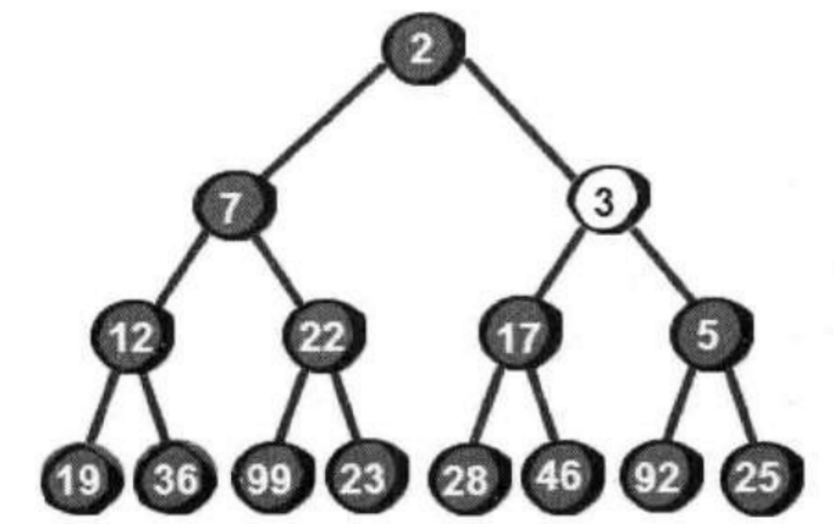
构造一个最小堆

当然目前这个棵树仍然不符合最小堆的特性,我们需要继续调整以3号结点为根的子树,即将3号结点向下调整。

同理,继续调整以2号结点为根的子树,最后调整以1号结点为根的子树。调整完毕之后,整棵树就符合最小堆的特性了。

像这样支持插入元素和寻找最大 (小)值元素的数据结构称为优先队列。如果使用普通队列来实现这两个功能,那么寻找最大元素需要枚举整个队列,这样的时间复杂度比较高。如果是已排序好的数据,那么插入一个元素则需要移动很多元素,时间复杂度度依旧很高。而堆就是一种优先队列的实现,可以很好地解决这两种操作。
另外Dijkstr算法中每次找离源点最近的一个顶点也可以用堆来优化,使算法的时间复杂度降到O((M+N)logN)。堆还经常被用来求一个数列中第K大的数,只需要建立一个大小为K的最小堆,堆顶就是第K大的数。
注:内容来源于《啊哈.算法》