《SVM笔记系列之六》支持向量机中的核技巧那些事儿

前言

我们在前文[1-5]中介绍了线性支持向量机的原理和推导，涉及到了软和硬的线性支持向量机，还有相关的广义拉格朗日乘数法和KKT条件等。然而，光靠着前面介绍的这些内容，只能够对近似于线性可分的数据进行分割，而不能对非线性的数据进行处理，这里我们简单介绍下支持向量机中使用的核技巧，使用了核技巧的支持向量机就具备了分割非线性数据的能力。本篇可能是我们这个系列的最后一篇了，如果有机会我们在SMO中再会吧。

如有谬误，请联系指正。转载请注明出处。

联系方式：
e-mail: [email protected]
QQ: 973926198
github: https://github.com/FesianXu

1. 重回SVM

我们在前文[1-5]中就线性SVM做了比较系统的介绍和推导，我们这里做个简单的小回顾。支持向量机(Support Vector Machine,SVM)，是一种基于最大间隔原则进行推导出来的线性分类器，如果引入松弛项，则可以处理近似线性可分的一些数据，其最终的对偶问题的数学表达形式为(1.1)，之所以用对偶形式求解是因为可以轻松地引入所谓的核技巧，我们后面将会看到这个便利性。
$\min_{\alpha} \frac{1}{2}\sum_{i=1}^N \sum_{j=1}^N \alpha_i \alpha_jy_iy_j(x_i \cdot x_j)- \sum_{i=1}^N\alpha_i \\ s.t. \ \sum_{i=1}^N\alpha_iy_i=0 \\ \alpha_i \geq0,i=1,\cdots,N \tag{1.1}$
其最终的分类超平面如(1.2):
$\theta(x) = \rm{sign}(\sum_{i=1}^N \alpha^*_iy_i(x_i \cdot x)+b^*) \tag{1.2}$

从KKT条件[3]中我们知道，除了支持向量SV会影响到决策面之外，其他所有的样本都是不会对决策面产生影响的，因此只有支持向量对应的 $\alpha_i^* > 0$ ，其他所有的 $\alpha_j^*$ 都是等于0的。也就是说，我们的支持向量机只需要记住某些决定性的样本就可以了。实际上，这种需要“记住样本”的方法，正是一类核方法(kernel method)。这个我们后面可能会独立一些文章进行讨论，这里我们记住，因为SVM只需要记忆很少的一部分样本信息，因此被称之为稀疏核方法(Sparse Kernel Method)[6]。

2. 更进一步观察SVM

我们这里更进一步对SVM的对偶优化任务和决策面，也即是式子(1.1)(1.2)进行观察，我们会发现，有一个项是相同作用的，那就是 $(x_i \cdot x_j)$ 和 $(x_i \cdot x)$ ，这两项都是在度量两个样本之间的距离。我们会发现，因为点积操作
$x_i \cdot x_j = ||x_i|| \cdot ||x_j|| \cdot \cos(\theta) \tag{2.1}$
在两个向量模长相同的情况下，可以知道这个点积的结果越大，两个样本之间的相似度越高，因此可以看作是一种样本之间的度量(metric)。这个我们可以理解，SVM作为一种稀疏核方法的之前就是一个核方法，是需要纪录训练样本的原始信息的。

但是，我们注意到，我们是在原始的样本特征空间进行对比这个相似度的，这个很关键，因为在原始的样本特征空间里面，样本不一定是线性可分的，如果在这个空间里面，线性SVM将没法达到很好的效果。

3. 开始我们的非线性之路

那么，我们在回顾了之前的一些东西之后，我们便可以开始我们的非线性之路了，抓好扶手吧，我们要起飞了。

3.1 高维映射

对于非线性的数据，如下图所示，显然我们没法通过一个线性平面对其进行分割。
在这里插入图片描述
当然，那仅仅是在二维的情况下我们没法对齐进行线性分割，谁说我们不能在更高的维度进行“维度打击”呢？！我们不妨把整个数据上升一个维度，投射到三维空间，我们将红色数据“拉高”，而绿色数据“留在原地”，那么我们就有了：
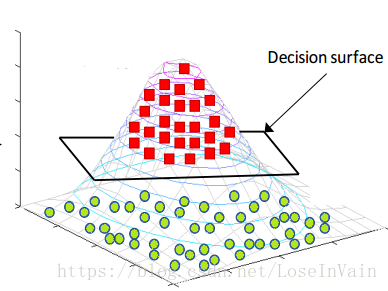
在这里插入图片描述
发现没有，在二维线性不可分的数据，在三维空间就变得线性可分了。这个时候我们可以纪录下在三维情况下的决策面，然后在做个逆操作，将其投射到原先的二维空间中，那么我们就有了:

看来这种维度打击还真是有效！

$\nabla$ 我们其实还可以再举个更为简单的例子。 $\nabla$
假如我们现在有一些数据，满足 $x_1^2+x_2^2=1$ ，是的，我们不难发现这其实就是个以原点为圆心半径为1的圆，其参数为 $x_1$ 和 $x_2$ ，但是显然的，这个是个非线性的关系，如果要转换成一个线性的关系要怎么操作呢？简单，用 $x_3 = x_1^2$ 和 $x_4 = x_2^2$ ，我们有变形等价式 $x_3+x_4=1$ ，于是我们便有了关于 $x_3$ 和 $x_4$ 的线性关系式，其关键就是映射 $\phi(x)=x^2$ 。

别小看这个例子哦，这个是我们核技巧的一个关键的直观想法哦。没晕吧？让我们继续吧。

3.2 基函数

其实我们刚才举得例子中的 $\phi(x) = x^2$ 就是一个基函数(basic function)，其作用很直接，就是将一个属于特征空间 $\mathcal{M}$ 的样本 $\mathbf{x} \in \mathcal{M}$ 映射到新的特征空间 $\mathcal{N}$ ，使得有 $\phi(\mathbf{x}) \in \mathcal{N}$ 。如果诸位看官熟悉深度学习，那么我们就会发现，其实深度学习中的激活函数无非也就是起着这种作用，将浅层的特征空间映射到深层的特征空间，使得其尽可能地容易区分。可以说，激活函数就是一种基函数。

那么我们能不能把这种映射应用到，我们刚才的第二节提到的度量测试中的原始特征空间中的样本呢？答案自然是可以的，这样，我们就会有：
$(\phi(\mathbf{x}_i) \cdot \phi(\mathbf{x_j})) \tag{3.1}$
通常为了后续讨论，我们会将式子(3.1)表示为(3.2):
$\mathcal{k}(\mathbf{x}_i, \mathbf{x}_j) = (\phi(\mathbf{x}_i) \cdot \phi(\mathbf{x_j})) = \phi(\mathbf{x}_i)^T\phi(\mathbf{x}_j) \tag{3.2}$
好的，这样我们就将原始特征空间的样本映射到新的特征空间了，这个特征空间一般来说是更高维的线性可分的空间。我们将这里的 $\mathcal{k}(\cdot, \cdot)$ 称之为核函数(kernels)，哦噢，我们的核函数正式出场了哦。

在给定了核函数的情况下，我们的对偶优化问题和决策面变成了：
$\min_{\alpha} \frac{1}{2}\sum_{i=1}^N \sum_{j=1}^N \alpha_i \alpha_jy_iy_j \mathcal{k}(x_i \cdot x_j)- \sum_{i=1}^N\alpha_i \\ s.t. \ \sum_{i=1}^N\alpha_iy_i=0 \\ \alpha_i \geq0,i=1,\cdots,N \tag{3.3 对偶问题}$
$\theta(x) = \rm{sign}(\sum_{i=1}^N \alpha^*_iy_i \mathcal{k}(x_i \cdot x)+b^*) \tag{3.4 决策面}$

但是，实际上我们是人工很难找到这个合适的映射 $\phi(\cdot)$ 的，特别是在数据复杂，而不是像例子那样的时候，那么我们该怎么办呢？我们能不能直接给定一个核函数 $\mathcal{k}(\cdot, \cdot)$ ，然后就不用理会具体的基函数了呢？这样就可以隐式地在特征空间进行特征学习，而不需要显式地指定特征空间和基函数 $\phi(\cdot)$ [9]。答案是可以的！

我们给定一个Mercer定理[10]：

如果函数 $\mathcal{k}(\cdot, \cdot)$ 是 $\mathbb{R}^n \times \mathbb{R}^n \rightarrow \mathbb{R}$ 上的映射（也就是从两个n维向量映射到实数域，既是进行样本度量计算）。那么如果 $\mathcal{k}(\cdot, \cdot)$ 是一个有效核函数（也称为Mercer核函数），那么当且仅当对于训练样例 $[x^{(1)}, x^{(2)}, \cdots, x^{(m)}]$ ，其相应的核函数矩阵是对称半正定(positive semidefinite)的，并且有 $\mathcal{k}(x,y) = \mathcal{k}(y,x)$ 。

嗯，定理很长，人生很短，这个定理说人话就是，如果这个核函数 $\mathcal{k}(\cdot, \cdot)$ 是一个对称半正定的，并且其是个对称函数（度量的基本条件），那么这个核函数就肯定对应了某个样本与样本之间的度量，其关系正如(3.2)所示，因此隐式地定义出了样本的映射函数 $\phi(\cdot)$ ，因此是个有效的核函数。

诶，但是对称半正定不是矩阵才能判断吗？这里的核函数是个函数耶？嗯…也不尽然，休息下，我们下一节继续吧。

3.3 无限维向量与希尔伯特空间

先暂时忘记之前的东西吧，清清脑袋，轻装上阵。我们在以前学习过得向量和矩阵都是有限维度的，那么是否存在无限维的向量和矩阵呢？其实，函数正是可以看成无限维的向量，想法其实很简单，假如有一个数值函数 $f:x \rightarrow y$ ，假设其定义域是整个实数，如果对应每一个输入，都输出一个输出值，我们可以把所有输出值排列起来，也就形成了一个无限维的向量，表达为 $\{y\}^{\infty}_i$ 。

而核函数 $\mathcal{k}(\mathbf{x}_i, \mathbf{x}_j)$ 作为一个双变量函数，就可以看成一个行列都是无限维的矩阵了。这样我们就可以定义其正定性了：
$\int\int f(\mathbf{x})\mathcal{k}(\mathbf{x}, \mathbf{y})f(\mathbf{y}) \rm{d} \mathbf{x} \rm{d} \mathbf{y} \geq 0 \tag{3.5}$

既然是个矩阵，那么我们就可以对其进行特征分解对吧，只不过因为是无限维，我们需要使用积分，表达式类似于矩阵的特征值分解：
$\int \mathcal{k}(\mathbf{x}, \mathbf{y}) \Phi(\mathbf{x}) \rm{d} \mathbf{x} = \lambda \Phi(\mathbf{y}) \tag{3.6}$
这里的特征就不是特征向量了，而是特征函数（看成无限维向量也可以的）。对于不同的特征值 $\lambda_1$ 和 $\lambda_2$ ，和对应的特征函数 $\Phi_1(\mathbf{x})$ 和 $\Phi_2(\mathbf{x})$ ，有：
$\begin{aligned} \int \mathcal{k}(\mathbf{x}, \mathbf{y}) \Phi_1(\mathbf{x}) \Phi_2(\mathbf{x}) \rm{d} \mathbf{x} &= \int \mathcal{k}(\mathbf{x}, \mathbf{y}) \Phi_2(\mathbf{x}) \Phi_1(\mathbf{x}) \rm{d} \mathbf{x} \\ \rightarrow \int \lambda_1 \Phi_1(\mathbf{x}) \Phi_2(\mathbf{x}) \rm{d} \mathbf{x} &= \int \lambda_2 \Phi_2(\mathbf{x}) \Phi_1(\mathbf{x}) \rm{d} \mathbf{x} \end{aligned} \tag{3.7}$
因为特征值不为0，因此由(3.7)我们有:
$< \Phi_1, \Phi_2 > = \int \Phi_1(\mathbf{x}) \Phi_2(\mathbf{x}) \rm{d} \mathbf{x} = 0 \tag{3.8}$

也就是任意两个特征函数之间是正交(Orthogonal)的，一个核函数对应着无限个特征值 $\{\lambda_i\}_{i=1}^{\infty}$ 和无限个特征函数 $\{\Phi_i\}_{i=1}^{\infty}$ ，这个正是原先函数空间的一组正交基。

回想到我们以前学习到的矩阵分解，我们知道我们的矩阵 $A$ 可以表示为：
$A = Q\Lambda Q^T \tag{3.9}$
其中 $Q$ 是 $A$ 的特征向量组成的正交矩阵， $\Lambda$ 是对角矩阵。特征值 $\Lambda_{i,i}$ 对应的特征向量是矩阵 $Q$ 的第 $i$ 列。我们看到在有限维空间中可以将矩阵表示为特征向量和特征值的组合表达。同样的，在无限维空间中，也可以定义这种分解，因此可以将核函数 $\mathcal{k}(\cdot,\cdot)$ 表示为:

$\mathcal{k}(\mathbf{x}, \mathbf{y}) = \sum_{i=0}^{\infty} \lambda_i \Phi_i(\mathbf{x}) \Phi_i(\mathbf{y}) \tag{3.10}$
重新整理下，将 $\{\sqrt{\lambda_i}\Phi_i\}_{i=1}^{\infty}$ 作为一组正交基，构建出一个空间 $\mathcal{H}$ 。不难发现，这个空间是无限维的，如果再深入探讨，还会发现他是完备的内积空间，因此被称之为希尔伯特空间(Hilbert space)[13]。别被名字给唬住了，其实就是将欧几里德空间的性质延伸到了无限维而已。

回到我们的希尔伯特空间，我们会发现，这个空间中的任意一个函数（向量）都可以由正交基进行线性表出：
$f = \sum_{i=1}^{\infty} f_i \sqrt{\lambda_i} \Phi_i \tag{3.11}$
所以 $f$ 可以表示为空间 $\mathcal{H}$ 中的一个无限维向量：
$f = (f_1, f_2, \cdots,)^T_{\mathcal{H}} \tag{3.12}$

3.4 再生性(Reproduce)

前面3.3讨论了很多关于函数在希尔伯特空间上的表出形式，我们这里在仔细观察下核函数。我们发现，其实核函数可以拆分为：
$\mathcal{k}(\mathbf{x}, \mathbf{y}) = \sum_{i=0}^{\infty}\lambda_i\Phi_i(\mathbf{x})\Phi_i(\mathbf{y}) = < \mathcal{k}(\mathbf{x},\cdot), \mathcal{k}(\mathbf{y}, \cdot) >_{\mathcal{H}} \tag{3.13}$
其中:
$\mathcal{k}(\mathbf{x}, \cdot) = (\sqrt{\lambda_1}\Phi_1(\mathbf{x}),\sqrt{\lambda_2}\Phi_2(\mathbf{x}),\cdots)^T_{\mathcal{H}} \\ \mathcal{k}(\mathbf{y}, \cdot) = (\sqrt{\lambda_1}\Phi_1(\mathbf{y}),\sqrt{\lambda_2}\Phi_2(\mathbf{y}),\cdots)^T_{\mathcal{H}} \tag{3.14}$
发现没有，(3.13)将核函数表示为了两个函数的内积，是不是很想我们的式子(3.2)了呢。我们把这种可以用核函数来再生出两个函数的内积的这种性质称之为再生性(reproduce)，对应的希尔伯特空间称之为再生核希尔伯特空间(Reproducing Kernel Hilbert Space,RKHS)，有点吓人的名词，但是如果你能理解刚才的分解，这个其实还是蛮直接的。

我们更进一步吧，如果定义一个映射 $\phi(\cdot)$ :
$\phi(\mathbf{x}) = (\sqrt{\lambda_1}\Phi_1(\mathbf{x}),\sqrt{\lambda_2}\Phi_2(\mathbf{x}),\cdots)^T \tag{3.15}$
当然这是个无限维的向量。这个映射将样本点 $\mathbf{x} \in \mathbb{R}^n$ 投射到无限维的特征空间 $\mathcal{H}$ 中，我们有：
$< \phi(\mathbf{x}), \phi(\mathbf{y}) > = \mathcal{k}(\mathbf{x}, \mathbf{y}) = \phi(\mathbf{x})^T\phi(\mathbf{y}) \tag{3.16}$
因此，我们解决了3.2中提出的问题，我们根本就不需要知道具体的映射函数 $\phi$ 是什么形式的，特征空间在哪里（我们甚至可以投射到无限维特征空间，比如我们接下来要讲到的高斯核函数），只要是一个对称半正定的核函数 $K$ ，那么就必然存在映射 $\phi$ 和特征空间 $\mathcal{H}$ ，使得式子(3.16)成立。

这就是所谓的核技巧(Kernel trick)[12]。

PS: 为了理解为什么是从原始的有限维的特征空间映射到无限维的希尔伯特空间，我们从式子(3.15)其实不难发现， $\mathbf{x} \in \mathbb{R}^n$ ， $\sqrt{\lambda_i}\Phi_i(\mathbf{x}) \in \mathbb{R}$ ，而我们的 $i \rightarrow \infty$ ，因此可以看成映射成了无限维的特征。

3.5 高斯核函数的无限维映射性质

有效的核函数，也就是对称半正定的核函数有很多，而且有一定的性质可以扩展组合这些核函数[6]，这一块内容比较多，我们以后独立一篇文章继续讨论。这里我们主要看下使用最多的核函数，高斯核函数，也经常称之为径向基函数。

高斯核函数的数学表达形式如下所示：
$\mathcal{k}(\mathbf{x}, \mathbf{y}) = \exp(-||\mathbf{x}-\mathbf{y}||^2/2\sigma^2) \tag{3.17}$
我们现在对(3.17)进行变形(这里为了方便假设 $\mathbf{x},\mathbf{y}$ 是一维的)：
$\begin{aligned} \exp(-||x-y||^2/2\sigma^2) &= \exp(-\lambda||x-y||^2) \\ &= \exp(-\lambda x^2+2\lambda xy-\lambda y^2) \\ &= \exp(-\lambda x^2) \exp(-\lambda y^2) \exp(2\lambda xy) \end{aligned} \tag{3.18}$
利用泰勒展开[14]对式子(3.18)中的 $\exp(2\lambda xy)$ 进行展开，有:
$\begin{aligned} \exp(2\lambda xy) &= \sum_{i=1}^{\infty} \dfrac{(2\lambda xy)^i}{i!} \\ &= \sum_{i=1}^{\infty} \sqrt{\dfrac{2^i \lambda}{i!}}x \cdot \sqrt{\dfrac{2^i \lambda}{i!}}y \end{aligned} \tag{3.19}$
现在结合(3.18)和(3.19)，我们有：
$\begin{aligned} \exp(-||x-y||^2&/2\sigma^2) \\ &= \sum_{i=1}^{\infty} \sqrt{\dfrac{2^i \lambda}{i!}} \exp{(-\lambda x^2)}x \cdot \sqrt{\dfrac{2^i \lambda}{i!}} \exp{(-\lambda y^2)}y \end{aligned} \tag{3.20}$
用序列 $\mathbf{x} = \{\sqrt{\dfrac{2^1 \lambda}{1!}} \exp{(-\lambda x^2)}x, \sqrt{\dfrac{2^2 \lambda}{2!}} \exp{(-\lambda x^2)}x, \cdots\}$ , $\mathbf{y}=\{\sqrt{\dfrac{2^1 \lambda}{1!}} \exp{(-\lambda y^2)}y, \sqrt{\dfrac{2^2 \lambda}{2!}} \exp{(-\lambda y^2)}y,\cdots\}$
这两个都是无限维向量，也即是一个映射函数 $\phi(\cdot)$ 。于是式子(3.20)可以改写为:
$\exp(-||x-y||^2/2\sigma^2) = \mathbf{x}^T \mathbf{y} = \phi(\mathbf{x})^T \phi(\mathbf{y}) \tag{3.21}$
看，我们常用的高斯核函数正是一个无限维映射的核函数。

4. 总结

我们前面对再生核希尔伯特空间进行了简单的介绍，同时了解了无限维映射的核函数，高斯核函数，事实上，我们原始的SVM对偶问题推导中的 $(x_i \cdot x_j)$ 也可以看成一种核函数，只不过这是个线性核函数而已，映射到了原始的特征空间，有：
$\mathcal{k}(\mathbf{x}, \mathbf{y}) = \mathbf{x}^T \mathbf{y} \tag{4.1}$
在后续的文章中，我们将会介绍更多的核函数，如多项式核函数对数sigmoid核函数等，同时在后续的文章中，我们也将继续探讨关于基函数的一些应用。

Reference

[1]. 《SVM笔记系列之一》什么是支持向量机SVM
[2]. 《SVM笔记系列之二》SVM的拉格朗日函数表示以及其对偶问题
[3]. 《SVM笔记系列之三》拉格朗日乘数法和KKT条件的直观解释
[4]. 《SVM笔记系列之四》最优化问题的对偶问题
[5]. 《SVM笔记系列之五》软间隔线性支持向量机
[6]. Bishop C M. Pattern recognition and machine learning (information science and statistics) springer-verlag new york[J]. Inc. Secaucus, NJ, USA, 2006.
[7]. Zhang T. An introduction to support vector machines and other kernel-based learning methods[J]. AI Magazine, 2001, 22(2): 103.
[8]. Everything You Wanted to Know about the Kernel Trick
[9]. 李航. 统计学习方法[J]. 2012.
[10]. 核函数（Kernels）
[11]. 机器学习中的数学(5)-强大的矩阵奇异值分解(SVD)及其应用
[12]. A Story of Basis and Kernel – Part II: Reproducing Kernel Hilbert Space
[13]. Hilbert space
[14]. 函数的泰勒(Taylor)展开式