[Luogu P2680] [BZOJ 4326] [NOIP 2015 tg]运输计划

题目背景

公元 $2044$ 年,人类进入了宇宙纪元。

题目描述

L 国有 $n$ 个星球，还有 $n-1$ 条双向航道，每条航道建立在两个星球之间，这 $n-1$ 条航道连通了 L 国的所有星球。

小 P 掌管一家物流公司，该公司有很多个运输计划，每个运输计划形如：有一艘物流飞船需要从 $u_i$ 号星球沿最快的宇航路径飞行到 $v_i$ 号星球去。显然，飞船驶过一条航道是需要时间的，对于航道 $j$ ，任意飞船驶过它所花费的时间为 $t_j$ ，并且任意两艘飞船之间不会产生任何干扰。

为了鼓励科技创新， L 国国王同意小 P 的物流公司参与 L 国的航道建设，即允许小 P 把某一条航道改造成虫洞，飞船驶过虫洞不消耗时间。

在虫洞的建设完成前小 $P$ 的物流公司就预接了 $m$ 个运输计划。在虫洞建设完成后，这 $m$ 个运输计划会同时开始，所有飞船一起出发。当这 $m$ 个运输计划都完成时，小 P 的物流公司的阶段性工作就完成了。

如果小 P 可以自由选择将哪一条航道改造成虫洞，试求出小 P 的物流公司完成阶段性工作所需要的最短时间是多少？

输入输出格式

输入格式：

第一行包括两个正整数 $n, m$ ，表示 L 国中星球的数量及小 P 公司预接的运输计划的数量，星球从 $1$ 到 $n$ 编号。

接下来 $n-1$ 行描述航道的建设情况，其中第 $i$ 行包含三个整数 $a_i, b_i$ 和 $t_i$ ，表示第 $i$ 条双向航道修建在 $a_i$ 与 $b_i$ 两个星球之间，任意飞船驶过它所花费的时间为 $t_i$ 。数据保证 $1 \leq a_i,b_i \leq n$ 且 $0 \leq t_i \leq 1000$ 。

接下来 $m$ 行描述运输计划的情况，其中第 $j$ 行包含两个正整数 $u_j$ 和 $v_j$ ，表示第 $j$ 个运输计划是从 $u_j$ 号星球飞往 $v_j$ 号星球。数据保证 $1 \leq u_i,v_i \leq n$

输出格式：

一个整数，表示小 PP 的物流公司完成阶段性工作所需要的最短时间。

输入输出样例

输入样例#1：

输出样例#1：

说明

所有测试数据的范围和特点如下表所示

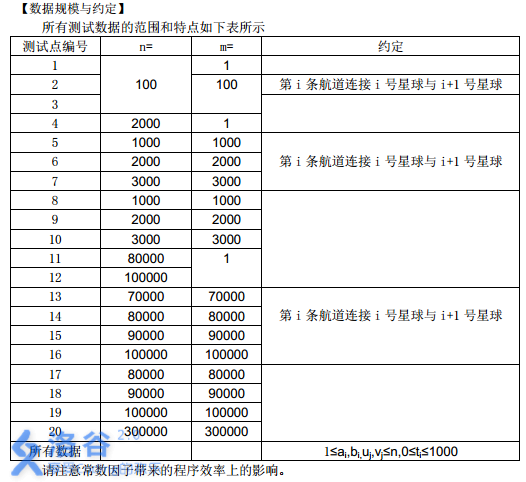
请注意常数因子带来的程序效率上的影响。

解题分析

看到这是求一个最大值的最小值，显然就可以二分，将这种最值问题转化为判定性的问题。

我们二分出答案，就可以一遍求出哪些路径的中包含的边应该被删掉。我们如何快速找到这些路径中公共的边？显然可以在树上打标记，一条 $u\to v$ 的边可以将 $u$ 和 $v$ 的权值++，在 $lca(u,v)$ 的权值 $-2$ ，这样我们从下往上递推，如果某个点的权值正好等于包含的边的数量，而且其上方的一条边的权值 $>$ 所有路径长度的最大值 $-$ 二分得到的答案，那么这种方案就是合法的。

代码如下：

#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <algorithm>
#include <cctype>
#include <cmath>
#define R register
#define IN inline
#define W while
#define gc getchar()
#define MX 300050
template <class T>
IN void in(T &x)
{
	x = 0; R char c = gc;
	for (; !isdigit(c); c = gc);
	for (;  isdigit(c); c = gc)
	x = (x << 1) + (x << 3) + c - 48;
}
int head[MX], dep[MX], son[MX], topf[MX], fat[MX], siz[MX], d[MX];
int from[MX], to[MX], dis[MX], sum[MX], lca[MX], eval[MX], ord[MX];
int dot, line, tot, cnt, mpat, msin;
struct Edge {int to, val, nex;} edge[MX << 1];
IN void add(R int fr, R int to, R int val) {edge[++cnt] = {to, val, head[fr]}, head[fr] = cnt;}
void DFS(R int now)
{
	siz[now] = 1;
	for (R int i = head[now]; i; i = edge[i].nex)
	{
		if(edge[i].to == fat[now]) continue;
		dep[edge[i].to] = dep[now] + 1; d[edge[i].to] = d[now] + edge[i].val;
		fat[edge[i].to] = now; eval[edge[i].to] = edge[i].val;
		DFS(edge[i].to); siz[now] += siz[edge[i].to];
		if(siz[edge[i].to] > siz[son[now]]) son[now] = edge[i].to;
	}
	ord[++tot] = now;
}
void DFS(R int now, R int grand)
{
	topf[now] = grand;
	if(!son[now]) return;
	DFS(son[now], grand);
	for (R int i = head[now]; i; i = edge[i].nex)
	{
		if(edge[i].to == fat[now] || edge[i].to == son[now]) continue;
		DFS(edge[i].to, edge[i].to);
	}
}
IN int get(R int x, R int y)
{
	W (topf[x] ^ topf[y])
	{
		if(dep[topf[x]] < dep[topf[y]]) std::swap(x, y);
		x = fat[topf[x]];
	}
	return dep[x] < dep[y] ? x : y;
}
IN bool check(R int ans)
{
	std::memset(sum, tot = 0, sizeof(sum));
	for (R int i = 1; i <= line; ++i) if(dis[i] > ans)
	sum[from[i]]++, sum[to[i]]++, sum[lca[i]] -= 2, ++tot;
	for (R int i = 1; i <= dot; ++i)
	{
		sum[fat[ord[i]]] += sum[ord[i]];
		if(eval[ord[i]] >= mpat - ans && sum[ord[i]] == tot) return true;
	}
	return false;
}
IN void solve(R int lef, R int rig)
{
	R int mid, ans;
	W (lef <= rig)
	{
		mid = lef + rig >> 1;
		if(check(mid)) ans = mid, rig = mid - 1;
		else lef = mid + 1;
	}
	printf("%d", ans);
}
int main(void)
{
	int a, b, c;
	in(dot), in(line);
	for (R int i = 1; i < dot; ++i)
	in(a), in(b), in(c), add(a, b, c), add(b, a, c), msin = std::max(msin, c);
	DFS(1); DFS(1, 1);
	for (R int i = 1; i <= line; ++i)
	{
		in(from[i]), in(to[i]);
		lca[i] = get(from[i], to[i]);
		dis[i] = d[from[i]] + d[to[i]] - (d[lca[i]] << 1);
		mpat = std::max(mpat, dis[i]);
	}
	solve(0, mpat);
}