支持向量机（SVM）三

支持向量机（SVM）

标签（空格分隔）： 监督学习

---

@author : [email protected]
@time : 2016-07-31

---

---

---

三、基于核函数的非线性SVM

使用上面提到的 软间隔最大化分类器 在一定程度上，可以解决非线性可分问题。但是，其实质上是用一个线性的决策面，在允许部分训练样本点出现分类错误的前提下，得到的SVM。软间隔最大化分类器 对于数据是近似线性可分的情况，效果还是不错的，但是对于完全的线性不可分的情况，其分类效果就不太好了。此时，就需要通过某种手段，将SVM从线性分类器扩展成为非线性分类器，而这个手段，就是“核技巧”。

核技巧在机器学习中的应用是非常的广泛的，特别是从2000年之后，各个大牛们对核技巧的研究也越来越深入，这里仅仅对核技巧做一些简单的说明，方便在SVM中使用，后面会使用专门的文章来详细讨论核技巧。

在前面对SVM的推导中，最后得到的判别函数为：

$$f(x)=sign\{\sum_{i=1}^N\{\alpha_i^* t_i <\phi(x_i),\phi(x)>\} + b^*\}$$

上式中有两个东西需要格外注意，$\phi(x_i)$和<\phi(x_i),\phi(x)>

$\phi(x_i)$所代表的就是一种空间映射，是核技巧必备的一个元素，这也是为什么本文从一开始推导SVM的公式的时候，使用的就是$\phi(x)$而不是单纯的$x$的原因。

$<\phi(x_i),\phi(x)>$ 指的是 $\phi(x_i),\phi(x)$ 的內积。这里可以看到，SVM的判别函数最终变成了$\phi(x_i),\phi(x)$的內积的求解。

实际上，这两点，就是核技巧的核心，下面分别对这两点进行说明：

---

3.1 特征映射解决非线性可分问题

一般来说，如果能用一个超曲面将正负训练样本完全分开，则称这种问题为非线性可分问题。

非线性可分问题一般是非常的难求的，对于近似线性可分的非线性可分问题，还可以考虑使用上面的 软间隔最大化的SVM来得到一个分类器，但是如果数据非线性十分的强，以至于无法近似线性分开的时候，我们一般就考虑对数据空间做一个空间变换，将维度提升，在低维空间中非线性可分的问题，在高维空间中可能变成线性可分的问题，在高维空间中训练一个线性分类器，对数据进行分类。

注意：维度提升后，在高维空间，是可能变成线性可分！！！是可能！！！，说白了，数据从低维空间映射到高维空间之后，到底会成什么状态，没人说得准。虽然从低维到高维之后，数据是否线性可分，存在不确定性，但也不失为一种有效的手段，并且，其在实际的应用中表现的也还不错。这个就像深度学习算法一样，那货到底干了什么事情，没人说得准，反正最终效果还不错。

提升维度的过程大致可以从下面这个例子中看出来：

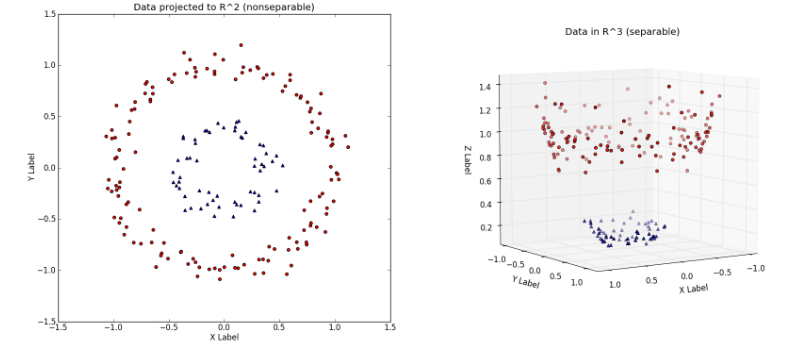
左图中对应的就是原始数据，显然左图中的数据是线性不可分的。然后通过映射：

$$[x_1,x_2]=>[x_1,x_2,x_1^2+x_2^2]$$

将数据从原始特征空间映射到新的特征空间。即，原始特征空间$X$是二维的,$X$中的样本点可以用$[x_1,x_2]$来表示，新的特征空间$Z$是三维的，$Z$中的样本点可以用$[z_1,z_2,z_3]$来表示。这样，上面的映射过程，就可以表示为：

$$z_1=x_1\\ z_2=x_2\\ z_3=x_1^2+x_2^2$$

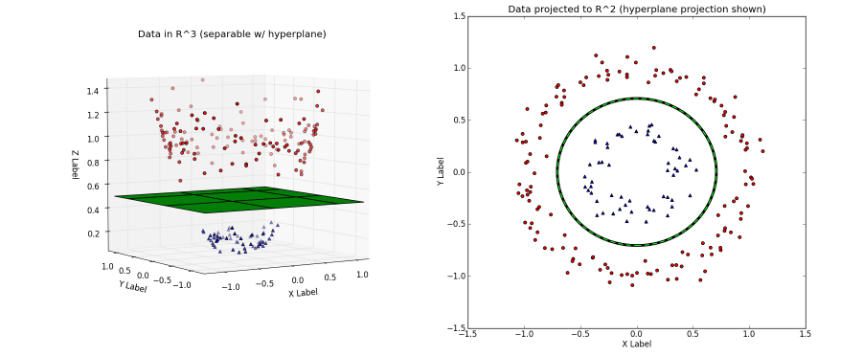
左图对应的是新的空间中，用一个平面就将变换后的数据分开；右图则对应原始空间中需要一个分线性的决策面，才可以将数据分开。

可以很容易的看出，在新的特征空间$Z$中，数据已经是线性可分的了。这就是提升数据维度，使得原空间的分线性可分问题变成新空间的线性可分问题的过程。

上面的例子说明，用线性模型求解非线性分类问题分为两个步骤：1、首先使用一个变换，将原空间的数据$X$映射到更高维度的新空间$Z$；2、在新的数据空间$Z$中,用线性分类学习方法，从训练数据中学习模型。

---

3.2 核函数$K(x_1,x_2)$

前面也提到过，在前面对SVM的推导中，最后得到的判别函数为：

$$f(x)=sign\{\sum_{i=1}^N\{\alpha_i^* t_i <\phi(x_i),\phi(x)>\} + b^*\}$$

从公式中可以明显看出，对这个判别函数的求解最终变成了对$<\phi(x_i),\phi(x)>$的计算。这里的$\phi(x)$就是上面提到的特征变换，用于解决非线性可分的问题。

按照一般的思维方式，要求解$<\phi(x_i),\phi(x)>$，那么，就需要我们先定义$\phi(x)$，再根据$x_i,x$，分别计算出 $\phi(x_i),\phi(x)$，最后计算出它们的內积。

这是一个非常繁琐的步骤，而且，由于对高维空间具体的数据分布知之甚少，我们并不能确定一个映射$\phi(x)$是否一定能够使得原始数据在高维空间中线性可分，所以一般也很难确具体的映射公式定$\phi(x)$；或者说，我们一般很难显式的定义出$\phi(x)$。

既然如此，是否可以将$<\phi(x_i),\phi(x)>$直接看成一个函数，不显式的定义$\phi(x)$，而是给定了$x_i,x$后，就直接将$<\phi(x_i),\phi(x)>$计算出来的方法呢？有！这就是核函数！！！！

核函数的定义：假设，将原始的输入空间为$X$（可能是欧式空间 $R^n$ 或者是一个离散集合），新的特征空间为$Z$(希尔伯特空间)，如果存在一个从$X$到$Z$的映射：

$$\phi(x): X\to Z$$

使得对所有的$x_1,x_2 \in X$,函数$K(x_1,x_2)$满足条件：

$$K(x_1,x_2)=<\phi(x_1),\phi(x_2)>$$

则称$K(x_1,x_2)$为一个核函数。其中$\phi(x)$为映射函数，$<\phi(x_1),\phi(x_2)>$为$\phi(x_1),\phi(x_2)$的內积。

基于前面的讨论，可以得出结论:核技巧的想法就是，在学习与预测中，仅仅定义核函数$K(x_1,x_2)$，而不显式的定义映射函数$\phi(x)$。

一般来说，直接计算$K(x_1,x_2)$相对比较容易，而通过<\phi(x_1),\phi(x_2)>的计算反而比较的复杂。

映射函数$\phi(x)$一般是将原始空间的维度升高，有时候会变成无穷维度。

---

3.3 非线性映射定$\phi(x)$与核函数$K(x_1,x_2)$的关系

• 对于给定的函数$K(x_1,x_2)$，其映射后的空间$Z$，可以使多样的，即可以映射到不同的特征空间中
• 对于给定的函数$K(x_1,x_2)$，即便映射到相同维度的特征空间，其映射函数$\phi(x)$也存在多样性

为了说明上面这两个特点，这里举个例子：假设，输入空间是$X=R^2$,核函数是$K(x_1,x_2)=(x_1*x_2)^2$
1. 取特征空间$Z=R^3$，即维度升高一个维度，此时$\phi(x)$可以取：

$$\phi(x)=[(x^{(1)})^2,\sqrt{2} x^{(1)}x^{(2)},(x^{(2)})^2]^T$$

或者也可以取：

$$\phi(x)=\frac{1}{\sqrt{2}}[(x^{(1)})^2-(x^{(2)})^2,2 x^{(1)}x^{(1)},(x^{(1)})^2+(x^{(2)})^2]^T$$

1. 取特征空间$Z=R^4$，即维度升高两个维度，此时$\phi(x)$可以取：

$$\phi(x)=[(x^{(1)})^2,x^{(1)}x^{(2)},x^{(1)}x^{(2)},(x^{(2)})^2]^T$$

---

3.4 常用的核函数

此处本应该讲讲，如何来构造核函数的，但是这个知识点实在是太过复杂，直接放在后面专门讲核技巧的文章中。

一个函数是否能称为核函数，是有非常严格的要求的，但是，我们在实际的使用中，一般都会使用一些常用的核函数，这里提供四个最常用的核函数，关于这些常用核函数的说明，也将放在后面专门讲核函数的文章中。

1.Polynomial 核函数：

$$K(x,z)=(x,z)^d;d \in N$$

2.Gaussian 核函数：

$$K(x,z)=exp(-\frac{||x-z||^2}{2\sigma^2});\sigma > 0$$

3.Sigmoid 核函数：

$$K(x,z)=tanh(\alpha <x,z>+\beta);\alpha>0,\beta>0$$

4.RBF 核函数：

$$k(x,z)=exp(-\rho d(x,z));\rho > 0,d(x,z)是任意的距离度量$$

---

3.5 对无穷维度的定性理解

每次在读一些关于核函数的书籍或者网上的博客的时候，总是会提到：核函数不需要显示的定义特征空间$Z$以及特征映射$\phi(x)$，使得学习算法隐式的在高维的特征空间中进行，甚至可以在无穷维度中进行。

这句话的前部分，已经说明过了，核函数的确不需要显示的定义特征空间$Z$以及特征映射$\phi(x)$，就是可以完成学习过程。但是，甚至可以在无穷维度中进行到底是怎么回事？我所看到的书籍和网络博客中，却没有进一步的讨论。我在这里做一个简略的说明，这需要会涉及一些核函数构造的知识，比较复杂，这里仅仅做定性的分析，详细的讨论也会放在后面专门讲解核技巧的文章中。

在高等数学中，有无穷级数的概念，举个简单的例子：

$$exp(x)=\sum_{n=0}^{\infty}{\frac{x^n}{n!}};-\infty<x<\infty$$

根据上面这个无穷级数的式子，可以很容易的推断出，指数型的核函数，可以变成无穷维度的多项式映射的结果：

$$k(x,z)=exp(k_1(x,z))\\ =\sum_{m=0}^{\infty}\frac{(k_1(x,z))^m}{m!}$$

对于Gaussian 核函数:

$$K(x,z)=exp(-\frac{||x-z||^2}{2\sigma^2});\sigma > 0$$

由于这是一个指数型的核函数，根据前面的讨论，可以定性的判断出，基于无穷级数，Gaussian 核函数的映射函数，可以是无穷维度的。其具体的公式会在后面专门讲核函数的文章中说明，这里仅仅是一个定性的理解。

下面，以一分代码来说明一下SVM的应用：

# -*- coding: utf-8 -*-

"""
@author: [email protected]
@time: 2015-07-17_13-59

SVM分类算法示例

为了绘图方便，这里仅仅使用iris数据集的前两个特征作为样本特征

LinearSVC 使用的是平方合页损失
SVC（kernel=‘linear’） 使用的是正则化合页损失

LinearSVC 使用留一法（one-vs-rest）处理多类问题
SVC 使用的是one-vs-one的方法处理多类问题

从图中很容易看出one-vs-rest方法和one-vs-one所产生的决策面的区别

"""

print __doc__

import numpy as np
import matplotlib.pyplot as plt

from sklearn import svm, datasets

# 导入iris数据
# 这个数中一共有三个类别
# 每个类别50个样本
# 每个样本有四个特征
iris = datasets.load_iris()
X = iris.data[:, [2, 3]] # 这里仅仅两个特征作为样本特征
y = iris.target

C = 1.0 # SVM正则化参数

# 使用线性核学习SVM分类器
svc = svm.SVC(kernel='linear', C=C).fit(X, y)
# 直接使用线性SVM分类器
linear_SVC = svm.LinearSVC(C=C).fit(X, y)
# 使用rbf（径向基）核学习SVM分类器
rbf_svc = svm.SVC(kernel='rbf', gamma=0.7, C=C).fit(X, y)
# 使用多项式核学习SVM分类器
poly_svc = svm.SVC(kernel='poly', degree=3, C=C).fit(X, y)

# 生成绘图用的网格
x0_min, x0_max = X[:, 0].min() - 1, X[:, 0].max() + 1
x1_min, x1_max = X[:, 1].min() - 1, X[:, 1].max() + 1

xx0, xx1 = np.meshgrid(np.arange(x0_min, x0_max, 0.02),
                       np.arange(x1_min, x1_max, 0.02))

titles = ['SVC with linear kernel',
          'LinearSVC',
          'SVC with RBF kernel',
          'SVC with polynomial kernel']

color = ['r']*50 + ['g']*50 + ['b']*50

for i, clf in enumerate((svc, linear_SVC, rbf_svc, poly_svc)):
    plt.subplot(2, 2, i + 1)
    plt.subplots_adjust(wspace=0.4, hspace=0.4)

    z = clf.predict(np.c_[xx0.ravel(), xx1.ravel()])
    z = z.reshape(xx0.shape)

    plt.contourf(xx0, xx1, z, cmap=plt.cm.Paired, alpha=0.8)
    plt.scatter(X[:, 0], X[:, 1], c=color)

    plt.xlabel('feature_1')
    plt.ylabel('feature_2')
    plt.xlim(xx0.min(), xx0.max())
    plt.ylim(xx1.min(), xx1.max())
    plt.title(titles[i])

plt.show()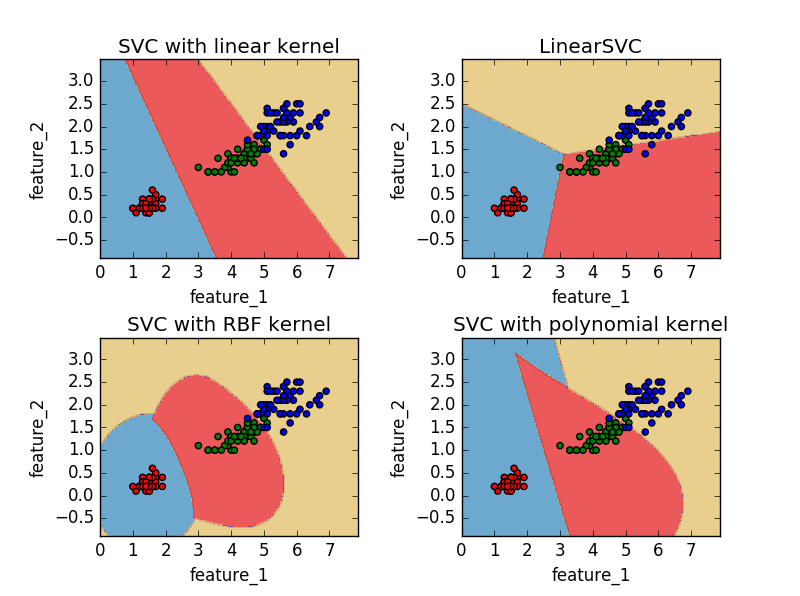

---

---

其实，关于SVM算法，如果是入门，看到这个地方，就已经不用再往下深究了。后面是SMO算法的推导，如果不清楚，并不影响SVM的理解。

---

---