最近遇到一个题,就是给两个数,这两个数有无限个,问你由这些数能得到哪些数。
还可以扩展成有n个数,问你能得到哪些数
这里其实是有一个结论的,就是:
①两个数互质,就可以生成很多很多数,而且从某个数开始就是连续的
②两个数不互质,生成的数一定是gcd(a,b)的倍数,gcd(a,b)就表示两个数的最小公倍数。
那么显然如果不互质,产生的数肯定没第一种情况多的。
关于更多的结论,下面会慢慢列举。
那么会遇到些什么样的题目呢?
我们看一下
下面是一道蓝桥杯的题,但是感觉出的还不错。
小明几乎每天早晨都会在一家包子铺吃早餐。他发现这家包子铺有N种蒸笼,其中第i种蒸笼恰好能放Ai个包子。每种蒸笼都有非常多笼,可以认为是无限笼。
每当有顾客想买X个包子,卖包子的大叔就会迅速选出若干笼包子来,使得这若干笼中恰好一共有X个包子。比如一共有3种蒸笼,分别能放3、4和5个包子。当顾客想买11个包子时,大叔就会选2笼3个的再加1笼5个的(也可能选出1笼3个的再加2笼4个的)。
当然有时包子大叔无论如何也凑不出顾客想买的数量。比如一共有3种蒸笼,分别能放4、5和6个包子。而顾客想买7个包子时,大叔就凑不出来了。
小明想知道一共有多少种数目是包子大叔凑不出来的。
输入
----
第一行包含一个整数N。(1 <= N <= 100)
以下N行每行包含一个整数Ai。(1 <= Ai <= 100)
输出
----
一个整数代表答案。如果凑不出的数目有无限多个,输出INF。
例如,
输入:
2
4
5
程序应该输出:
6
再例如,
输入:
2
4
6
程序应该输出:
INF
样例解释:
对于样例1,凑不出的数目包括:1, 2, 3, 6, 7, 11。
对于样例2,所有奇数都凑不出来,所以有无限多个
我们看一下题解:
做法:这是扩展欧几里德变形的,有个定理。
如果满足所有数的最大公约数不为1则有无穷个,
否则都是有限个。然后利用完全背包就可以统计了。
#include <algorithm>
#include <string.h>
#include <iostream>
#include <stdio.h>
#include <string>
#include <vector>
#include <queue>
#include <map>
#include <set>
using namespace std;
int gcd(int a,int b){
if(b == 0) return a;
return gcd(b,a%b);
}
int arr[110],n;
const int N = 10010;
bool bk[N];
int main()
{
scanf("%d",&n);
for(int i = 0 ; i < n ; i ++)
scanf("%d",&arr[i]);
int g = arr[0];
for(int i = 1 ; i < n ; i ++)
g = gcd(g,arr[i]);
if(g != 1)
{
printf("INF\n");
}else{
bk[0] = true;
for(int i = 0 ; i < n ; i ++)
{
for(int j = 0 ; j + arr[i] < N ; j ++)
if(bk[j])bk[j+arr[i]]= true;
}
int count = 0;
for(int i = N-1 ; i >= 0 ; i --){
if(bk[i] == false) count++;
}
printf("%d\n",count);
}
return 0;
}对于代码里面完全背包的那里,我想解释一下,
n就是表示蒸笼的种类数,N是最大体积,也就相当于有1-n号物品,它们的体积不一样,有无限个,问你能凑出哪些体积,
那么我们就两层for循环就能解决问题了。
顺便说一下,通过上面的背包解法,我发现了个小规律,两个数互质的情况下,最后一个凑不出的数为 a*b-(a+b)
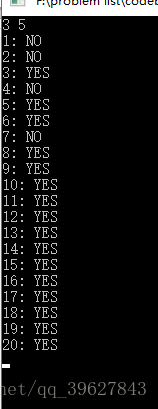
我们看看截图:
3 和5最后一个凑不出来的数为7, 从7后面的数都可以凑出来,而 7=3*5-(3+5)
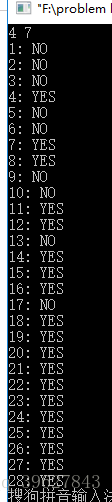
我们再看一个
4和7最后一个凑不出来的数为 17 而 17=(4*7)-(4+7)
但是,其实这个小结论还没用过,嘻嘻,所以也不用记了,到时候打表找找规律吧。
然后,做到后来,才发现此类体型是拓展欧几里得的题目
先看看拓展欧几里得的模板
ll x,y;
ll exGcd(int a,int b)
{
if(b==0)
{
x = 1;
y = 0;
return a;
}
ll ans = exGcd(b,a%b);
ll t = x; x = y;
y = t-a/b*y;
return ans;
}那么这个函数是干啥的呢,他是用来求不定方程的解的
exGcd这个函数范围的是a和b的gcd,但是x,和y才是最重要的,x,y是全局变量,表示方程ax+by=gcd(a,b)的解
那么有人可能会问,只能解这一个方程,用它干嘛,其实并不是,我们通过两边同乘以某个数,就可以得到任意方程的解。
唯一的限制条件是:所有的数必须是整数。
那么我们来看看:
exgcd 解不定方程
对于 ax+by=c 的不定方程,设 r=gcd(a,b)
当 c%r!=0 时无整数解
当 c%r=0 时,将方程右边 *r/c 后转换为 ax+by=r 的形式
可以根据扩展欧几里得算法求得一组整数解 x0 , y0
而这只是转换后的方程的解,原方程的一组解应再 *c/r 转变回去
(如 2x+4y=4 转换为 2x+4y=2 后应再将解得的 x , y 乘上2)
则原方程解为 x1=x0*c/r , y1=x0*c/r (乘以c/r)
通解 x=x1+b/r*t , y=y1-a/r*t ,其中 t 为整数
注意,y的通解是减号---
那么我们就直接看题:
ZOJ 3593
There is an interesting and simple one person game. Suppose there is a number axis under your feet. You are at point A at first and your aim is point B. There are 6 kinds of operations you can perform in one step. That is to go left or right by a,b and c, here c always equals to a+b.
You must arrive B as soon as possible. Please calculate the minimum number of steps.
Input
There are multiple test cases. The first line of input is an integer T(0 < T ≤ 1000) indicates the number of test cases. Then T test cases follow. Each test case is represented by a line containing four integers 4 integers A, B, a and b, separated by spaces. (-231 ≤ A, B < 231, 0 < a, b < 231)
Output
For each test case, output the minimum number of steps. If it's impossible to reach point B, output "-1" instead.
Sample Input
2
0 1 1 2
0 1 2 4
Sample Output
1
-1题意:
你要从一个起点走到一个终点,每一步你有三种走法,走a步,走b步,走a+b步,可以往左也可往右。
可以想象成是一个一维的坐标系,求最小的步数到终点,如果不能到,输出-1。
那么经过一番思考,终于发现,只要解一个方程就行了。
a*x+b*y=c
其中c=B-A,也就是,c为终点和起点的距离
那么解这个方程固然好解,直接套拓展欧几里得模板,但是和最小步数的关系,又有一番推导了。
当时WA的我差点看了题解,不过还好,在绝望之际AC,终于又没看题解完完全全做出一道题。
#include<cstdio>
#include<iostream>
#include<cstdlib>
#include<queue>
#include<cstring>
#include<algorithm>
#include<set>
#include<string>
#include<map>
#include<cmath>
#include<vector>
#include<time.h>
#define fori(l,r) for( int i = l ; i <= r ; i++ )
#define forj(l,r) for( int j = l ; j <= r ; j++ )
#define fork(l,r) for( int k = l ; k <= r ; k++ )
#define mem(a,val) memset(a,val,sizeof a)
#define lef rt<<1
#define rig rt<<1|1
#define mid (l+r)>>1
#define inf 0x3f3f3f3f
#define llinf 0x3f3f3f3f3f3f3f3f
using namespace std;
typedef long long ll;
const int maxn = 1e4+4;
ll x,y;
ll exgcd( ll a,ll b )
{
if( b == 0 )
{
x = 1;
y = 0;
return a; //返回gcd(a,b)
}
ll ans = exgcd(b,a%b);
ll t = x; x = y;
y = t-a/b*y;
return ans;
}
int main()
{
ll A,B,a,b,c,g;
int T;
scanf("%d",&T);
while( T-- )
{
cin>>A>>B>>a>>b;
c = B-A;
g = exgcd(a,b);
if( c%g != 0 )
{
puts("-1");
continue;
}
x = c/g*x,y = c/g*y;
ll t = (y-x)*g/(a+b);
ll ans = llinf;
for( ll i = t-1 ; i <= t+1 ; i++ )
{
ll xx = x+b/g*i;
ll yy = y-a/g*i;
if( xx >= 0 && yy >= 0 )
ans = min(ans,max(xx,yy) );
else if( xx >= 0 && yy < 0 )
ans = min(ans,xx-yy);
else if( xx < 0 && yy >= 0 )
ans = min(ans,yy-xx);
else if( xx < 0 && yy < 0 )
ans = min(ans,max(abs(xx),abs(yy)) );
}
cout<<ans<<endl;
}
return 0;
}
/*
//freopen("E:\\problem list\\codeblocks\\A\\input.txt","r",stdin);
//freopen("E:\\problem list\\codeblocks\\A\\standardoutput.txt","w",stdout);
12312
0 7 1 2
*/