统计学习方法（2）感知机

—— 神经网络与支持向量机(SVM)的基础

从统计学习方法的三要素入手：

感知机学习旨在求出将训练数据进行线性划分的分离超平面，为此，导入基于误分类的损失函数，利用梯度下降法对损失函数进行极小化，求得感知机模型。

感知机对应于输入空间中将实例划分为正负两类的分离超平面，属于判别模型。

1、模型

对于输入空间，通过以下函数将其映射至{+1，-1}的输出空间：
$f(x) = sign(w \cdot x + b)$ 称为感知机，其中 $\omega$ 和 $b$ 为感知机模型参数， $\omega \in \bf R^n$ 叫做权值或权值向量， $b \in \bf R$ 叫做偏置， $\omega·x$ 表示 $\omega$ 和 $b$ 的内积，sign是符号函数。

感知机学习，由训练数据集：
$T = {(x_1, y_1), (x_2, y_2), ..., (x_N, y_N)}$ 其中， $x_i∈\mathcal {X}={\bf R}^N , y_i∈\mathcal {Y}=\{+1, -1\}, \; i=1,2,…,N$ ，求得感知机模型 $f(x) = sign(w \cdot x + b)$ ，即求得模型参数 $\omega$ ， $b$ 。

2、策略

定义损失函数：

假设训练数据集是线性可分的，感知机学习的目标是求得一个能够将训练集正实例点和负实例点完全正确分开的分离超平面。为了找出这样的超平面，即确定感知机模型参数w，b，需要确定一个学习策略，即定义（经验）损失函数并将损失函数极小化。
损失函数的一个自然选择是误分类点的总数。但是，这样的损失函数不是参数w，b的连续可导函数，不易优化。损失函数的另一个选择是误分类点到超平面S的总距离，这是感知机所采用的。

所有误分类的点到超平面S的总距离为：
$-{1\over ||\omega||}\sum_{x_i \in M}y_i(\omega·x_i+b)$
不考虑 $-{1\over ||\omega||}$ ，就得到感知机学习的损失函数。

给定训练数据集： $T = {(x_1, y_1), (x_2, y_2), ..., (x_N, y_N)}$ ，感知机 $sign(\omega·x+b)$ 的损失函数定义为：
$L(w,b) = - \sum\limits_{{x_i} \in M} {{y_i}(w \cdot {x_i} + b)}$
这个损失函数就是感知机学习的经验风险函数。

感知机学习的策略是在假设空间中选取使上面损失函数式最小的模型参数w，b，即感知机模型。

3、算法

感知机学习问题转化为求解损失函数式的最优化问题，最优化的方法是随机梯度下降法。感知机学习的具体算法包括原始形式和对偶形式：

3.1 原始形式

给定一个训练数据集： $T = {(x_1, y_1), (x_2, y_2), ..., (x_N, y_N)}$
其中， $x_i∈\mathcal {X}={\bf R}^N , y_i∈\mathcal {Y}=\{+1, -1\}, \; i=1,2,…,N$ ，求参数 $\omega$ 和 $b$ ，使其为以下损失函数极小化问题的解：
$\min_{\omega,b}L(w,b) = - \sum\limits_{{x_i} \in M} {{y_i}(w \cdot {x_i} + b)}$
极小化过程采用随机梯度下降法：
损失函数 $L(\omega, b)$ 的梯度为：
$\nabla_\omega L(\omega, b)=-\sum_{x_i\in M}y_ix_i\\ \nabla_b L(\omega, b)=-\sum_{x_i\in M}y_i$
随机选取一个误分类点 $(x_i, y_i)$ ，对 $\omega, b$ 进行更新：
$\omega \leftarrow \omega+\eta y_ix_i\\ b \leftarrow b+\eta y_i$
所以，整个算法流程如下：
（1）选取初值 $\omega_0, b_0$ ;
（2）在训练集中任意选取点 $(x_i, y_i)$ ;
（3）如果 $−y_i(\omega⋅x_i+b)>0$ 则按照(4)式更新 $w, b$ ;
（4）重复（2）直到没有被误分的点。

一个实例：
在这里插入图片描述

3.2 对偶形式

对偶形式的基本想法是，将 $\omega$ 和b表示为实例x，和标记y的线性组合的形式，通过求解其系数而求得 $\omega$ 和b。

感知机学习算法的原始形式和对偶形式与支持向量机学习算法的原始形式和对偶形式相对应。

假设 $\omega_0=0, b=0$ ，对于训练集中的N个点，当所有的点均不发生误判时，最后学习到的 $\omega, b$ 一定有如下的形式:
$w = \sum\limits_{i = 1}^N {{n_i}\eta {y_i}{x_i}} = \sum\limits_{i = 1}^N {{\alpha _i}} {y_i}{x_i}\\ b = \sum\limits_{i = 1}^N {{n_i}\eta {y_i}} = \sum\limits_{i = 1}^N {{\alpha _i}} {y_i}$
其中 $\alpha_i=n_i\eta$ 中 $n_i$ 代表对第i个样本点的学习次数。

实例点更新次数越多，意味着它距离分离超平面越近，也就越难正确分类。换句话说，这样的实例对学习结果影响最大。

这样的实例很有可能就是SVM中的支持向量。

对偶形式的感知机模型如下：
$f(x) = sign(\sum\limits_{j = 1}^N {{\alpha _j}} {y_j}{x_j} \cdot x + b)$

所以，整个算法流程如下：
（1）初始化 $\alpha=0, b=0$
（2）任意选取 $(x_i,y_i)$
（3）如果 $y_i(\sum\limits_{j = 1}^N {{\alpha _j}} {y_j}{x_j} \cdot x_i + b)\le0$ ，即发生误判，则对 $\alpha_i,b$ 进行更新：
$\alpha_i\leftarrow \alpha_i+\eta\\ b_i\leftarrow b_i+\eta y_i$ （4）重复（2）直到所有点都被正确分类

一个实例：
在这里插入图片描述

注：

与原始形式相比，对偶形式误分条件的计算反而更复杂，采用Gram矩阵存储实例间的内积计算，提高运算速度；

感知机的对偶形式就是把对 $\omega, b$ 的学习变成了对 $\alpha, b$ 的学习。原始形式中， $\omega$ 在每一轮迭代错分时都需要更新，对偶形式的一个好处是不用每次都更新 $\omega$ ，每次只更新错分点对应的 $\alpha_i$ ，只在最后计算一次 $\omega$ ；

如果只考虑支持向量，则对偶形式误分条件只需要计算支持向量，而不需要计算所有的样本点，须与SVM作对比。

4、实现

4.1 原始形式

import random
import numpy as np
import matplotlib.pyplot as plt

"""
感知机：原始形式
"""

class Perceptron:
    def train(self, train_data, train_num, eta):
        data = np.array(train_data)
        x_len = len(data[0]) - 1
        w = [0.0] * x_len
        b = 0.0
        for i in range(train_num):
            data_row = random.choice(data)
            x = data_row[0:-1]
            y = data_row[-1]
            if y * (np.matmul(w, x.T) + b) <= 0:
                w += eta * y * x
                b += eta * y
        return w, b

    def plot_points(self, train_data, w, b):
        plt.figure()
        x1 = np.linspace(0, 8, 100)
        x2 = (-b-w[0]*x1) / (w[1] + 1e-10)
        plt.plot(x1, x2, color='r', label='y1 data')
        data_len = len(train_data)
        for i in range(data_len):
            if train_data[i][-1] == 1:
                plt.scatter(train_data[i][0], train_data[i][1], s=50, c='black')
            else:
                plt.scatter(train_data[i][0], train_data[i][1], marker='x', s=50, c='black')
        plt.show()


if __name__ == '__main__':
    train_data1 = [[1, 3, 1], [2, 2, 1], [3, 8, 1], [2, 6, 1]]  # 正样本
    train_data2 = [[2, 1, -1], [4, 1, -1], [6, 2, -1], [7, 3, -1]]  # 负样本
    train_datas = train_data1 + train_data2  # 样本集
    P = Perceptron()
    w, b = P.train(train_data=train_datas, train_num=80, eta=0.01)
    print(w, b)
    P.plot_points(train_data=train_datas, w=w, b=b)

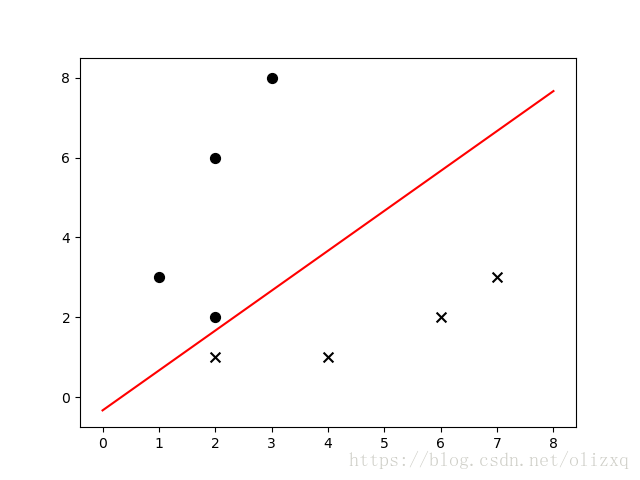
运行结果：

[-0.04  0.05] 0.0

在这里插入图片描述

4.2 对偶形式

import random
import numpy as np
import matplotlib.pyplot as plt

"""
感知机：对偶形式
"""

class Perceptron:
    def train(self, train_data, train_num, eta):
        w = 0.0
        b = 0
        data_len = len(train_data)
        alpha = [0]*data_len
        train_array = np.array(train_data)
        gram = np.matmul(train_array[:, 0:-1], train_array[:, 0:-1].T)
        for idx in range(train_num):
            tmp = 0
            i = random.randint(0, data_len-1)
            yi = train_array[i, -1]
            for j in range(data_len):
                tmp += alpha[j] * train_array[j, -1] * gram[i, j]
            tmp += b
            if yi * tmp <= 0:
                alpha[i] += eta
                b += eta * yi
        for i in range(data_len):
            w += alpha[i]*train_array[i, 0:-1]*train_array[i, -1]
        return w, b

    def plot_points(self, train_data, w, b):
        plt.figure()
        x1 = np.linspace(0, 8, 100)
        x2 = (-b-w[0]*x1) / (w[1] + 1e-10)
        plt.plot(x1, x2, color='r', label='y1 data')
        data_len = len(train_data)
        for i in range(data_len):
            if train_data[i][-1] == 1:
                plt.scatter(train_data[i][0], train_data[i][1], s=50, c='black')
            else:
                plt.scatter(train_data[i][0], train_data[i][1], marker='x', s=50, c='black')
        plt.show()


if __name__ == '__main__':
    train_data1 = [[1, 3, 1], [2, 2, 1], [3, 8, 1], [2, 6, 1]]  # 正样本
    train_data2 = [[2, 1, -1], [4, 1, -1], [6, 2, -1], [7, 3, -1]]  # 负样本
    train_datas = train_data1 + train_data2  # 样本集
    P = Perceptron()
    w, b = P.train(train_data=train_datas, train_num=500, eta=0.01)
    print(w, b)
    P.plot_points(train_data=train_datas, w=w, b=b)

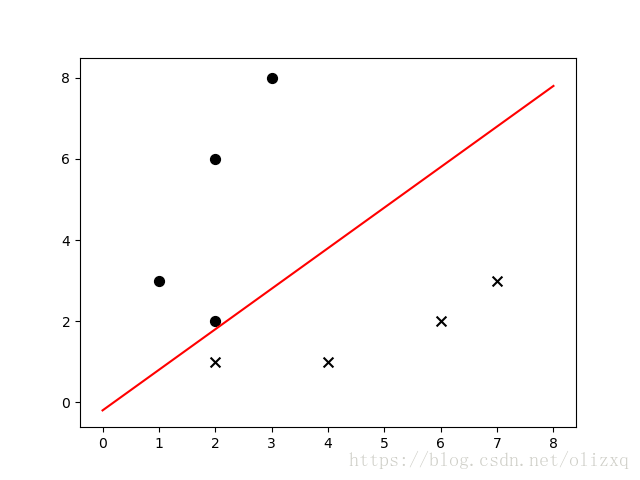
运行结果：

[-0.05  0.05] 0.01

在这里插入图片描述

参考：
《统计学习方法》李航
https://blog.csdn.net/winter_evening/article/details/70196040