递归的基本概念:一个函数调用其本身。
经典递归程序,求N的阶乘:
int Factorial(int n)
{
if(n == 0)
return 1;
return n*Factorial(n-1);
}这个递归程序的时间复杂度为O(n)。
递归和普通函数一样都是通过栈来实现的。
递归的作用 :
1) 替代多重循环
2) 解决本来就是用递归形式定义的问题
3) 将问题分解为规模更小的子问题进行求解
递归经典习题:
1.汉诺塔问题:
汉诺塔(Hanoi Tower),又称河内塔,源于印度一个古老传说。大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,任何时候,在小圆盘上都不能放大圆盘,且在三根柱子之间一次只能移动一个圆盘。问应该如何操作?
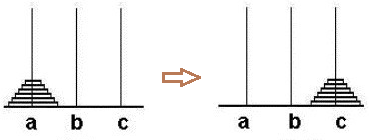
一股脑地考虑每一步如何移动很困难,我们可以换个思路。先假设除最下面的盘子之外,我们已经成功地将上面的63个盘子移到了b柱,此时只要将最下面的盘子由a移动到c即可。如图:

当最大的盘子由a移到c后,b上是余下的63个盘子,a为空。因此现在的目标就变成了将这63个盘子由b移到c。这个问题和原来的问题完全一样,只是由a柱换为了b柱,规模由64变为了63。因此可以采用相同的方法,先将上面的62个盘子由b移到a,再将最下面的盘子移到c……对照下面的过程,试着是否能找到规律:
- 将b柱子作为辅助,把a上的63个圆盘移动到b上
- 将a上最后一个圆盘移动到c
- 将a作为辅助,把b上的62个圆盘移动到a上
- 将b上的最后一个圆盘移动到c
- ......
也许你已经发现规律了,即每次都是先将其他圆盘移动到辅助柱子上,并将最底下的圆盘移到c柱子上,然后再把原先的柱子作为辅助柱子,并重复此过程。
程序实现(C++):
#include <iostream>
using namespace std;
void Hanoi(int n, char src, char mid, char dest, int src_n)
//将src柱子上的n个盘子以mid为中转,移动到dest柱上
//src柱子上最上册的盘子编号是src_n
{
if(n == 1)//只需移动一个盘子
{
cout<<src_n<<": "<<src<<"->"<<dest<<endl;//直接将盘子从src移动到dest即可
return ;
}
Hanoi(n-1, src, dest, mid, src_n);//先将n-1个盘子从src移动到mid
cout<<src_n+n-1<<": "<<src<<"->"<<dest<<endl;
//再将一个盘子从src移动到dest
Hanoi(n-1, mid, src, dest, src_n);//最后再将n-1个盘子从mid移动到dest
}
int main()
{
char src,mid,dest;
int n;
cin>>n>>src>>mid>>dest;
Hanoi(n, src, mid, dest, 1);
return 0;
}
2.用递归替代多重循环
N皇后问题:
输入整数n, 要求n个国际象棋的皇后,摆在n*n的棋盘上,互相不能攻击,输出全部方案。(注:根据国际象棋规则,当两个皇后在同一行同一列或同一对角线上时,则可以互相攻击)。
输入一个正整数N,则程序输出N皇后问题的全部摆法。输出结果里的每一行都代表一种摆法。行里的第i个数字如果是n,就代表第i行的皇后应该放在第n列。皇后的行、列编号都是从1开始算。
样例输入:
4
样例输出:
2 4 1 3
3 1 4 2
解法思路:
该题很容易想到循环求解,但是N是未知的?N重循环。一个很容易理解的递归思路是,假设前K位已经排好了,来摆第K个皇后的位置,只要保证不与前面的冲突即可,然后递归摆K+1个皇后的位置。
程序实现(C++):
#include <iostream>
#include <cmath>
using namespace std;
int N;
int queenPos[100];
//用来存放算好的皇后位置。最左上角是(0,0)
void NQueen(int k);
int main()
{
cin>>N;
NQueen(0); //从第0行开始摆皇后
return 0;
}
void NQueen(int k) //在0~k-1行皇后已经摆好的情况下,摆第k行及其后的皇后
{
int i;
if(k==N) // N 个皇后已经摆好
{
for(i=0;i<N;i++)
cout<<queenPos[i]+1<<" ";
cout<<endl;
return ;
}
for(i=0;i<N;i++) //逐尝试第k个皇后的位置
{
int j;
for(j=0;j<k;j++)
{
if(queenPos[j]==i || abs(queenPos[j]-i)==abs(k-j)) //和已经摆好的 k 个皇后的位置比较,看是否冲突
{
break;//冲突,则试下一个位置
}
}
if(j==k) //当前选的位置 i 不冲突
{
queenPos[k]=i; //将第k个皇后摆放在位置 i
NQueen(k+1);
}
}
}
3.用递归解决递归形式的问题:
波兰表达式
波兰表达式是一种把运算符前置的算术表达式,例如普通的表达式2 + 3的逆波兰表示法为+ 2 3。逆波兰表达式的优点是运算符之间不必有优先级关系,也不必用括号改变运算次序,例如(2 + 3) * 4的逆波兰表示法为* + 2 3 4。本题求解逆波兰表达式的值,其中运算符包括+ - * /四个。
输入
输入为一行,其中运算符和运算数之间都用空格分隔,运算数是浮点数
输出
输出为一行,表达式的值。
样例输入
* + 11.0 12.0 + 24.0 35.0
样例输出
1357.000000
提示:(11.0+12.0)*(24.0+35.0)
程序实现(C++):
#include <iostream>
#include <cstdio>
#include <cstdlib>
using namespace std;
double exp()//读入一个逆波兰表达式,并计算其值
{
char s[20];
cin>>s;
switch(s[0])
{
case '+':return exp()+exp();
case '-':return exp()-exp();
case '*':return exp()*exp();
case '/':return exp()/exp();
default: return atof(s);
break;
}
}
int main()
{
printf("%lf",exp());
return 0;
}
这个题还可以使用栈来求解。
课后习题:
1:全排列
总时间限制:
1000ms
内存限制:
65536kB
描述
给定一个由不同的小写字母组成的字符串,输出这个字符串的所有全排列。 我们假设对于小写字母有'a' < 'b' < ... < 'y' < 'z',而且给定的字符串中的字母已经按照从小到大的顺序排列。
输入
输入只有一行,是一个由不同的小写字母组成的字符串,已知字符串的长度在1到6之间。
输出
输出这个字符串的所有排列方式,每行一个排列。要求字母序比较小的排列在前面。字母序如下定义:
已知S = s1s2...sk , T = t1t2...tk,则S < T 等价于,存在p (1 <= p <= k),使得
s1 = t1, s2 = t2, ..., sp - 1 = tp - 1, sp < tp成立。
样例输入
abc
样例输出
abc acb bac bca cab cba
解法思路:
这个题有多种解法,最基本的就是拿到字符串进行一个重排序,保证字符串中的字母已经按照从小到大的顺序排列(本题已假定)。比如对于字符串abc,最小的排列方式就是abc本身,其次是最后两位颠倒acb,接着是a和b互换bca,但明显bca不是第三组排列,存在比它小的还未出现的排列是bac。
经过分析发现存在这种规律:对于一个字符串abcde,当字符串升序排列是达到最小的排列方式;当字符串降序排列时达到最大的排列方式,即edcba。算法首先从头开始找到字符串中生序排列的最后一位字符i,再从尾找到大于它的第一个字符j,两者互换,如果i+1~j的字符串是非升序的,再将互换后i+1~j的字符串再次颠倒,即得到当前排列的下一个排列方式。如abdce,首先找到d,再从尾部找到e,de互换后为abecd,此时已经达到升序,不用颠倒,abecd也的确是abdce的下一个排列。
程序实现(C++) 该代码未AC:
#include <iostream>
#include <string.h>
using namespace std;
void swapc(char &a,char &b)
{
char temp;
temp=a;
a=b;
b=temp;
}
void Permutation(char s[], int k, int m)
{
if(k==m)
{
cout<<s<<endl;
return;
}
else{
for(int i=k;i<=m;i++)
{
swapc(s[k],s[i]);
Permutation(s,k+1,m);
swapc(s[k],s[i]);
}
}
}
int main()
{
char s[20];
cin>>s;
int len=strlen(s);
Permutation(s,0,len-1);
return 0;
}程序实现(C++) 该代码AC:
#include<iostream>
#include<stdio.h>
#include<queue>
#include<string>
#include<string.h>
#include<algorithm>
using namespace std;
char a[10];
int main()
{
int n;
while(scanf("%s",a)!=EOF)
{
n=strlen(a);
do
{
printf("%s\n",a);
}while(next_permutation(a,a+n));
puts("");
}
return 0;
}C++提供的next_permutation(start,end),和prev_permutation(start,end)。这两个函数作用是一样的,区别就在于前者求的是当前排列的下一个排列,后一个求的是当前排列的上一个排列。至于这里的“前一个”和“后一个”,我们可以把它理解为序列的字典序的前后,严格来讲,就是对于当前序列pn,他的下一个序列pn+1满足:不存在另外的序列pm,使pn<pm<pn+1.
因此如果提前将数组排好序,那么next_permutation(start,end)会求得该数组的全排列。
2:2的幂次方表示
总时间限制:
1000ms
内存限制:
65536kB
描述
任何一个正整数都可以用2的幂次方表示。例如:
137=27+23+20
同时约定方次用括号来表示,即ab可表示为a(b)。由此可知,137可表示为:
2(7)+2(3)+2(0)
进一步:7=22+2+20(21用2表示)
3=2+20
所以最后137可表示为:
2(2(2)+2+2(0))+2(2+2(0))+2(0)
又如:
1315=210+28+25+2+1
所以1315最后可表示为:
2(2(2+2(0))+2)+2(2(2+2(0)))+2(2(2)+2(0))+2+2(0)
输入
一个正整数n(n≤20000)。
输出
一行,符合约定的n的0,2表示(在表示中不能有空格)。
样例输入
137
样例输出
2(2(2)+2+2(0))+2(2+2(0))+2(0)
来源
NOIP1998复赛 普及组 第一题
程序实现(C++) 该代码AC:
#include <iostream>
#include <cmath>
using namespace std;
void compute(int n)
{
if(n > 4)
{
int i=1;
while(pow(2, i) <= n) i++;
cout<<"2(";
compute(i-1);
cout<<")";
if(n-pow(2, i-1))
{
cout<<"+";
compute(n-pow(2, i-1));
}
}
else
{
switch(n)
{
case 1:cout<<"2(0)";break;
case 2:cout<<"2";break;
case 3:cout<<"2+2(0)";break;
case 4:cout<<"2(2)";break;
}
}
}
int main()
{
int n;
cin>>n;
compute(n);
return 0;
}