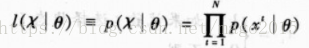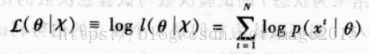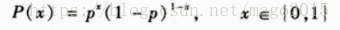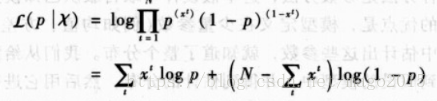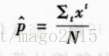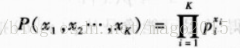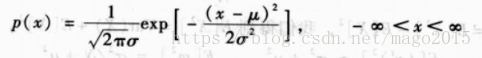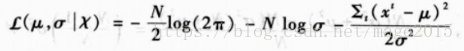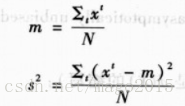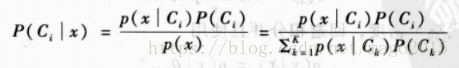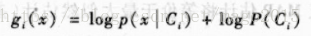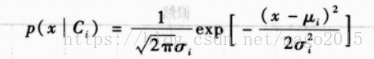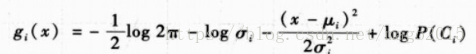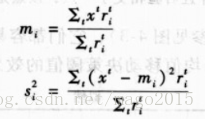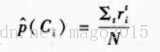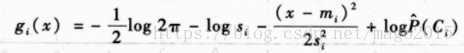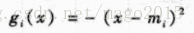前面,我们讨论了贝叶斯方法,使用概率对不确定性建模做出最优决策。现在我们考虑如何从给定的训练集估计这些概率。
引言
参数化方法是指我们假设样本取自服从某种一直模型的某个分布。我们利用最大似然和样本数据近似的估计这个分布的参数信息,从而得出这个分布的一般模型。换言之,一旦从样本中估计出这些参数 ,就知道了整个分布,然后使用它进行决策。
一、最大似然估计
最大似然估计的假设前提,独立同分布样本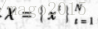
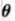
我们希望找出这样的参数,使得样本尽可能像是从
我们感兴趣的是找到这样的参数,使得X最像是从
上述内容详细讲解了,参数估计方法最大似然法。然而,我们对估计的参数的具体形式,还不太清楚。所以针对这个问题,我们引出其他内容。下面内容是介绍当假设我们的类似然函数服从某种分布,我们通过最大似然法求得分布中参数,从而进行决策。
二、常见类似然分布
这里我们以伯努利分布、多项式分布、高斯分布为例。并且以下我们都假设给定样本服从独立同分布。
1、伯努利密度
伯努利分布也叫两点分布或零一分布。白女里随机变量X发生概率为p取值1,时间不发生概率为1-p取值0。其概率密度函数如下:
对应的对数似然函数为:
最大化上述似然函数,求 偏导数 可得到该对数似然的估计 。
.
p的估计是时间发生的次数与实验次数的比值。
2、多项式密度
多项式分布可以看作伯努利分布的推广,其中随机事件的结果不是两种状态,而是K中互斥、穷举状态之一,每种状态出现的概率为pi,其概率密度函数为:
如果xi是0/1,则可以认为它们是K次独立的伯努利试验。
3、高斯密度
高斯分布也叫正太分布,其密度函数为:
对于给定样本
最大似然估计参数为:
三、利用最大似然进行参数化分类
本节将利用前面讲解的贝叶斯规则和最大似然估计方法,解决实际问题中参数化分类方法的公式推导和概念理解。
本节假设作者已了解贝叶斯规则和最大似然方法,具体概念笔者不再一一赘述。直接进行公式推导。
贝叶斯公式:
前面介绍过,贝叶斯公式中的证据项是观测样本的边缘概率,无论正例负例,在同一个样本中,其值固定。所以我们根据贝叶斯公式,得出参数化分类的判别式函数。
或等价于
当我们假设类似然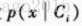
判别式函数变为:
到此,就完成了对参数分类方法的公式推导过程。接下来我们需要求的判别式函数中参数信息,也就是类似然函数所服从的高斯分布的均值和方差信息。因为,我们不能准确知道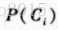
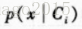
根据样本数据的最大似然估计得到的均值和方差的估计:
最终每个类的判别式的估计为:
有趣的是,第一项是常数,因为它在所有类中都是公共项,如果这些先验也相等,则最后一项也可以去掉,再进一步假设每一个类的方差也相等,则上式变为:
总结:
本节我们使用基于似然的分类方法,其本质是使用数据估计密度,使用贝叶斯计算后验概率,然后得到判别。在以后的我们会讨论基于判别式的分类方法,在哪里我们将直接绕开密度估计直接估计判别式函数来实现分类。对本节内容,简言之,就是为样本数据假设一个概率分布,然后通过最大似然法通过数据求得概率密度函数中的参数信息,进而完成判别式函数的构造。
引:机器学习导论
原创文章,转载注明出处!!!!!