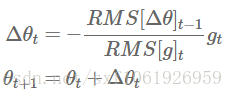总结梯度优化算法

一篇review：https://arxiv.org/abs/1609.04747

三个梯度下降变种：

批梯度下降（Vanilla gradient descent/batch gradient descent）

说白了就是最开始的bp用的东西。它在整个训练数据集上计算梯度
我们需要去计算整个数据集的梯度，然后计算的结果只拿去更新一步梯度，很明显随着数据集变大，批梯度下降会变得很慢而且也会很占内存。批梯度下降也不能用于在线更新模型，即不能实时加新样本。

批梯度下降的伪代码如下

for i in range(epochs):
Params_grad = evaluate_gradient(loss_function,data,params)
Params = params -learning_rate * params_grad

如果对梯度反传还有疑问的可以先看我博客的LR例子理解下梯度反传http://blog.csdn.net/sxf1061926959/article/details/66976356
epochs是事先定义好的，需要迭代的次数。每次迭代批梯度下降都会去计算整个数据集的梯度。

随机梯度下降（Stochastic gradient descent）

大家也看到了批梯度下降的缺点，每次都要在整个数据集上去计算梯度值，一旦数据量较大，可以想象没更新一次得多久。所以就有了随机梯度下降。随机梯度下降刚好和批梯度下降想法，它为了加快计算速度，然后牺牲了准确度，它针对每个样本都去更新一次梯度，就是每计算一个样本的梯度就拿去更新参数。这样的话梯度更新随机性很会大，但是能加快训练速度，而且能在线学习。如下图所示
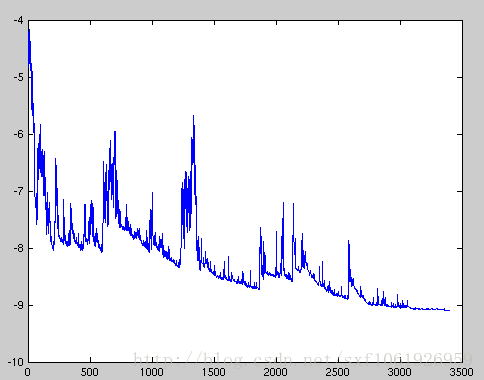
这里写图片描述
网络收敛损失由很大的波动。但是这也不一定是坏事，也是这损失跳来跳去还能跳过局部最小值也说不定呢。具体伪代码如下

for i in range(nb_epochs):
  np.random.shuffle(data)
  for example in data:
    params_grad = evaluate_gradient(loss_function, example, params)
    params = params - learning_rate * params_grad

小批梯度下降（Mini-batch gradient descent）
其实我们现在常说的SGD反而是这种。
前面的两个方法其实都有点极端，所以小批次梯度下降取两者精华。它每次更新参数不计算整个数据集的样本也不计算一个样本，而是随机从样本中选择n个样本。这样也不会像随机梯度下降那样波动的厉害，也能避免批梯度下降速度慢的缺点。伪代码如下：

for i in range(nb_epochs):
  np.random.shuffle(data)
  for batch in get_batches(data, batch_size=50):
    params_grad = evaluate_gradient(loss_function, batch, params)
    params = params - learning_rate * params_grad

其实现在我们习惯说的随机梯度下降大多数指的都是这个，而不是一个样本更新一次的那个，这个需要注意。
上面的三个其实都只是在梯度下降算法输入数据上的变化，并没有改变其基本的算法结构。但是它还是存在一些问题的，比如学习率learning_rate的设置一直是个大问题，大了难以收敛，小了又慢的要死。当然也能实现设定学习率怎么变化，但是也是有局限性的。而且数据并不是一维的，每个维度上的梯度又不一样。

梯度优化算法

momentum

Momentum是在原有的SGD上添加了一个动量
这里写图片描述
像这个图，因为梯度在不同维度上是不同的，而如果用SGD去更新的话，它并不会因为不同维度上梯度的不同而且改变更新的步长，这就导致较为平的维度更新慢。所以这里引入了momentum。

和之前的SGD不同的是，momentum添加了一个变量V，这里定义为速度。这里的mu是一个0到1之间的超参数，一般设置为0.9.
这里方法可以简单理解为，一个球滚动着接近图中的中心（最小值）。我们可以把这里的梯度理解为重力势能，然后在重力势能的作用下一直向下滑动。那么这整个梯度更新的过程便变成，小球在重力势能的作用下向下滚动。理想情况下，小球没有受到其他作用力，就会一直加速向下运动，但是momentum给它加了一个摩擦力，这里摩擦力就是mu*V。它每一次迭代都会在原来的速度上进行减速，因为mu是0到1之间的数。如果没有这里摩擦力，小球永远不会停下来，一直在平面上来回滚，没有能量的损失，那么损失函数很难最小化。加了这个摩擦力后，小球就可以滚啊滚的，慢慢把速度降下来。所以小球在比较平的梯度上，因为速度小，加上梯度方向上的速度，所以整体的速度会变快。但是到比较陡峭的方向上，速度加得比较快，可以理解为V很大，那么摩擦力带来的减速速效果要明显大于梯度方向更新带来的加速。这样的话V的前后两部分公式，来回拉扯，减少了小球在这个方向上的振幅。一般V初始化为0，mu常去0.5到0.9之间的数。
这里写图片描述
用了momentum后的效果如上图

Nesterov accelerated gradient(nag)

一般情况下nag的效果要比momentum的好
这可以算是一个特殊的momentum，看公式就能发现，
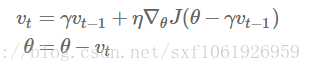
这里写图片描述
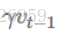
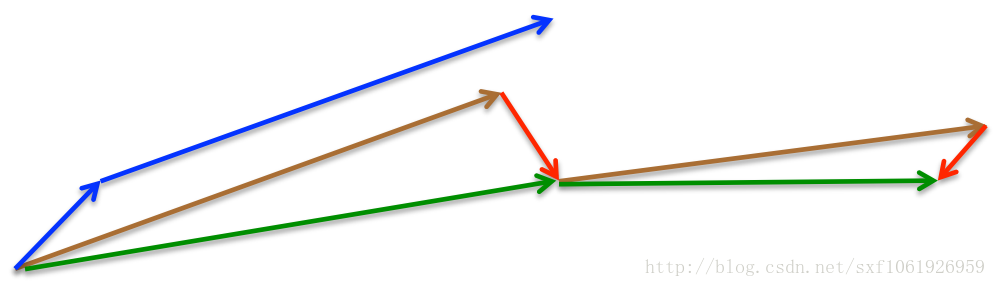
它和momentum的不同是，它提前去计算了下一个位置的梯度，相当于做了一个预测，因为从momentum的那个公式可以发现，它下一步肯定会走到的位置，所以它直接去预测了下一个位置的梯度，下个位子梯度比较陡的话就走大一点，下个位置比较平的话就走慢一点。
这里写图片描述
看图中，棕色的向量就是momentum更新的方向，然后红色的就是去做了一个预测。其实就是事先对梯度进行了修正。

Adagrad

和前面两种改进不同，之前的两种momentum和nesterov momentum是在梯度更新上做修改，Adagrad可以说是在学习率上做了优化。
原始的SGD是这样的

W+=-Learning_rate*dx

现在他尝试根据迭代次数以及梯度来实时调节学习率

Cache+= dx**2
W+=-Learning_rate*dx/(np.sqrt(cache)+1e-8)

这样的话cache是一直越来越大的，使得学习率慢慢变小，一直去调整学习率。而且每个W都会有自己唯一的学习率，去适应自己的scale。Adagrad的最大的好处就是不用再去手动调节学习率，大多数情况下给个默认值0.01然后就不用管了。
例如当垂直方向梯度大，那么cache大，那么np.sqrt(cache)大，learning_rate/np.sqrt(cache)小，相当于有一个小的学习率。
当水平方向梯度平滑，cache小，np.sqrt(cache)小，learning_rate/np.sqrt(cahe)大，相当于有一个大的学习率。
但是也有一个问题，cache一直越来越大，更新步长会逐渐衰减为0，最后就没了。
所以Hiton对Adagrad做了小小的修改。1e-8只是为了防止分母为0。

RMSProp

这里注意，一般cache初始为0.
Adagrad的伪代码：

Cahce += dx**2
W+= -learning_rate*dx/(np.sqrt(cache)+1e-70)

修改为：

Cache = decay_rate*cache+ (1-decay_rate)*dx**2
W+=-learning_rate*dx/(np.sqrt(cache)+1e-7)

通常decay_rate设置较大，如0.99，使得梯度更新方向不变，但不会停止。

AdaDelta

Adadelta是Adagrad的进一步扩展，它和RMSProp是同一时间提出的，两者前面是一样的。相对于Adagrad使用了之前全部的平方梯度，Adadelta限制了所使用的之前梯度的窗口，只使用了前w个梯度。
而且它不是只存储前w个梯度的平方，还定义了一个梯度平方的衰减，具体公式如下
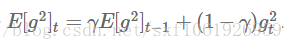
这里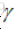写图片描述
这里的有点类似momentum里的超参，通常设置为一个较大的0到1之间的数
然后参数更新就是
可以简写为

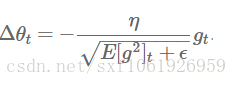
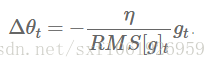
然后作者发现这步更新中单位并不匹配（SGD/momentum/adagrad）都存在这个问题。所以他想去统一下单位。所以他定义了一个参数平方的衰减系数：
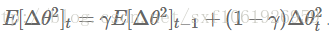
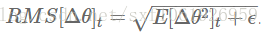
这里写图片描述开平方根后得到

因为这个是未知的，所以用参数的平方误差去近似，再去替换原有的学习率就得到了

Adam（Adaptive moment estimation）

上面的方法都对SGD做了优化，有从梯度优化的，也有从学习率优化的。这个方法可以说是把momentum和adagrad结合了一下。
伪代码如下：

m,v=0
for t in range(0,big_number):
    dx=0
    m=B1*m+(1-B1)*dx
    v=B2*v+(1-B2)*(dx**2)
    m/=1-B1**t
    v/=1-B2**t
    W+=-learning_rate*m/(np.sqrt(v)+1e-7)