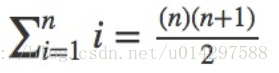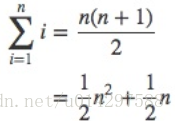目录
1.1.目标
- 理解算法分析的重要性
- 能否使用 大O 符号描述算法的执行时间
- 能够理解Python列表和字典的常见操作的 大O 执行时间
- 能够理解Python数据的实现是如何影响算法分析的
- 了解如何对简单的Python程序做基准测试(benchmark)
1.2.什么是算法分析
一些普遍的现象是刚接触计算机科学的人会将自己的程序和其他人的相比较。你可能还注意到,这些计算机程序看起来很相似,尤其是简单的程序。经常出现一个有序的问题。当两个程序解决同样的问题,看起来不同,哪一个更好呢?
为了回答这个问题,我们需要记住,程序和程序代表底层算法之间有一个重要的区别。一种算法是一个通用的,一步一步解决某种问题的指令列表。它是用于解决一种文体的任何实例的方法,给特定输入,产生期望的结果。另一方面,程序是使用某种编程语言编码的算法。根据程序员和他们所使用的编码语言不听,可能存在描述相同算法的许多不同的程序。
要进一步讨论这种差异,请参考ActiveCode1中显示的函数。这个函数解决了一个我们熟悉的问题,计算前n个整数和。该算法使用初始化值为0的累加器(accumulator)变量。然后迭代n个整数,将每个一次天界到累加器。
ActiveCode1
def sumOfN(n):
theSum = 0
for i in range(1,n+1):
theSum = theSum + i
return theSum
print(sumOfN(10))
现在看看ActiveCode2中的函数。刚开始看,它可能很奇怪,但进一步的观察,你可以看到这个函数本质上和前一个函数在做同样的事情。不直观的原因在于编码习惯不好。我们没有使用良好的标识符(identifier)名称来提升可读性,我们在迭步骤中使用了一个额外的天赋语句,这病不是真正必要的。
ActiveCode2
def foo(tom):
fred = 0
for bill in range(1,tom+1):
barney = bill
fred = fred + barney
return fred
print(foo(10))哪个函数更好?取决于你的标准。如果你关注可读性,函数sumOfN可定比foo好。事实上,你可能已经在介绍编程的课程中看到很多例子,他们的目标之一就是帮助你编写易于阅读和理解的程序。然而,在本课程中,我们对算法本事的表示更感兴趣。
算法分析是基于每种算法使用的计算资源量来比较算法。我们比较两个算法,说一个比另一个算法好的原因在于它在使用资源方面更有效率,或者仅仅使用的资源更少。从这个角度看,上面两个函数看起来很相似。它们都是用基本相同的算法来解决求和问题。
在这点上重要的是更多地考虑我们真正意义上的计算资源。有两种方法,一种是考虑算法解决问题所需的空间或者内存。解决方案所需的空间通常由问题本身决定。但是,有时候有的算法会有一些特殊的空间需求,这种情况下我们非常仔细地解释这些变动。
作为空间需求的一种替代方法,我们可以基于算法执行所需的时间来分析比较算法。这种测量凡是有时被称为算法的“执行时间”或“运行时间”。我们可以通过基准分析(benchmar analysis)来测量函数SumOfN的实行时间。这意味正我们将记录程序计算出结果所需的实际时间。在Python中,我们可以通过记录相对于系统的开始时间和结束时间来对函数进行基准测试。在time模块中有一个time函数,它可以在任意被调用的地方返回系统时钟的当前时间(以秒为单位)。通过在开始和结束的时候分别调用两次time函数,然后计算差异,就可以得到一个函数执行花费的精确秒数(大多数情况下是这样)。
Listing 1
import time
def sumOfN2(n):
start = time.time()
theSum = 0
for i in range(1,n+1):
theSum = theSum + i
end = time.time()
return theSum end-startListing 1 嵌入了时间函数,函数返回一个包含了执行结果和执行消耗时间的元组( tuple )。如果我们执行这个函数 5 次,每次计算前 10,000 个整数的和,将得到如下结果:
>>>for i in range(5):
print("Sum is %d required %10.7f seconds"%sumOfN(10000))
Sum is 50005000 required 0.0018950 seconds
Sum is 50005000 required 0.0018620 seconds
Sum is 50005000 required 0.0019171 seconds
Sum is 50005000 required 0.0019162 seconds
Sum is 50005000 required 0.0019360 seconds我们发现时间是相当一致的,执行这段代码平均需要0.0019秒。如果我们运行计算前
100 000 个整数的和的函数呢?
>>>for i in range(5):
print("Sum is %d required %10.7f seconds"%sumOfN(100000))
Sum is 5000050000 required 0.0199420 seconds
Sum is 5000050000 required 0.0180972 seconds
Sum is 5000050000 required 0.0194821 seconds
Sum is 5000050000 required 0.0178988 seconds
Sum is 5000050000 required 0.0188949 seconds再次的,尽管时间更长,但每次运行所需的时间也是非常一致的,平均大约多10倍。 对于 n等于 1,000,000,我们得到:
>>>for i in range(5):
print("Sum is %d required %10.7f seconds"%sumOfN(1000000))
Sum is 500000500000 required 0.1948988 seconds
Sum is 500000500000 required 0.1850290 seconds
Sum is 500000500000 required 0.1809771 seconds
Sum is 500000500000 required 0.1729250 seconds
Sum is 500000500000 required 0.1646299 seconds在这种情况下,平均值也大约是前一次的10倍。现在考虑 ActiveCode 3,它显示了求解求和问题的不同方法。函数 sumOfN3 利用封闭方程而不是迭代来计算前n个整数的和。
ActiveCode 3
def sumOfN3(n):
return (n*(n+1))/2
print(sumOfN3(10))
如果我们对 sumOfN3 做同样的基准测试,使用 5 个不同的 n (10,000, 100,000, 1,000,000, 10,000,000 和 100,000,000) , 我们得到如下结果
Sum is 50005000 required 0.00000095 seconds
Sum is 5000050000 required 0.00000191 seconds
Sum is 500000500000 required 0.00000095 seconds
Sum is 50000005000000 required 0.00000095 seconds
Sum is 5000000050000000 required 0.00000119 seconds在这个输出中有两件事需要重点关注,首先上面记录的执行时间比之前任何例子都短,另外他们的执行时间和 n 无关,看起来 sumOfN3 几乎不受 n 的影响。
但是这个基准测试能告诉我们什么?我们可以很直观地看到使用了迭代的解决方案需要做更多的工作,因为一些程序步骤被重复执行。这可能是它需要更长时间的原因。此外,迭代方案执行所需时间随着 n 递增。另外还有个问题,如果我们在不同计算机上或者使用不用的编程语言运行这个函数,我们也可能得到不同的结果。如果使用老旧的计算机,可能需要更长时间才能执行完 sumOfN3。
我们需要一个更好的方法来描述这些算法的执行时间。基准测试计算的是程序执行的实际时间。它并不真正地提供给我们一个有用的度量( measurement ),因为它取决于特定的机器,程序,时间,编译器和编程语言。 相反,我们希望有一个独立于所使用的程序或计算机的度量。这个度量将有助于独立地判断算法,并且可以用于比较不同实现方法的算法的效率。
1.3.大O符号
当我们试图通过执行时间来表征算法的效率时,并且独立于任何特定程序或计算机,重要的是量化算法需要的操作或者步骤的数量。选择适当的基本计算单位是个复杂的问题,并且将取决于如何实现算法。对于先前的求和算法,一个比较好的基本计算单位是对执行语句进行计数。在 sumOfN 中,赋值语句的计数为 1 (theSum = 0) ,加上 n 的值(我们执行theSum=theSum+i 的次数)。我们通过函数 T 表示 T(n)=1 + n 。参数 n 通常称为‘问题的规模’,我们称作 ‘T(n) 是解决问题大小为 n 所花费的时间,即 1+n 步长’。在上面的求和函数中,使用 n 来表示问题大小是有意义的。我们可以说,100000个整数和比 1000个问题规模大。因此,所需时间也更长。我们的目标是表示出算法的执行时间是如何相对问题规模大小而改变的。
计算机科学家更喜欢将这种分析技术进一步扩展。事实证明,操作步骤数量不如确定 T(n) 最主要的部分来的重要。换句话说,当问题规模变大时,T(n) 函数某些部分的分量会超过其他部分。函数的数量级表示了随着 n 的值增加而增加最快的那些部分。数量级通常称为大O符号,写为 O(f(n)) 。它表示对计算中的实际步数的近似。函数 f(n) 提供了 T(n) 最主要部分的表示方法。
在上述示例中, T(n)=1+n 。当 n 变大时,常数 1 对于最终结果变得越来越不重要。如果我们找的是 T(n) 的近似值,我们可以删除 1, 运行时间是 O(n)。要注意,1 对于 T(n) 肯定是重要的。但是当 n 变大时,如果没有它,我们的近似也是准确的。
另外一个示例,假设对于一些算法,确定的步数是 T(n)=5n^2 +27n+1005 。当 n 很小时, 例如1 或 2 ,常数 1005 似乎是函数的主要部分。然而,随着 n 变大,n^2 这项变得越来越重要。事实上,当 n 真的很大时,其他两项在它们确定最终结果中所起的作用变得不重要。当 n 变大时,为了近似 T(n),我们可以忽略其他项,只关注 5n^2 。系数 5 也变得不重要。我们说,T(n) 具有的数量级为 f(n)=n^2。 或者 O( n^2 ) 。
虽然我们没有在求和示例中看到这一点,但有时算法的性能取决于数据的确切值,而不是问题规模的大小。对于这种类型的算法,我们需要根据最佳情况,最坏情况或平均情况来表征它们的性能。最坏情况是指算法性能特别差的特定数据集。而相同的算法不同数据集可能具有非常好的性能。大多数情况下,算法执行效率处在两个极端之间(平均情况)。对于计算机科学家而言,重要的是了解这些区别,使它们不被某一个特定的情况误导。
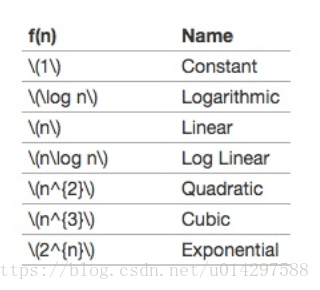
当你学习算法时,一些常见的数量级函数将会反复出现。见 Table 1。为了确定这些函数中哪个是最主要的部分,我们需要看到当 n 变大的时候它们如何相互比较。
Table 1
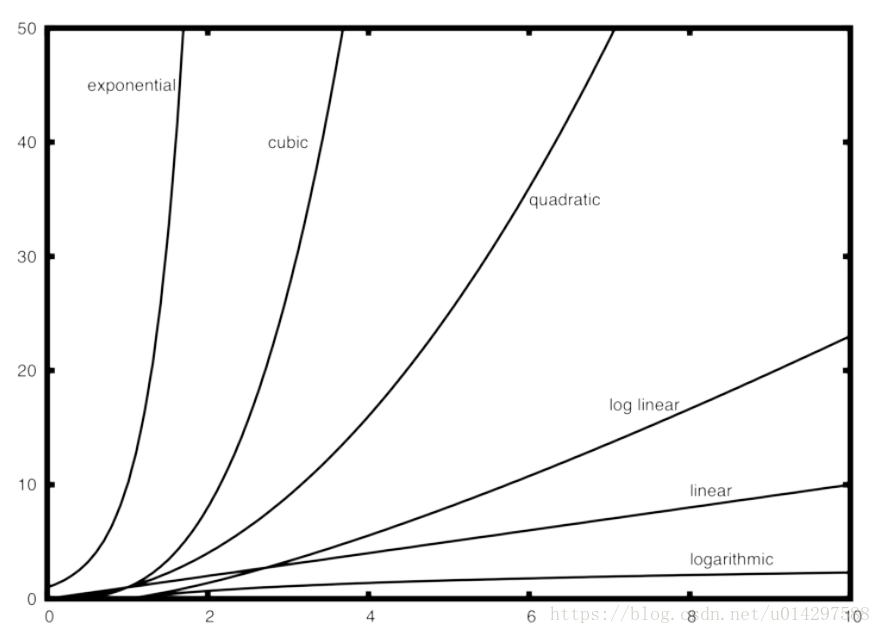
Figure 1 表示了 Table 1 中的函数图。注意,当 n 很小时,函数彼此间不能很好的定义。很难判断哪个是主导的。随着 n 的增长,就有一个很明确的关系,很容易看出它们之间的大小关系。
Figure 1
最后一个例子,假设我们有 Listing2 的代码段。虽然这个程序没有做任何事,但是对我们获取实际的代码和性能分析是有益的。
a=5
b=6
c=10
for i in range(n):
for j in range(n):
x = i * i
y = j * j
z = i * j
for k in range(n):
w = a*k + 45
v = b*b
d = 33Listing 2
分配操作数分为四个项的总和。第一个项是常数 3 ,表示片段开始的三个赋值语句。第二项是3n^2, 因为由于嵌套迭代,有三个语句执行 n^2 次。第三项是 2n,两个语句迭代 n 次。最后,第四项是常数 1,表示最终赋值语句。最后得出 T(n)=3+3n^2 +2n+1=3n^2 + 2n+4,通过查看指数,我们可以看到 n^2 项是显性的,因此这个代码段是 O(n^ 2 )。当 n 增大时,所有其他项以及主项上的系数都可以忽略。
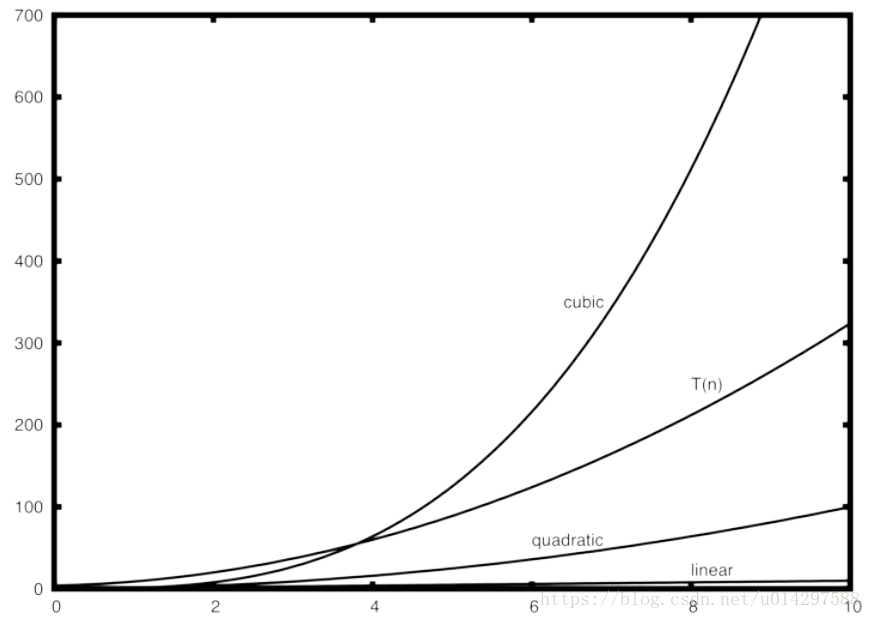
Figure 2
Figure 2 展示了一些常用的 大O 函数,跟上面讨论的 T(n) 函数比较,一开始的时候,T(n) 大于三次函数,后来随着 n 的增长,三次函数超过了 T(n)。T(n) 随着二次函数继续增长。
1.4 一个乱序字符串检查的例子
显示不同量级的算法的一个很好的例子是字符串的乱序检查。乱序字符串是指一个字符串只是另一个字符串的重新排列。例如,'heart' 和 'earth' 就是乱序字符串。'python' 和 'typhon' 也是。为了简单起见,我们假设所讨论的两个字符串具有相等的长度,并且他们由 26 个小写字母集合组成。我们的目标是写一个布尔函数,它将两个字符串做参数并返回它们是不是乱序。
1.4.1.解法1:检查
我们对乱序问题的第一个解法是检查第一个字符串是不是出现在第二个字符串中。如果可以检验到每一个字符,那这两个字符串一定是乱序。可以通过用 None 替换字符来了解一个字符是否完成检查。但是,由于 Python 字符串是不可变的,所以第一步是将第二个字符串转换为列表。检查第一个字符串中的每个字符是否存在于第二个列表中,如果存在,替换成None。见 ActiveCode1
def anagramSolution1(s1,s2):
alist = list(s2)
pos1 = 0
stillOK = True
while pos1 < len(s1) and stillOK:
pos2 = 0
found = False
while pos2 < len(alist) and not found:
if s1[pos1] == alist[pos2]:
found = True
else:
pos2 = pos2 + 1
if found:
alist[pos2] = None
else:
stillOK = False
pos1 = pos1 + 1
return stillOK
print(anagramSolution1('abcd','dcba'))ActiveCode1
为了分析这个算法,我们注意到 s1 的每个字符都会在 s2 中进行最多 n 个字符的迭代。s2 列表中的 n 个位置将被访问一次来匹配来自 s1 的字符。访问次数可以写成 1 到 n 整数的和,
可以写成
当 n 变大,n^2 这项占据主导,1/2 可以忽略。所以这个算法复杂度为 O(n^2 )。
1.4.2.解法2:排序和比较
另一个解决方案是利用这么一个事实:即使 s1,s2 不同,它们都是由完全相同的字符组成的。所以,我们按照字母顺序从 a 到 z 排列每个字符串,如果两个字符串相同,那这两个字符串就是乱序字符串。见 ActiveCode2。
def anagramSolution2(s1,s2):
alist1 = list(s1)
alist2 = list(s2)
alist1.sort()
alist2.sort()
pos = 0
matches = True
while pos < len(s1) and matches:
if alist1[pos]==alist2[pos]:
pos = pos + 1
else:
matches = False
return matches
print(anagramSolution2('abcde','edcba'))ActiveCode2
首先你可能认为这个算法是 O(n),因为只有一个简单的迭代来比较排序后的 n 个字符。但是,调用 Python 排序不是没有成本。正如我们将在后面的章节中看到的,排序通常是O(n^2) 或 O(nlogn)。所以排序操作比迭代花费更多。最后该算法跟排序过程有同样的量级。
1.4.3.解法3: 穷举法
解决这类问题的强力方法是穷举所有可能性。对于乱序检测,我们可以生成 s1 的所有乱序字符串列表,然后查看是不是有 s2。这种方法有一点困难。当 s1 生成所有可能的字符串时,第一个位置有 n 种可能,第二个位置有 n-1 种,第三个位置有 n-3 种,等等。总数为 n∗(n −1)∗(n−2)∗...∗3∗2∗1n∗(n−1)∗(n−2)∗...∗3∗2∗1, 即 n!。虽然一些字符串可能是重复的,程序也不可能提前知道这样,所以他仍然会生成 n! 个字符串。
事实证明,n! 比 n^2 增长还快,事实上,如果 s1 有 20个字符长,则将有 20! =2 432 902 008 176 640 000 个字符串产生。如果我们每秒处理一种可能字符串,那么需要77 146 816 596 年才能过完整个列表。所以这不是很好的解决方案。
1.4.4.解法4: 计数和比较
我们最终的解决方法是利用两个乱序字符串具有相同数目的 a, b, c 等字符的事实。我们首先计算的是每个字母出现的次数。由于有 26 个可能的字符,我们就用 一个长度为 26 的列表,每个可能的字符占一个位置。每次看到一个特定的字符,就增加该位置的计数器。最后如果两个列表的计数器一样,则字符串为乱序字符串。见 ActiveCode 3
def anagramSolution4(s1,s2):
c1 = [0]*26
c2 = [0]*26
for i in range(len(s1)):
pos = ord(s1[i])-ord('a')
c1[pos] = c1[pos] + 1
for i in range(len(s2)):
pos = ord(s2[i])-ord('a')
c2[pos] = c2[pos] + 1
j=0
stillOK = Truewhile j<26 and stillOK:
if c1[j]==c2[j]:
j = j + 1
else:
stillOK = False
return stillOK
print(anagramSolution4('apple','pleap'))ActiveCode 3
同样,这个方案有多个迭代,但是和第一个解法不一样,它不是嵌套的。两个迭代都是 n 第三个迭代,比较两个计数列表,需要 26 步,因为有 26 个字母。一共T(n)=2n+26T(n)=2n+26,即 O(n),我们找到了一个线性量级的算法解决这个问题。在结束这个例子之前,我们来讨论下空间花费,虽然最后一个方案在线性时间执行,但它需要额外的存储来保存两个字符计数列表。换句话说,该算法牺牲了空间以获得时间。很多情况下,你需要在空间和时间之间做出权衡。这种情况下,额外空间不重要,但是如果有数百万个字符,就需要关注下。作为一个计算机科学家,当给定一个特定的算法,将由你决定如何使用计算资源。
1.5.Python数据结构的性能
现在你对 大O 算法和不同函数之间的差异有了了解。本节的目标是告诉你 Python 列表和字典操作的 大O 性能。然后我们将做一些基于时间的实验来说明每个数据结构的花销和使用这些数据结构的好处。重要的是了解这些数据结构的效率,因为它们是本书实现其他数据结构所用到的基础模块。本节中,我们将不会说明为什么是这个性能。在后面的章节中,你将看到列表和字典一些可能的实现,以及性能是如何取决于实现的。
1.6.列表
python 的设计者在实现列表数据结构的时候有很多选择。每一个这种选择都可能影响列表操作的性能。为了帮助他们做出正确的选择,他们查看了最常使用列表数据结构的方式,并且优化了实现,以便使得最常见的操作非常快。当然,他们还试图使较不常见的操作快速,但是当需要做出折衷时,较不常见的操作的性能通常牺牲以支持更常见的操作。
两个常见的操作是索引和分配到索引位置。无论列表有多大,这两个操作都需要相同的时间。当这样的操作和列表的大小无关时,它们是 O(1)。另一个非常常见的编程任务是增加一个列表。有两种方法可以创建更长的列表,可以使用append 方法或拼接运算符。append 方法是 O(1)。 然而,拼接运算符是 O(k),其中 k是要拼接的列表的大小。这对你来说很重要,因为它可以帮助你通过选择合适的工具来提高你自己的程序的效率。让我们看看四种不同的方式,我们可以生成一个从0开始的n个数字的列表。首先,我们将尝试一个 for 循环并通过创建列表,然后我们将使用 append 而不是拼接。接下来,我们使用列表生成器创建列表,最后,也是最明显的方式,通过调用列表构造函数包装 range 函数。
def test1():
l = []
for i in range(1000):
l = l + [i]
def test2():
l = []
for i in range(1000):
l.append(i)
def test3():
l = [i for i in range(1000)]
def test4():
l = list(range(1000))要捕获我们的每个函数执行所需的时间,我们将使用 Python 的 timeit 模块。timeit 模块旨在允许 Python 开发人员通过在一致的环境中运行函数并使用尽可能相似的操作系统的时序机制来进行跨平台时序测量。要使用 timeit,你需要创建一个 Timer 对象,其参数是两个 Python 语句。第一个参数是一个你想要执行时间的 Python 语句; 第二个参数是一个将运行一次以设置测试的语句。然后 timeit模块将计算执行语句所需的时间。默认情况下,timeit 将尝试运行语句一百万次。 当它完成时,它返回时间作为表示总秒数的浮点值。由于它执行语句一百万次,可以读取结果作为执行测试一次的微秒数。你还可以传递 timeit 一个参数名字为 number,允许你指定执行测试语句的次数。以下显示了运行我们的每个测试功能 1000 次需要多长时间。
t1 = Timer("test1()", "from __main__ import test1")
print("concat ",t1.timeit(number=1000), "milliseconds")t2 = Timer("test2()", "from __main__ import test2")
print("append ",t2.timeit(number=1000), "milliseconds")t3 = Timer("test3()", "from __main__ import test3")
print("comprehension ",t3.timeit(number=1000), "milliseconds")t4 = Timer("test4()", "from __main__ import test4")
print("list range ",t4.timeit(number=1000), "milliseconds")
concat 6.54352807999 milliseconds
append 0.306292057037 milliseconds
comprehension 0.147661924362 milliseconds
list range 0.0655000209808 milliseconds在上面的例子中,我们对 test1(), test2() 等的函数调用计时,setup 语句可能看起来很奇怪,所以我们详细说明下。你可能非常熟悉 from ,import 语句,但这通常用在 python 程序文件的开头。在这种情况下, from __main__ import test1 从 __main__ 命名空间导入到 timeit 设置的命名空间中。timeit 这么做是因为它想在一个干净的环境中做测试,而不会因为可能有你创建的任何杂变量,以一种不可预见的方式干扰你函数的性能。
从上面的试验清楚的看出,append 操作比拼接快得多。其他两种方法,列表生成器的速度是append 的两倍。最后一点,你上面看到的时间都是包括实际调用函数的一些开销,但我们可以假设函数调用开销在四种情况下是相同的,所以我们仍然得到的是有意义的比较。因此,拼接字符串操作需要 6.54 毫秒并不准确,而是拼接字符串这个函数需要 6.54 毫秒。你可以测试调用空函数所需要的时间,并从上面的数字中减去它。
现在我们已经看到了如何具体测试性能,见 Table2, 你可能想知道 pop 两个不同的时间。当列表末尾调用 pop 时,它需要 O(1), 但是当在列表中第一个元素或者中间任何地方调用 pop, 它是 O(n)。原因在于 Python 实现列表的方式,当一个项从列表前面取出,列表中的其他元素靠近起始位置移动一个位置。你会看到索引操作为 O(1)。python的实现者会权衡选择一个好的方案。
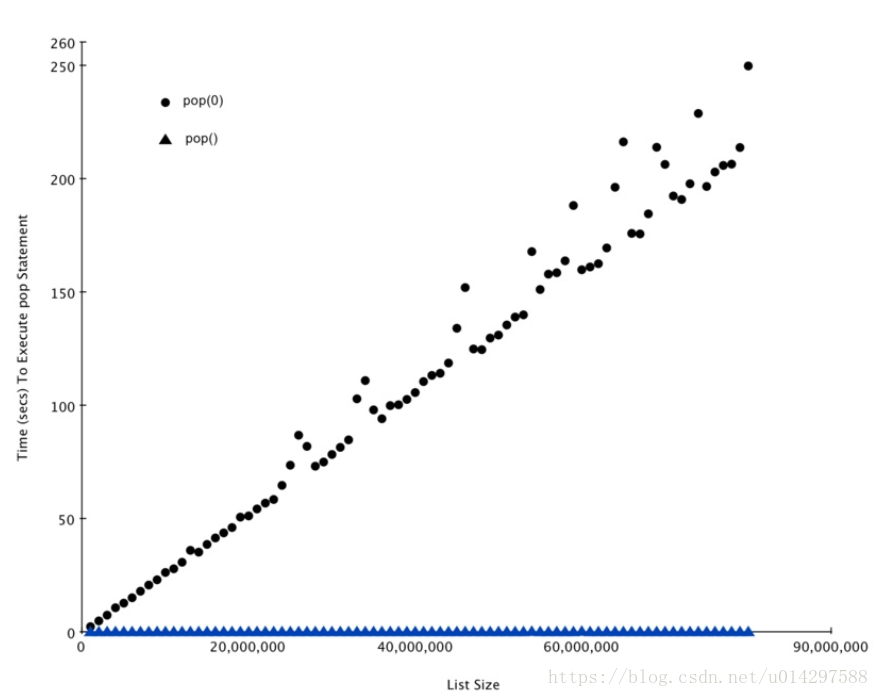
作为一种演示性能差异的方法,我们用 timeit 来做一个实验。我们的目标是验证从列表从末尾 pop 元素和从开始 pop 元素的性能。同样,我们也想测量不同列表大小对这个时间的影响。我们期望看到的是,从列表末尾处弹出所需时间将保持不变,即使列表不断增长。而从列表开始处弹出元素时间将随列表增长而增加。
Listing 4 展示了两种 pop 方式的比较。从第一个示例看出,从末尾弹出需要 0.0003 毫秒。从开始弹出要花费 4.82 毫秒。对于一个 200 万的元素列表,相差 16000 倍。
Listing 4 需要注意的几点,第一, from __main__ import x , 虽然我们没有定义一个函数,我们确实希望能够在我们的测试中使用列表对象 x 这种方法允许我们只计算单个弹出语句,获得该操作最精确的测量时间。因为 timer 重复了 1000 次,该列表每次循环大小都减 1。但是由于初始列表大小为 200万,我们只减少总体大小的 0.05%。
popzero = timeit.Timer("x.pop(0)","from __main__ import x")
popend = timeit.Timer("x.pop()","from __main__ import x")
x = list(range(2000000))
popzero.timeit(number=1000)
4.8213560581207275
x = list(range(2000000))
popend.timeit(number=1000)
0.0003161430358886719 Listing 4
虽然我们第一个测试显示 pop(0) 比 pop() 慢, 但它没有证明 pop(0) 是 O(n), pop()是 O(1)。要验证它,我们需要看下一系列列表大小的调用效果。
popzero = Timer("x.pop(0)","from __main__ import x")
popend = Timer("x.pop()","from __main__import x")
print("pop(0) pop()")
for i in range(1000000,100000001,1000000):
x = list(range(i))
pt = popend.timeit(number=1000)
x = list(range(i))
pz = popzero.timeit(number=1000)
print("%15.5f, %15.5f" %(pz,pt)) Listing 5
Figure 3 展示了我们实验的结果,你可以看到,随着列表变长,pop(0) 时间也增加,而 pop()时间保持非常平坦。这正是我们期望看到的 O(n)和 O(1)。
1.7.字典
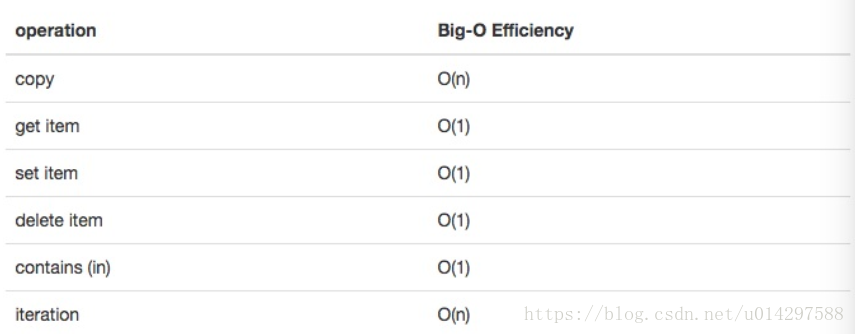
python 中第二个主要的数据结构是字典。你可能记得,字典和列表不同,你可以通过键而不是位置来访问字典中的项目。在本书的后面,你会看到有很多方法来实现字典。字典的 get和 set 操作都是 O(1)。另一个重要的操作是 contains,检查一个键是否在字典中也是 O(1)。所有字典操作的效率总结在 Table3 中。关于字典性能的一个重要方面是,我们在表中提供的效率是针对平均性能。 在一些罕见的情况下,contains,get item 和 set item 操作可以退化为O(n)。我们将在后面的章节介绍。
Table 3
我们会在最后的实验中,将比较列表和字典之间的 contains 操作的性能。在此过程中,我们将确认列表的 contains 操作符是 O(n),字典的 contains 操作符是 O(1)。我们将在实验中列出一系列数字。然后随机选择数字,并检查数字是否在列表中。如果我们的性能表是正确的,列表越大,确定列表中是否包含任意一个数字应该花费的时间越长。
Listing 6 实现了这个比较。注意,我们对容器中的数字执行完全相同的操作。区别在于在第 7行上 x 是一个列表,第9行上的 x 是一个字典。
import timeit
import random
for i in range(10000,1000001,20000):
t = timeit.Timer("random.randrange(%d) in x"%i,"from __main__ import random,x")
x = list(range(i))
lst_time = t.timeit(number=1000)
x = {j:None for j in range(i)}
d_time = t.timeit(number=1000)
print("%d,%10.3f,%10.3f" % (i, lst_time, d_time))Listing 6
Figure 4 展示了 Listing6 的结果。你可以看到字典一直更快。 对于最小的列表大小为10,000个元素,字典是列表的89.4倍。对于最大的列表大小为990,000 个元素。字典是列表的11,603倍!你还可以看到列表上的contains运算符所花费的时间与列表的大小成线性增长。这验证了列表上的contains运算符是 O(n) 的断言。还可以看出,字典中的 contains 运算符的时间是恒定的,即使字典大小不断增长。事实上,对于字典大小为10,000个元素,contains操作占用
0.004毫秒,对于字典大小为990,000个元素,它也占用0.004毫秒。
Figure 4
由于 Python 是一种不断发展的语言,底层总是有变化的。 有关 Python 数据结构性能的最新信息可以在 Python 网站上找到。 在撰写本文时,Python wiki有一个很好的时间复杂性页面,可以在 Time Complexity Wiki 中找到。
2.8 总结
- 算法分析是一种独立的测量算法的方法。
- 大O表示法允许根据问题的大小,通过其主要部分来对算法进行分类。