2006年2月23日晚,在都灵冬奥会自由式滑雪男子空中技巧决赛中,中国选手韩晓鹏以250.77分力挫群雄,以完美的两个动作获得了该项目的金牌,这也是中国在冬奥会上的第一枚自由式滑雪项目金牌。
自由式滑雪空中技巧的分数分为三部分,其中起跳2分,空中动作5分,落地3分,共有5名裁判依次按照这三部分打分。下图是某个运动员在完成一个动作后的分数表:
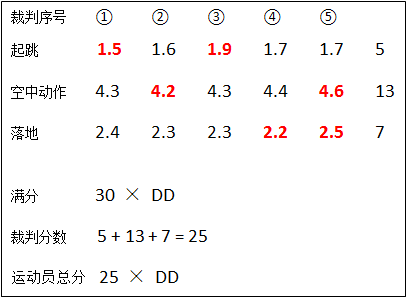
计算裁判分数时,需要将起跳、空中动作、落地三部分中的最高分和最低分去掉(也就是我们经常在比赛中听到的“去掉一个最高分,去掉一个最低分”),剩下的分数相加再乘以该动作的难度系数(Degree of Difficulty,DD)后得到这名运动员本次空中技巧的总分。
为什么需要5位裁判?为什么要去掉最高分和最低分?这需要用一个长长的故事来回答,故事的开头就从误差说起。
误差
误差一词源于测量,是一个量的观测值或计算值与其真实值之间的差异。我们在初中物理中就学过,误差不是错误,误差处处存在。确实如此,比如用直尺测量一本书的厚度,可能得到这样的结果:
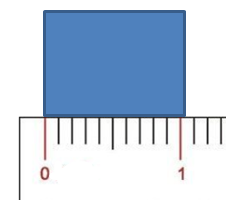
最终结果在1cm和1.1cm之间,究竟是多少?说不清楚,可能恰巧是1.3,也可能是一个无限不循环小数。似乎是刻度不够精确导致了误差,这没错,但工具的精确度只是引起误差的众多原因之一,误差的成因还有很多种。
误差的成因
在测量书的厚度时,工具的精确性造成了误差,除此之外,还有人的因素,你是用什么方法让书的边缘对准零刻度的?不同的人观测也会得到不同的结果,即使同一个人,从不同的角度也可能得到不同的数值。环境因素也会产生误差。同一个物体,在湿度不同的情况下质量会有所差别,也会由于温度的不同而产生热证冷缩,从而导致体积的差异。还有很多时候,误差是人们故意为之,比如常用的“保留小数点后两位数字”。
误差限
误差无处不在且不可避免,但并非不可接受,只要我们将误差控制在合理的范围内即可。怎样才算合理呢?这个要视具体问题而定,比如测量渔政船的长度,少了1米都不可原谅,但是对于测量北京到上海的距离,少个1公里也没那么严重。怎样定义误差限完全取决于自己,只要你觉得范围合理就好。
尽管误差可以接受,但对喜欢追求精确的人们来说仍是个大敌。对于这个消灭不了的敌人,我们的应对策略是尽可能减小误差。
减小误差的方法
如果用ε表示误差,X表示测量值,L表示真实值,那么误差可以这样定义:
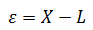
很明显,ε有正有负,ε也被称为绝对误差。
注:除了绝对误差外,还有相对误差、引用误差、标称误差、基值误差等,这里只讨论绝对误差。
我们不讨论如何通过提升仪器精确性和测量方法去减小误差,只讨论数学方案。来看自由式滑雪空中技巧的比赛,对于打分的项目,仅用1个裁判肯定是不靠谱的,再公正的裁判也会不自觉的对自己国家的选手有所偏向,也可能会带有一些个人喜好,所以需要由多个来自不同国家的裁判一起打分。如果运动员的真实分数是L,裁判们的测量值是Xn,那么五个裁判将得到五个误差:

取绝对值是为了让所有误差都是正数,便于接下来的说明。由于误差有正有负,从统计来看,正负各半,所以5个裁判的总误差是:
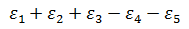
假设所有裁判的误差限都是μ,那么:
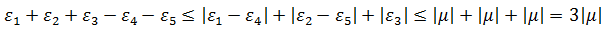
取平均值,每个裁判的误差限变成:

这可比原来的误差限μ小多了。误差限缩小了,误差的波动范围自然也就缩小了,看来增加高水平的裁判人数可以有效减小误差。然而空中技巧的分数表中还去掉了最高分和最低分,按照之前逻辑,裁判的误差限是2|μ|/3,这个结果大于3|μ|/5,为什么要这么做呢?为了弄清楚原因,我们来看另一个例子。
经常有人嘲讽用平均值计算人均GDP的方式:“张家有财一千万,九个邻居穷光蛋,平均一算,家家都是百万”,张千万远远富过邻居们,由于他抬高了平均值,本应该挂上重点扶贫标签的村子变成了反而先进典型。回到自由滑雪,如果把打分最高的裁判看成张千万,就不难理解去掉最高分和最低分的意义。类似的“去掉最高分和最低分”的例子还有很多,比如我们计算国内50寸液晶电视的均价,你不能在把双十一打折时候的价格算进去。
近似
在误差限内的误差是可以接受的,比如北京到上海的航空距离是1213公里,直接省略了小数点后面的数字;国际田联规定,100米的跑道,误差需要控制在+1厘米之内,有很高的精确度……这些类数字都指向一个与误差相关的词——近似。
近似并非依靠经验的估算,计算近似值有一套完整的数学方法,下面就来看看这些神奇的方法。
线性近似
线性近似也叫线性逼近,是最常用的计算近似值的方法,它大概是这么说的,如果小汽车的行驶距离f(t)是关于时间t的函数,假设我们知道小汽车在t0时刻的行驶距离f(t0),那么可以通过t0近似地计算出小汽车在接近t0的时刻t的行驶距离f(t):

线性近似的计算公式来源于导数,把上面的t换成x,根据导数的定义:
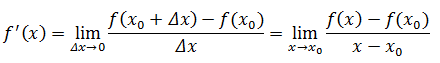
左右两边同时乘以x-x0,并去掉极限符号:

当x≈x0=0时:
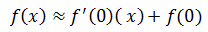
这就是线性近似的公式了,由于计算的是x0附近的近似值,所以x0被称为基点,在讨论近似时,只有指定基点才有意义,也就是指明是在谁附近的近似。线性近似的几何意义是,f(x)在x0的切线近似于原函数的曲线:
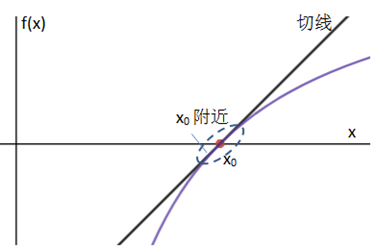
血缘越近,长得越像,在x0点附近,曲线近似于直线,x越接近x0,二者的近似度越高。这很容易理解,x越远离x0,曲线和直线的差距越大;同时,当基点不同时,切线的斜率也不同,所以近似值也不同。下图是(1+x)2在x0 = 0处的近似:
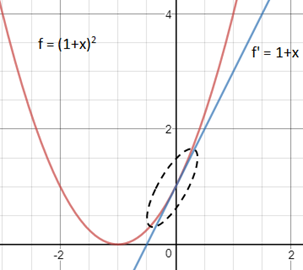
下表是一些常用函数及它们的线性近似:
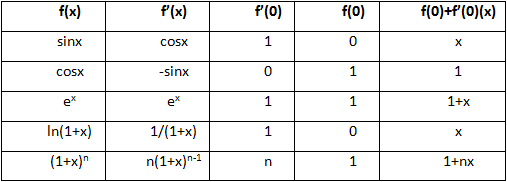
下面通过一个实际例子看看如何使用线性近似。
示例 ln(1.1) ≈ ?
这需要计算器了,现在只需要寻找近似值就可以。
设f(x) = ln(1 + x),当x = 0.1时,ln(1.1) = ln(1 + x)。当x0 = 0,我们认为x = 0.1接近x0,根据表9.7中的线性近似:
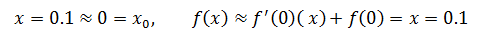
最终求得ln(1.1) ≈ 0.1,通过计算器可算得ln(1.1) ≈ 0.095310179804325,非常接近0.1。至于0.1是否接近于0是个及其主观的判断,要视具体问题而定。某些时候,0.1可能距离0很远,比如在地图上;另一些时候,10也可能距离0很近,比如度量北京到上海的距离。
二阶近似
二阶近似在线性近似的基础上更进一步,把二阶导数也考虑进去,它比一阶近似更为精确,当x≈x0时:
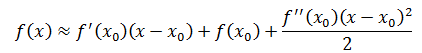
当x≈x0=0时:

二阶近似的几何意义是最接近原函数的抛物线。以f(x) = ln(1 + x)为例:
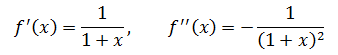
根据公式,在x=x0 = 0处:
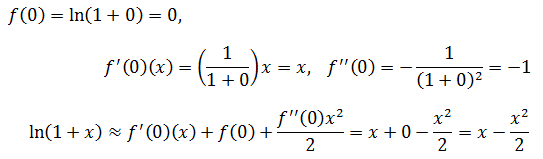

可以用二阶近似计算上一节的例子,设x = 0.1,看看 ln(1.1)在二阶近似下的值:
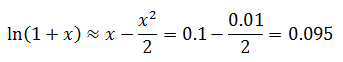
这个结果比一阶近似的值0.1更接近0.095310179804325。
二级近似的几何意义是最接近曲线的抛物线,如果原曲线本身就是抛物线,则二阶近似就是原曲线本身,例如原函是f(x) = a + bx + cx2:
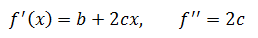
在x = x0 = 0处:
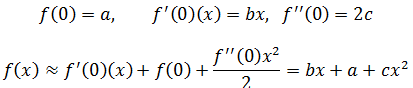
这恰好等于原函数,当然,仅当f(x) = a + bx + cx2时才能如此精确。
下表是一些常用函数及它们的二阶近似:

泰勒公式
泰勒公式是另一种计算近似值的方法,它是一个用函数某点的信息描述在该点附近取值的公式。如果函数足够平滑的话,在已知函数在某一点的各阶导数值的情况之下,泰勒公式可以用这些导数值做系数构建一个多项式来逼近函数在这一点的邻域中的值,如果你愿意,这个多项式可以没完没了。
相比线性近似和二阶近似,泰勒公式要复杂得多,应用也更加广泛。
泰勒级数
如果f(x)在点x = x0具有任意阶导数,那么泰勒公式是这样的:

上式中的幂级数称为f(x)在x0点的泰勒级数。当x0 = 0时,f(x)的泰勒级数是对f进行n次求导之后在零点的值,除以n的阶乘再乘以xn:
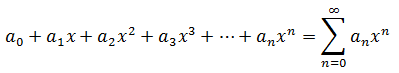
泰勒级数是一种特殊的幂级数,幂级数是这样定义的:

实际上,在泰勒级数我们重新定义了an:

来看看an是怎么得到的。
先设置一个无穷级数f(x):
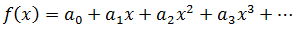
再对f(x)反复求导:
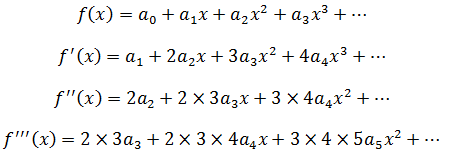
以三阶导数为例:
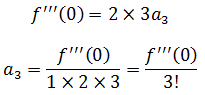
推广到n阶导数:
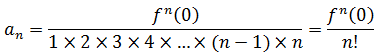
泰勒公式成立的条件是x处于收敛半径R的内部,即|x| < R。收敛半径是x的一段连续的取值范围,在收敛半径内,幂级数是收敛的;在收敛半径外,幂级数是发散的;如果|x| = R,幂级数的收敛性不确定。所谓在幂级数中收敛半径中收敛,就是当x < |R|时,必然有|anxn|→0,其判断条件是:

将收敛半径看成一个圆,x的取值点如果在圆内,则幂级数是收敛的,在圆外则是无意义的。当然,圆可以无穷大。
泰勒公式的应用
来看一个泰勒公式的应用。假设一个小偷偷了一辆汽车,他在高速公路上沿着一个方向行驶,车辆的位移S是关于时间t的函数。警方接到报案后马上调取监控,得知在零点(t = 0时刻)小偷距车辆丢失地点的位移是S0,现在的时间是0:30,警方想要做前方设卡,在凌晨1点拦住小偷,应该在哪里设卡呢?
我们知道在时刻位移是S0,现在想要知道凌晨1点时车辆的位置:
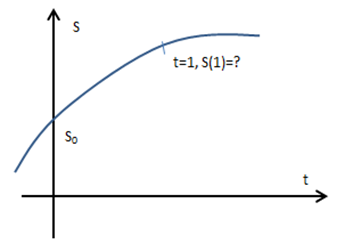
可以直接使用泰勒公式:

泰勒公式可以无限展开,展开的越多,越逼近真实值,并且越到后面的项,对结果的影响越小,所以通常只展开到二阶导数。
泰勒展开
如果一个函数有连续导数,那么这个函数就可以使用泰勒公式展开。
f(x) = ex是一个可以用泰勒公式展开的例子,下面是ex在x = 0处的泰勒展开:

当x = 1时,还附带得到了e的解释:
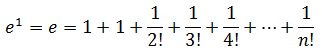
展开的意义——化质为量
我们使用一个很难处理的积分解释泰勒展开的意义,对正态分布进行积分:
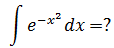
常规的方法很难处理。现在,由于被积函数与ex相似,我们又已经知道ex的展开式,所以可以进行下面的变换:
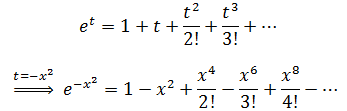
左右两侧同时积分:
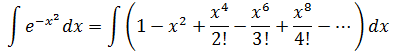
很容易计算右侧的积分。
这个例子展示了幂级数展开的意义——把质的困难转化成量的复杂。展开前求解函数的值很困难,展开后是幂级数,虽然有很多很多项,但是每一项都是幂函数,都很容易求解,于是,只要对展开后的函数求和,就能得到展开前的函数的值。
作者:我是8位的
出处:http://www.cnblogs.com/bigmonkey
本文以学习、研究和分享为主,如需转载,请联系本人,标明作者和出处,非商业用途!
扫描二维码关注公众号“我是8位的”
