cs231n-学习笔记-02线性分类

线性分类

0 介绍

线性分类可以自然的延伸到神经网络和卷积神经网络上。这种方法主要由两部分组成，

①评分函数（score function）

②损失函数（loss function）

评分函数是原始图像数据到类别分值的映射。损失函数是用来量化预测分类标签的得分与真实标签之间的一致性的。线性分类可以转化为一个最优化问题，在最优化的过程中，将通过更新评分函数的参数来最小化损失函数值。

将图像看做高维度的点

既然图像被伸展成为了一个高维度的列向量，那么我们就可以把图像看做这个高维度空间的一个点（即每张图像是3072维空间的一个点）。整个数据集就是一个点的集合，每个点都带有1个分类标签。

W的每一行都是一个分类类别的分类器。可以认为线性分类器是在高效利用KNN，不同的是我们没有使用所有的训练集图像做比较，而是每个类别只用一张图片（这张图片是我们学习到的，而不是训练集中的某一张图片）

线性分类器对于不同颜色的车的分类能力是很弱的，但是神经网络可以很好的完成这一任务。

图像数据预处理

所有图像原始的像素值是0-255。我们把图像中的每个像素看做一个特征，在实践中，对每个特征减去平均值来中心化数据非常重要的。这样图像的像素值基本分布在-127-127。采用零均值中心化，让所有数值分布的区间变为-1-1

参数方法

输入32x32x3(3072)大小的图像——————>f(x, W)———————>输出10个数字，表示给出的每个类别的评分

线性分类器： $f(x,W)=wX+b$

10x1 = 10x3072 * 3072x1 + 10x1

定义一个线性得分函数 $f(x,W)=wX+b$

损失函数：定义一个损失函数，用于量化我们对训练数据集只能不满的得分

优化器：想出一种有效地找到最小化损失函数的参数的方法

卷积网络：调整f的功能形式

1 损失函数

在给定数据集样本后，损失函数告诉我们当前的分类器有多好。

线性分类损失函数： $L=\frac{1}{N}\sum_{i}L_{i}(f(x_{i}, W), y_{i})$

多分类支持向量机损失函数：

\begin{aligned} L_{i} & = \sum_{j \neq y_{i}} {\begin{matrix} 0 & i f s_{y_{i}} ⩾ s_{j} + 1 \\ s_{j} - s_{y_{i}} + 1 & o t h e r w i s e \end{matrix} \\ = \sum_{j \neq y_{i}} m a x (0, s_{j} - s_{y_{i}} + 1) \end{aligned}

$\begin{align*} L_{i} & =\sum_{j\neq y_{i}}\left\{\begin{matrix} 0 & if s_{y_{i}} \geqslant s_{j}+1\\ s_{j}-s_{y_{i}}+1 & otherwise \end{matrix}\right. \\&=\sum_{j\neq y_{i}}max(0,s_{j}-s_{y_{i}}+1) \end{align*}$
称之为合页损失函数，合页损失函数不仅要分类正确，而且确信度足够高时损失才是0，也就是说，合页损失函数对学习有更高的要求。其图像如下：

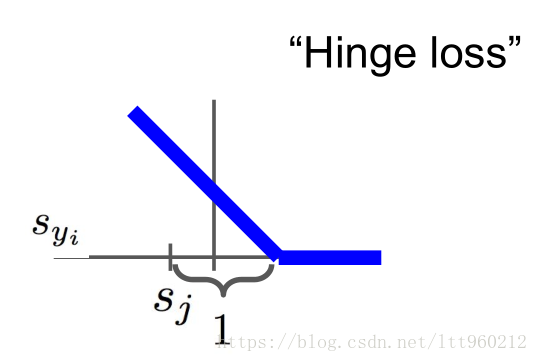
整个数据集上的损失函数： $L=\frac{1}{N}\sum_{i=1}^{N}L_{i}$

问题1：若汽车的得分稍微改变，对损失函数有什么影响？

损失函数将不会变化，正确分数比错误的分数大1，所以稍微的改变不会对最终的损失函数产生影响

问题2：损失函数的最小值最大值可能是多少？

最小值是0，最大值是无穷大

问题3：在训练初期，W非常小，接近0，当所有的分数都接近0，并且他们之间相差不大，当使用多分类支持向量机时，会发生怎么样的变化？

c-1,分类数-1

问题4：如果我们对所有错误的分数求和会发生什么？对所有正确的分数求和会发生什么？将所有的分数求和会发生什么呢？

损失函数增加了1

问题5：如果我们求这些分数的平均数而不是求和呢？

损失函数不会改变

问题6：要是在损失函数上加一个平方项 $L_{i}=\sum_{j\neq y_{i}}max(0,s_{j}-s_{y_{i}}+1)^{2}$

会变成一个不同的分类算法，采用一种非线性的方法，改变了在好喝坏之间的权衡

多分类支持向量机代码示例

$L_{i}=\sum_{j\neq y_{i}}max(0,s_{j}-s_{y_{i}}+1)$

def L_i_vectorized(x, y, W):
    scores = W.dot(x)
    margins = np.maximum(0, scores - scores[y] + 1)
    margins[y] = 0
    loss_i = np.sum(margins)
    return loss_i

$f(x,W)=Wx$

$L=\frac{1}{N}\sum_{i=1}^{N}\sum_{j\neq y_{i}}max(0,f(x_{i};W)_{j}-f(x_{i};W)_{y_{i}}+1)$

问：假设我们找到了一个使损失函数为0的权重矩阵W，这个W是唯一的吗？

答：不是，2W也能够使损失函数为0

损失函数

$L(W)=\frac{1}{N}\sum_{i=1}^{N}L_{i}(f(x_{i},W),y_{i})+ \lambda R(W)$

前部分和训练数据匹配，为了防止过拟合，后面加入正则项。

奥卡姆剃刀：在竞争假设中，最简单的就是最好的。

2 正则化

$\lambda$ =正则化强度，是一个超参数

对于损失函数，需要增加一个正则化项，如下所示：

$L=\frac{1}{N}\sum_{i=1}^{N}\sum_{j\neq y_{i}}max(0,f(x_{i};W)_{j}-f(x_{i};W)_{y_{i}}+1)+\lambda R(W)$

经常使用的正则化项：

①L1正则化： $R(W)=\sum_{k}\sum_{l}W_{k,l}^{2}$

②L2正则化： $R(W)=\sum_{k}\sum_{l}\left |W_{k,l} \right |$

③弹性网络（L1+L2）： $R(W)=\sum_{k}\sum_{l}\beta W_{k,l}^{2}+\left | W_{k,l} \right |$

④最大标准正则化

⑤dropout

⑥批标准化，stochastic depth(随机深度)

正则化最好的性质就是对大数值权重进行惩罚，可以提升其泛化能力，因为这就意味着没有哪个维度能够独自对整体分值有过大的影响。

因为正则化的存在，不可能在所有的例子中得到0的损失值，这是因为只有当W=0的特殊情况下，才能得到损失值0。

3 Softmax分类器

两个最常用的分类器：①SVM;②Softmax;

多项逻辑回归交叉熵损失函数

$P(Y=k|X=x_{i})=\frac{e^{s_{k}}}{\sum_{j}e^{s_{j}}}$ ,其中 $s=f(x_{i};W)$

想要让对数似然最大，或者（对于损失函数）最小化负的对数似然

$L_{i}=-logP(Y=y_{i}|X=x_{i})=-log(\frac{e^{s_{k}}}{\sum_{j}e^{s_{j}}})$ 分母为所有的j

问题1：softmax函数的最小值和最大值是多少？

最小值是0，最大值是无穷大

问题2：如果所有的得分都很小，损失值是多少？

-log(n)

问题3：假如我轻微的改变一个数据点的得分，softmax函数会发生什么样的变化？

发生比轻微更大的变化。softmax总是在提高每个数据点，使他们的分类越来越好。

小结

我们有一个数据集(x,y)

我们有一个评分函数 $s=f(x;W)=Wx$

我们有一些损失函数

$L_{i}=-log(\frac{e^{s_{k}}}{\sum_{j}e^{s_{j}}})$ softmax

$L_{i}=\sum_{j\neq y_{i}}max(0,s_{j}-s_{y_{i}}+1)$

$L=\frac{1}{N}\sum_{i=1}^{N}L_{i}+ R(W)$

我们怎么才能找到最好的权值W呢？优化的方法

4 优化

最优化是寻找能使得损失函数值最小化的参数W的过程。

概览：

一旦理解了参数函数的映射、损失函数和最优化的过程这三个部分是如何相互运作的，我们将回到第一部分（基于参数的函数映射），然后将其拓展为一个远比线性函数复杂的函数：首先是神经网络，然后是卷积神经网络。而损失函数和最优化过程这两个部分将会保持相对稳定。

损失函数可以量化某个具体权重集W的质量，而最优化的目标就是找到能够最小化损失函数值的W。

策略1：不好的解决方法，随机搜索

# X_train : (3073 x 50000)
# Y_train : (1 x 50000)
# L : 评估损失函数的好坏
bestloss = float("inf")  #  正无穷大
for num in xrange(1000):
    W = np.random.randn(10, 3073) * 0.0001  #  生成随机参数
    loss = L(X_train, Y_train, W)  #  计算整个数据集上的损失函数
    if loss < bestloss:  #  跟踪最好的损失函数
        bestloss = loss
        bestW = W
    print("in attempt %d the loss was %f, best %f" % (num, loss, bestloss)

#  评估在测试集上的表现
# X_test : (3073 x 10000)
# Y_test : (10000 x 1)
scores = Wbest.dot(Xte_cols)  #  10 x 10000
#  找出每列中最大得分的索引
Yte_predict = np.argmax(scores, axis=0)
#  计算精确度
np.mean(Yte_predict == Yte)   #  返回0.1555

核心思路：

我们的策略是从随机权重开始，然后迭代取优，从而获得更低的损失值。

策略2：沿着斜坡往下走

在一维中，函数的表示形式为： $\frac{\mathrm{d} f(x)}{\mathrm{d} x}=\lim_{h \to 0}\frac{f(x + h)-f(x)}{h}$

在多维中，梯度是每个维度的导数组成的向量

任何方向的斜率是该方向与梯度的点积

最陡下降的方向是负梯度

上面这种方法不好，使用微积分来计算梯度。

小结

数值梯度法：近似值，比较慢，比较容易计算。是一种缓慢计算的方法，实现相对简单。

分析梯度法：明确的，比较快，比较容易计算错误，且需要微分

在实践中，总是使用Analytic gradient计算梯度，但是使用Numerical gradient检查其实现过程。这就是所谓的梯度检查。

5 梯度下降

在梯度的负方向上更新，我们希望函数值是降低不是升高。

步长的影响：梯度指明了函数在哪个方向是变化率是最大的，但是没有指明在这个方向应该走多远。为此，需要选择步长（学习率）将会是神经网络中最重要也是最头痛的超参数设定之一。

使用数值梯度法计算梯度比较简单，但缺点终究是近似，且耗费太多的计算资源。分析梯度法利用微分来分析，能得到计算梯度的公式，用公式计算梯度很快，唯一不好的就是计算的时候容易出错。为了解决这个问题，在实际操作时，常常将分析梯度法的结果和数值梯度法的结果作比较，以此来检查其实现的正确性，这个步骤叫做梯度检查。

#  普通的梯度下降
while True:
    weights_grad = evaluate_gradient(loss_fun, data, weights)
    weights += - step_size * weights_grad  #  执行参数更新

随机梯度下降（SGD）

L (W) = \frac{1}{N} \sum_{i = 1}^{N} L_{i} (x_{i}, y_{i}, W) + λ R (W)

$L(W)=\frac{1}{N}\sum_{i=1}^{N}L_{i}(x_{i},y_{i},W)+\lambda R(W)$

▽_{W} L (W) = \frac{1}{N} \sum_{i = 1}^{N} ▽_{W} L_{i} (x_{i}, y_{i}, W) + λ ▽_{W} R (W)

$\triangledown _{W}L(W)=\frac{1}{N}\sum_{i=1}^{N}\triangledown _{W}L_{i}(x_{i},y_{i},W)+\lambda\triangledown _{W}R(W)$

当N很大时，全部求和的代价很大。通常采用的方式是使用小批的样本，常用的批处理大小为32/64/128

#  普通的批处理梯度下降
while True:
    data_batch = sample_training_data(data, 256) #  训练256个样本
    weights_grad = evaluate_gradient(loss_fun, data_batch, weights)
    weights += - step_size * weights_grad  #  执行参数更新