VAE的推导

参考文章《Auto-Encoding Variational Bayes》.
假设数据集是独立同分布（I.I.D），每个样本皆服从随机分布 $p(\cdot)$ ，数据集有N个样本。我们构造由N个随机变量构成的联合分布 $p(\mathbf x_1,\text{...},\mathbf x_N)=\prod_{i=1}^N p(\mathbf x_i)$ 。
从最大似然观点来看联合分布，当N个变量恰好是数据集样本（即：由抽样点组成的联合状态的概率）此时的联合分布的概率应取最大值。
对联合分布取对数似然，有：

\log p (x_{1}, ..., x_{N}) = \sum_{i = 1}^{N} \log p (x_{i}) (1)

$\log p(\mathbf x_1,\text{...},\mathbf x_N)=\sum_{i=1}^N \log p(\mathbf x_i) \qquad(1)$
因为Dataset背后的分布

P (\cdot)

$P(\cdot)$ 我们是不知道的，因而无法直接生成新的样本，这也是生成模型最终想要实现的目标。
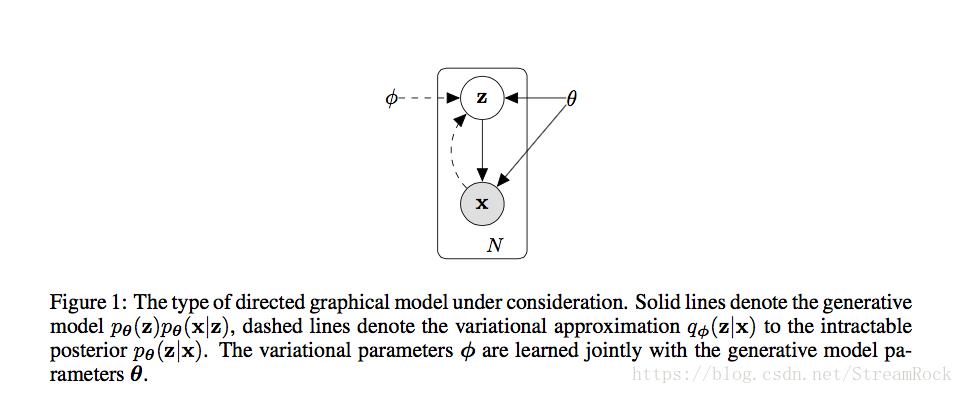
VAE(Variational Auto-Encoder)是一个生成模型，它为解决上述目标，引入了一个隐变量模型，如图：
这里写图片描述

原来的随机变量只有一个 $\mathbf x$ ，现在变成了两个随机变量的联合 $(\mathbf x, \mathbf z)$ ，原来的两个独立概率空间： $\mathbf x \in \mathbf X$ 和 $\mathbf z \in \mathbf Z$ ，变成了联合空间 $（\mathbf X \times \mathbf Z）$ 相应的边沿分布（Marginal Distribution）。构造该联合分布只有一个约束条件：要满足 $\mathbf x$ 这一侧的边沿分布为 $p(\mathbf x)$ ，对 $\mathbf z$ 没有要求，因而我们可以指定 $\mathbf z$ 的分布，比如：正态分布。
由Figure1，为简化推导，考虑连续随机变量，处理公式（1）有：

\log p (x_{i}) = \int_{z} q_{ϕ} (z | x_{i}) d z \cdot \log p (x_{i}) = \int_{z} q_{ϕ} (z | x_{i}) \cdot \log p (x_{i}) d z = \int_{z} q_{ϕ} (z | x_{i}) \cdot \log \frac{p (x_{i}) \cdot q_{ϕ} (z | x_{i}) \cdot p_{θ} (z | x_{i})}{q_{ϕ} (z | x_{i}) \cdot p_{θ} (z | x_{i})} d z = \int_{z} q_{ϕ} (z | x_{i}) \cdot \log \frac{p_{θ} (x_{i}, z) \cdot q_{ϕ} (z | x_{i})}{q_{ϕ} (z | x_{i}) \cdot p_{θ} (z | x_{i})} d z = \int_{z} q_{ϕ} (z | x_{i}) \cdot \log \frac{q_{ϕ} (z | x_{i})}{p_{θ} (z | x_{i})} d z + \int_{z} q_{ϕ} (z | x_{i}) \cdot \log \frac{p_{θ} (x_{i}, z)}{q_{ϕ} (z | x_{i})} d z (2)

$\log p(\mathbf x_i)=\int_{\mathbf z} q_{\phi}(\mathbf z \vert \mathbf x_i)d\mathbf z \cdot \log p(\mathbf x_i) =\int_{\mathbf z} q_{\phi}(\mathbf z \vert \mathbf x_i) \cdot \log p(\mathbf x_i) d\mathbf z \\ =\int_{\mathbf z}q_{\phi}(\mathbf z \vert \mathbf x_i) \cdot \log \frac {p(\mathbf x_i)\cdot q_{\phi}(\mathbf z \vert \mathbf x_i) \cdot p_{\theta}(\mathbf z \vert \mathbf x_i)}{q_{\phi}(\mathbf z \vert \mathbf x_i) \cdot p_{\theta}(\mathbf z \vert \mathbf x_i)}d\mathbf z \\ = \int_{\mathbf z}q_{\phi}(\mathbf z \vert \mathbf x_i) \cdot \log \frac {p_{\theta}(\mathbf x_i, \mathbf z)\cdot q_{\phi}(\mathbf z \vert \mathbf x_i)}{q_{\phi}(\mathbf z \vert \mathbf x_i) \cdot p_{\theta}(\mathbf z \vert \mathbf x_i)}d\mathbf z \\ =\int_{\mathbf z} q_{\phi}(\mathbf z \vert \mathbf x_i) \cdot \log \frac {q_{\phi}(\mathbf z \vert \mathbf x_i)}{p_{\theta}(\mathbf z \vert \mathbf x_i)}d \mathbf z \ + \ \int_{\mathbf z} q_{\phi}(\mathbf z \vert \mathbf x_i) \cdot \log \frac {p_{\theta}(\mathbf x_i , \mathbf z)}{q_{\phi}(\mathbf z \vert \mathbf x_i)}d \mathbf z \qquad(2)$
(2)式右边第一项为

D_{K L} (q_{ϕ} (z | x_{i}) ‖ p_{θ} (z | x_{i}))

$D_{KL}(q_{\phi}(\mathbf z \vert \mathbf x_i) \Vert p_{\theta}(\mathbf z \vert \mathbf x_i))$ ，令右边第二项为

L (θ, ϕ; x_{i})

$\mathcal L(\theta, \phi; \mathbf x_i)$ ，于是有：

\log p (x_{i}) = D_{K L} (q_{ϕ} (z | x_{i}) ‖ p_{θ} (z | x_{i})) + L (θ, ϕ; x_{i}) (3) L (θ, ϕ; x_{i}) = \int_{z} q_{ϕ} (z | x_{i}) \cdot \log \frac{p_{θ} (x_{i}, z)}{q_{ϕ} (z | x_{i})} d z (4)

$\log p(\mathbf x_i) = D_{KL}(q_{\phi}(\mathbf z \vert \mathbf x_i) \Vert p_{\theta}(\mathbf z \vert \mathbf x_i)) \ + \ \mathcal L(\theta, \phi; \mathbf x_i) \qquad(3) \\ \mathcal L(\theta, \phi; \mathbf x_i) = \ \int_{\mathbf z} q_{\phi}(\mathbf z \vert \mathbf x_i) \cdot \log \frac {p_{\theta}(\mathbf x_i , \mathbf z)}{q_{\phi}(\mathbf z \vert \mathbf x_i)}d \mathbf z \qquad(4)$
因为KL散度大于等于0，因此

L (θ, ϕ; x_{i})

$\mathcal L(\theta, \phi; \mathbf x_i)$ 是

\log p (x_{i})

$\log p(\mathbf x_i)$ 的下界。VAE将优化这个下界，进行近似推断（Approximate Inference），后续过程就是通过

L (θ, ϕ; x)

$\mathcal L(\theta, \phi; \mathbf x)$ 对

θ

$\theta$ 和

ϕ

$\phi$ 求梯度，使

L (θ, ϕ; x)

$\mathcal L(\theta, \phi; \mathbf x)$ 获得最大值的过程。
由(4)有

L (θ, ϕ; x_{i}) = \int_{z} q_{ϕ} (z | x_{i}) \cdot \log \frac{p_{θ} (x_{i}, z)}{q_{ϕ} (z | x_{i})} d z = - \int_{z} q_{ϕ} (z | x_{i}) \cdot \log \frac{q_{ϕ} (z | x_{i})}{p_{θ} (x_{i}, z)} d z = - \int_{z} q_{ϕ} (z | x_{i}) \cdot \log \frac{q_{ϕ} (z | x_{i})}{p_{θ} (x_{i} | z) \cdot p_{θ} (z)} d z = - \int_{z} q_{ϕ} (z | x_{i}) \cdot \log \frac{q_{ϕ} (z | x_{i})}{p_{θ} (z)} d z + \int_{z} q_{ϕ} (z | x_{i}) \cdot \log p_{θ} (x_{i} | z) d z = - D_{K L} (q_{ϕ} (z | x_{i}) ‖ p_{θ} (z)) + E_{q_{ϕ} (z | x_{i})} [\log p_{θ} (x_{i} | z)] (5)

$\mathcal L(\theta, \phi; \mathbf x_i) = \ \int_{\mathbf z} q_{\phi}(\mathbf z \vert \mathbf x_i) \cdot \log \frac {p_{\theta}(\mathbf x_i , \mathbf z)}{q_{\phi}(\mathbf z \vert \mathbf x_i)}d \mathbf z \\ = -\int_{\mathbf z} q_{\phi}(\mathbf z \vert \mathbf x_i) \cdot \log \frac {q_{\phi}(\mathbf z \vert \mathbf x_i)}{p_{\theta}( \mathbf x_i , \mathbf z)}d \mathbf z \\ = -\int_{\mathbf z} q_{\phi}(\mathbf z \vert \mathbf x_i) \cdot \log \frac {q_{\phi}(\mathbf z \vert \mathbf x_i)}{p_{\theta}( \mathbf x_i \vert \mathbf z) \cdot p_{\theta}( \mathbf z )}d \mathbf z \\ = -\int_{\mathbf z} q_{\phi}(\mathbf z \vert \mathbf x_i) \cdot \log \frac {q_{\phi}(\mathbf z \vert \mathbf x_i)}{p_{\theta}(\mathbf z )}d \mathbf z \ + \ \int_{\mathbf z} q_{\phi}(\mathbf z \vert \mathbf x_i) \cdot \log p_{\theta}(\mathbf x_i \vert \mathbf z ) d \mathbf z \\ = -D_{KL}(q_{\phi}(\mathbf z \vert \mathbf x_i) \Vert p_{\theta}(\mathbf z)) \ + \ \mathbf E_{q_{\phi}(\mathbf z \vert \mathbf x_i)}[\log p_{\theta}(\mathbf x_i \vert \mathbf z)] \qquad(5)$
(5)式第一项反映的是隐变量

z

$\mathbf z$ 的分布

p_{θ} (x)

$p_{\theta}(\mathbf x)$ 与给定

x_{i}

$\mathbf x_i$ 的真实后验分布的近似分布

q_{ϕ} (z | x_{i})

$q_{\phi}(\mathbf z \vert \mathbf x_i)$ 距离。第二项反映自动编码器的（Auto-Encoder-Decoder）性能：

x_{i} \to z \to x_{i}

$\mathbf x_i \to \mathbf z \to \mathbf x_i$ ，即经过编码和解码后，取该样本

x_{i}

$\mathbf x_i$ 的概率平均值。若批处理所选择的样本数量较大时，可以取L=1，即对于每个样本

x_{i}

$\mathbf x_i$ ，每次批处理训练时只抽一次。
在前面的推导过程中，我们并没有给出关于

p_{θ} (z)

$p_{\theta}(\mathbf z)$ 和

q_{ϕ} (z | x_{i})

$q_{\phi}(\mathbf z \vert \mathbf x_i)$ 的任何约束条件。假设

p_{θ} (z)

$p_{\theta}(\mathbf z)$ 是J维标准正态分布：

N (z; 0, I)

$N(\mathbf z;\mathbf 0, \mathbf I)$ ，

q_{ϕ} (z | x_{i})

$q_{\phi}(\mathbf z \vert \mathbf x_i)$ 是与之形状相似的J维正态分布，其协方差矩阵是对角阵，有

N (z; μ, σ)

$N(\mathbf z; \mathbf {\mu}, \mathbf {\sigma})$ ，

μ_{i}

$\mu_i$ 和

σ_{i}

$\sigma_i$ 分别为期望矢量

μ

$\mathbf \mu$ 和方差矢量

σ

$\mathbf \sigma$ 的各单元的值。于是(5)式等号右边第一项的KL散度可以给出解析解，因为：

\int_{z} q_{ϕ} (z) \cdot \log p_{θ} (z) d z = \int N (z; μ, σ) \log N (z; 0, I) d z = - \frac{J}{2} \log (2 π) - \frac{1}{2} \sum_{i = 1}^{J} (μ_{i}^{2} + σ_{i}^{2}) \int_{z} q_{ϕ} (z) \cdot \log q_{ϕ} (z) d z = \int N (z; μ, σ) \log N (z; μ, σ) d z = - \frac{J}{2} \log (2 π) - \frac{1}{2} \sum_{i = 1}^{J} (1 + \log σ_{i}^{2})

$\int_{\mathbf z} q_{\phi}(\mathbf z) \cdot \log p_{\theta}(\mathbf z)d \mathbf z = \int N(\mathbf z; \mathbf {\mu}, \mathbf {\sigma}) \log N(\mathbf z;\mathbf 0, \mathbf I)d \mathbf z\\ = -\frac J 2 \log(2\pi) - \frac 1 2 \sum_{i=1}^J (\mu_i^2 + \sigma_i^2) \\ \int_{\mathbf z} q_{\phi}(\mathbf z) \cdot \log q_{\phi}(\mathbf z)d \mathbf z = \int N(\mathbf z; \mathbf {\mu}, \mathbf {\sigma}) \log N(\mathbf z; \mathbf {\mu}, \mathbf {\sigma})d \mathbf z\\ = -\frac J 2 \log(2\pi) - \frac 1 2 \sum_{i=1}^J (1 + \log \sigma_i^2)$
因此，有：

- D_{K L} (q_{ϕ} (z | x_{i}) ‖ p_{θ} (z)) = \frac{1}{2} \sum_{i = 1}^{J} (1 + \log σ_{i}^{2} - μ_{i}^{2} - σ_{i}^{2}) (5)

$-D_{KL}(q_{\phi}(\mathbf z \vert \mathbf x_i) \Vert p_{\theta}(\mathbf z)) = \frac 1 2 \sum_{i=1}^J (1 + \log \sigma_i^2 - \mu_i^2 -\sigma_i^2) \qquad(5)$
(5)式等号右边第二项，需要通过Monte Carlo方法获得，即：

E_{q_{ϕ} (z | x_{i})} [\log p_{θ} (x_{i} | z)] = \frac{1}{L} \sum_{l = 1}^{L} \log p_{θ} (x_{i} | z_{i}^{l}) (6)

$\mathbf E_{q_{\phi}(\mathbf z \vert \mathbf x_i)}[\log p_{\theta}(\mathbf x_i \vert \mathbf z)] = \frac 1 L \sum_{l=1}^L \log p_{\theta}(\mathbf x_i \vert \mathbf z_i^l ) \qquad(6)$
当L=1时，

E_{q_{ϕ} (z | x_{i})} [\log p_{θ} (x_{i} | z)] = \log p_{θ} (x_{i} | z_{i}) (7)

$\mathbf E_{q_{\phi}(\mathbf z \vert \mathbf x_i)}[\log p_{\theta}(\mathbf x_i \vert \mathbf z)] = \log p_{\theta}(\mathbf x_i \vert \mathbf z_i ) \qquad(7)$
于是，最终有：

L (θ, ϕ; x_{i}) = \frac{1}{2} \sum_{i = 1}^{J} (1 + \log σ_{i}^{2} - μ_{i}^{2} - σ_{i}^{2}) + \log p_{θ} (x_{i} | z_{i}) (8) \log p (x_{1}, ..., x_{N}) = \sum_{i = 1}^{N} \log p (x_{i}) \geq \frac{N}{M} \sum_{i = 1}^{M} L (θ, ϕ; x_{i}) (9)

$\mathcal L(\theta, \phi; \mathbf x_i) = \frac 1 2 \sum_{i=1}^J (1 + \log \sigma_i^2 - \mu_i^2 -\sigma_i^2) + \log p_{\theta}(\mathbf x_i \vert \mathbf z_i )\qquad(8)\\\log p(\mathbf x_1,\text{...},\mathbf x_N)=\sum_{i=1}^N \log p(\mathbf x_i) \ge \frac N M \sum_{i=1}^M \mathcal L(\theta, \phi; \mathbf x_i) \qquad(9)$
（9）式中N是数据集样本的总的个数，M是mini-batch中，每一批次训练样本的个数。为求最大似然，我们抬高最大似然的下界。该下界获得最大值的地方，我们就认为在该处取得了最大似然，这是一个近似推断。
因为一般的后向梯度处理得到的是最小值，因而，训练所用Loss需要对

L

$\mathcal L$ 取反。以下VAE实现摘抄自：
https://github.com/pytorch/examples/blob/master/vae/main.py

from __future__ import print_function
import argparse
import torch
import torch.utils.data
from torch import nn, optim
from torch.nn import functional as F
from torchvision import datasets, transforms
from torchvision.utils import save_image


parser = argparse.ArgumentParser(description='VAE MNIST Example')
parser.add_argument('--batch-size', type=int, default=128, metavar='N',
                    help='input batch size for training (default: 128)')
parser.add_argument('--epochs', type=int, default=10, metavar='N',
                    help='number of epochs to train (default: 10)')
parser.add_argument('--no-cuda', action='store_true', default=False,
                    help='enables CUDA training')
parser.add_argument('--seed', type=int, default=1, metavar='S',
                    help='random seed (default: 1)')
parser.add_argument('--log-interval', type=int, default=10, metavar='N',
                    help='how many batches to wait before logging training status')
args = parser.parse_args()
args.cuda = not args.no_cuda and torch.cuda.is_available()


torch.manual_seed(args.seed)

device = torch.device("cuda" if args.cuda else "cpu")

kwargs = {'num_workers': 1, 'pin_memory': True} if args.cuda else {}
train_loader = torch.utils.data.DataLoader(
    datasets.MNIST('../data', train=True, download=True,
                   transform=transforms.ToTensor()),
    batch_size=args.batch_size, shuffle=True, **kwargs)
test_loader = torch.utils.data.DataLoader(
    datasets.MNIST('../data', train=False, transform=transforms.ToTensor()),
    batch_size=args.batch_size, shuffle=True, **kwargs)


class VAE(nn.Module):
    def __init__(self):
        super(VAE, self).__init__()

        self.fc1 = nn.Linear(784, 400)
        self.fc21 = nn.Linear(400, 20)
        self.fc22 = nn.Linear(400, 20)
        self.fc3 = nn.Linear(20, 400)
        self.fc4 = nn.Linear(400, 784)

    def encode(self, x):
        h1 = F.relu(self.fc1(x))
        return self.fc21(h1), self.fc22(h1)

    def reparameterize(self, mu, logvar):
        if self.training:
            std = torch.exp(0.5*logvar)
            eps = torch.randn_like(std)
            return eps.mul(std).add_(mu)
        else:
            return mu

    def decode(self, z):
        h3 = F.relu(self.fc3(z))
        return F.sigmoid(self.fc4(h3))

    def forward(self, x):
        mu, logvar = self.encode(x.view(-1, 784))
        z = self.reparameterize(mu, logvar)
        return self.decode(z), mu, logvar


model = VAE().to(device)
optimizer = optim.Adam(model.parameters(), lr=1e-3)


# Reconstruction + KL divergence losses summed over all elements and batch
def loss_function(recon_x, x, mu, logvar):
    BCE = F.binary_cross_entropy(recon_x, x.view(-1, 784), size_average=False)

    # see Appendix B from VAE paper:
    # Kingma and Welling. Auto-Encoding Variational Bayes. ICLR, 2014
    # https://arxiv.org/abs/1312.6114
    # 0.5 * sum(1 + log(sigma^2) - mu^2 - sigma^2)
    KLD = -0.5 * torch.sum(1 + logvar - mu.pow(2) - logvar.exp())

    return BCE + KLD


def train(epoch):
    model.train()
    train_loss = 0
    for batch_idx, (data, _) in enumerate(train_loader):
        data = data.to(device)
        optimizer.zero_grad()
        recon_batch, mu, logvar = model(data)
        loss = loss_function(recon_batch, data, mu, logvar)
        loss.backward()
        train_loss += loss.item()
        optimizer.step()
        if batch_idx % args.log_interval == 0:
            print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
                epoch, batch_idx * len(data), len(train_loader.dataset),
                100. * batch_idx / len(train_loader),
                loss.item() / len(data)))

    print('====> Epoch: {} Average loss: {:.4f}'.format(
          epoch, train_loss / len(train_loader.dataset)))


def test(epoch):
    model.eval()
    test_loss = 0
    with torch.no_grad():
        for i, (data, _) in enumerate(test_loader):
            data = data.to(device)
            recon_batch, mu, logvar = model(data)
            test_loss += loss_function(recon_batch, data, mu, logvar).item()
            if i == 0:
                n = min(data.size(0), 8)
                comparison = torch.cat([data[:n],
                                      recon_batch.view(args.batch_size, 1, 28, 28)[:n]])
                save_image(comparison.cpu(),
                         'results/reconstruction_' + str(epoch) + '.png', nrow=n)

    test_loss /= len(test_loader.dataset)
    print('====> Test set loss: {:.4f}'.format(test_loss))


for epoch in range(1, args.epochs + 1):
    train(epoch)
    test(epoch)
    with torch.no_grad():
        sample = torch.randn(64, 20).to(device)
        sample = model.decode(sample).cpu()
        save_image(sample.view(64, 1, 28, 28),
                   'results/sample_' + str(epoch) + '.png')

VAE分两部分网络实现，编码器（Encoder）得到的是 $q_{\phi}(\mathbf z \vert \mathbf x_i)$ 的充分统计量 $\mathbf \mu$ 和 $\mathbf \sigma$ ，而解码器（Decoder）得到的是重建图 $\tilde {\mathbf x_i}$ ，其过程是：
1、输入样本x_i，由编码器网络forward，得到 $q_{\phi}(\mathbf z \vert \mathbf x_i)$ 的充分统计量 $\mathbf \mu$ 和 $\mathbf \sigma$ ；
2、由此正态分布 $q_{\phi}(\mathbf z \vert \mathbf x_i)$ 抽样得到 $\mathbf z_i$ ；
3、解码器网络输入 $\mathbf z_i$ ，得到重构样本 $\tilde {\mathbf x_i}$ ；
4、由原图与重构图的逐位二进制交叉熵加上一个正则项： $-D_{KL}(q_{\phi}(\mathbf z \vert \mathbf x_i) \Vert p_{\theta}(\mathbf z)) = \frac 1 2 \sum_{i=1}^J (1 + \log \sigma_i^2 - \mu_i^2 -\sigma_i^2)$ ，得到最后训练用的Loss；
5、Loss后向梯度传播，修正两个网络的参数，迭代若干次，得到网络的最佳参数。

由上代码可见（8）式中的 $\log p_{\theta}(\mathbf x_i \vert \mathbf z_i )$ 表示的是输入样本 $\mathbf x_i$ 在概率密度 $p_{\theta}(\cdot \vert \mathbf z_i )$ 下取值的对数，此概率密度由Decoder输出，而在上述实现中，它是由重建图(recon_x)与原图(x)逐位二进制交叉熵来实现的：

def loss_function(recon_x, x, mu, logvar):
    BCE = F.binary_cross_entropy(recon_x, x.view(-1, 784), size_average=False)

    # see Appendix B from VAE paper:
    # Kingma and Welling. Auto-Encoding Variational Bayes. ICLR, 2014
    # https://arxiv.org/abs/1312.6114
    # 0.5 * sum(1 + log(sigma^2) - mu^2 - sigma^2)
    KLD = -0.5 * torch.sum(1 + logvar - mu.pow(2) - logvar.exp())

    return BCE + KLD

为什么：重建图(recon_x)与原图(x)逐位二进制交叉熵可以代表 $-\log p_{\theta}(\mathbf x_i \vert \mathbf z_i )$ ？在附录中，文章有一个简单的交代：
这里写图片描述
上述实现代码采用的是C1方法，因而用二进制交叉熵来代表 $-\log p_{\theta}(\mathbf x_i \vert \mathbf z_i )$ 。
上例，采用mnist作为输入样本，则Decoder输出的是多维0-1分布（伯努利分布）逐位（element-wise）像素 $x_i^l=1,l \in \{1,784\}$ 的概率（输出重建位图共有 $28 \times 28 = 784$ 位），设每一位相互独立，因而：

\log p_{θ} (x_{i} | z_{i}) = \sum_{l = 1}^{784} \log p_{θ} (x_{i}^{l} | z) (10)

$\log p_{\theta}(\mathbf x_i \vert \mathbf z_i)=\sum_{l=1}^{784} \log p_{\theta}(x_i^l \vert \mathbf z) \qquad(10)$
（10）式中，

x_{i}^{l}

$x_i^l$ 表示样本

x_{i}

$\mathbf x_i$ 的第 l 位。然而0-1分布是离散分布，给出的概率不是概率密度，可以从线性插值的角度来解释：
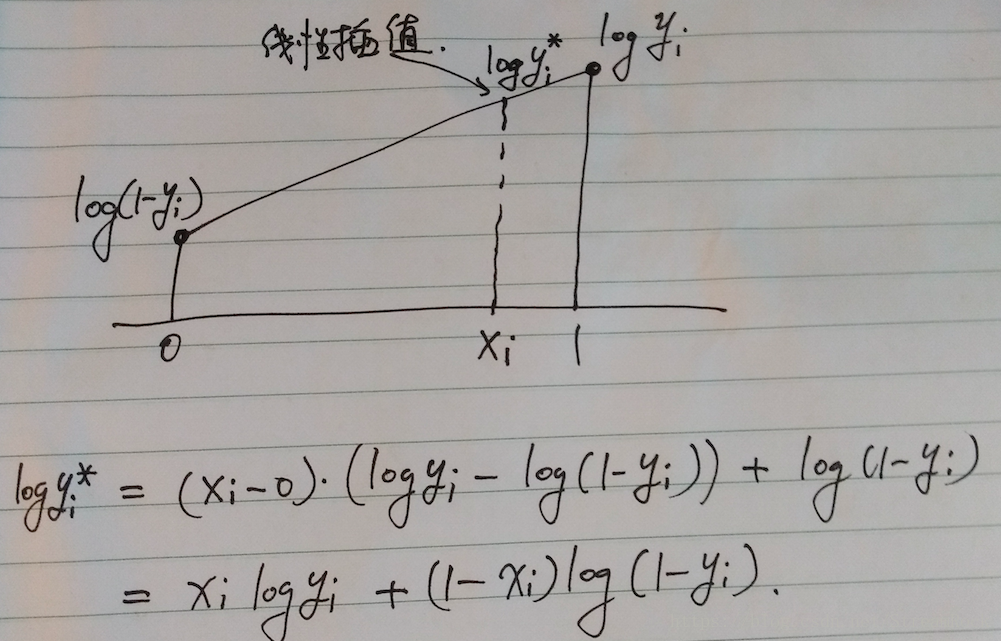
这里写图片描述

由于输出是0-1分布，因此Decoder预测的是0和1的概率，0-1分布本来是离散的，其概率密度可写为：

p (x_{i} | z) = y_{i} δ (1 - x) + (1 - y_{i}) δ (x) (11) \log p (x_{i} | z) = \log y_{i} \cdot δ (1 - x) + \log (1 - y_{i}) \cdot δ (x) (12)

$p(x_i \vert \mathbf z) = y_i\delta(1-x)+(1-y_i)\delta(x) \qquad(11) \\ \log p(x_i \vert \mathbf z) = \log y_i \cdot \delta(1-x) \ + \ \log (1-y_i )\cdot \delta(x) \qquad(12)$
其中，是

δ (x)

$\delta(x)$ 狄利克雷函数，

y_{i}

$y_i$ 是Decoder输出，即位置i为1的概率。对于任意

x_{i} \in [0, 1]

$x_i \in [0,1]$ 的对数概率值

p (x_{i} | z)

$p(x_i \vert \mathbf z)$ ，由其线性插值为：

p (x_{i} | z) = (x_{i} - 0) \cdot (\log y_{i} - \log (1 - y_{i})) + \log (1 - y_{i}) = x_{i} \cdot \log y_{i} + (1 - x_{i}) \cdot \log (1 - y_{i}) (13)

$p(x_i \vert \mathbf z) = (x_i -0)\cdot(\log y_i - \log (1-y_i )) + \log (1-y_i ) \\ = x_i \cdot \log y_i + (1-x_i) \cdot \log (1-y_i) \qquad(13)$
因而，我们可以用二进制交叉熵来实现（8）式的第二项。

猜你喜欢