计算几何总结（Part 1~2）

Preface

对于一个初三~~连三角函数都不会的蒟蒻~~来说计算几何简直就是噩梦。

~~反正都是要学的也TM没办法~~，那就慢慢一点点学起吧。

计算几何要有正确的板子，不然那种几百行CODE的题写死你。

本蒟蒻的学习过程参考dalao's blog和lrj的蓝书

Part 1——基本结构命名与精度控制

~~首先计算几何就是在一个坐标系内搞来搞去的鬼畜东西，~~因此点是必不可少的

定义点，还是最普通的坐标表示法：

struct Point
{
    DB x,y;
    Point (DB X=0,DB Y=0) { x=X; y=Y; }
};

然后就是一个比较牛逼的东西了——向量，根据高中数学必修3上讲的，我们也使用坐标的方式表示一个向量。

说的请楚一点，因为我们知道可以用两个不共线的向量表示同一平面内的任意向量，因此我们把每一个向量\(\vec a\)都分解成\(x\vec i+y\vec j\)(\(\vec i,\vec j\)是单位向量)的形式并且\((x,y)\)就是这个向量的坐标。

由于都可以用坐标表示，我们就直接借用点的表示方法了。

typedef Point Vector;

然而计算几何中有一个不可避免的问题：精度，所以适当的控制精度还是很需要的。

因此我们手动搞一个\(EPS\)，由我们熟知的：

\(|a|<EPS \rightarrow a=0\)
\(a<-EPS \rightarrow a<0\)
\(a\ge EPS \rightarrow a>0\)

我们就可以写一个代码来判断一个数的零的关系（返回\(-1,0,1\)）

inline int dcmp(DB x)
{
    if (fabs(x)<EPS) return 0;
    return x<-EPS?-1:1;
}

Part 2——点和向量之间的基本运算

一般运算符：

inline Vector operator + (Vector A,Vector B) { return Vector(A.x+B.x,A.y+B.y); }
inline Vector operator - (Point A,Point B) { return Vector(A.x-B.x,A.y-B.y); }
//inline Vector operator - (Vector A,Vector B) { return Vector(A.x-B.x,A.y-B.y); }
inline Vector operator * (Vector A,DB mul) { return Vector(A.x*mul,A.y*mul); }
inline Vector operator / (Vector A,DB div) { return Vector(A.x/div,A.y/div); }

注意一下：向量+向量=向量，点-点=向量（不过其实怎么定义都是一样的）

以及比较两个向量的运算符（个人习惯写在结构体里，这里的Point其实都是Vector的意思）：

    inline bool operator < (const Point A) const { return dcmp(x-A.x)?x<A.x:y<A.y; }
    inline bool operator == (const Point A) const { return !dcmp(x-A.x)&&!dcmp(y-A.y); }

求一个向量的模长，即向量的长度：

inline DB Len(Vector A)
{
    return sqrt(A.x*A.x+A.y*A.y);
}

求极角，这个直接用\(atan2(y,x)\)就可以求出\(\vec a(x,y)\)的极角了

inline DB Polar_Angle(Vector A)
{
    return atan2(A.y,A.x);
}

点积，根据数学书上说的，\(\vec a \cdot\vec b\)的几何意义为\(\vec a\)在\(\vec b\)上的投影长度乘以\(\vec b\)的模长

用公式表述为：\(\vec a\cdot \vec b=|\vec a|\cdot |\vec b|\cdot \cos\ \theta)\)(\(\theta\)为\(\vec a,\vec b\)之间的夹角)

在坐标表示下就是\(\vec a(x1,y1)\cdot \vec b(x2,y2)=x1\cdot x2+y1\cdot y2\)

inline DB Dot(Vector A,Vector B)
{
    return A.x*B.x+A.y*B.y;
}

点积的应用有很多，以下列举一些常用的：

判断两个向量的前后（上下）关系

例如对于以下的向量\(\vec a\)，如果另一个向量在红色区域时点积为正，在黄色区域时点积为负

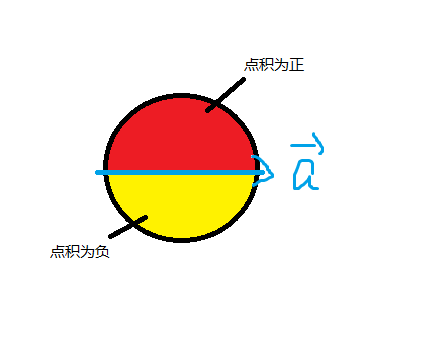
判断两个向量是否垂直：\(\vec a \perp \vec b \Leftrightarrow \vec a \cdot \vec b\)
求两个向量的夹角，这个把点积的定义公式变形一下就好了：
```
inline DB Angle(Vector A,Vector B)
{
  return acos(Dot(A,B)/Len(A)/Len(B));
}
```
求模长，这里可以用另一种方法求模长，即\(|\vec a|=\sqrt{(\vec a)^2}\)：
```
inline DB Len(Vector A)
{
  return sqrt(Dot(A,A));
}
```

向量的旋转，这个就是一个公式套上去

\(\vec a(x,y)\)可以看成是\(x\cdot(1,0)+y\cdot(0,1)\)(\((1,0)\)即为\(\vec i\),\((0,1)\)即为\(\vec j\))

分别旋转两个单位向量，则变成\(x\cdot(cos\ \theta,sin\ \theta)+y\cdot(-sin\ \theta,cos\ \theta)\)

inline Vector Rotate(Vector A,DB rad)
{
    DB Cos=cos(rad),Sin=sin(rad);
    return Vector(A.x*Cos-A.y*Sin,A.x*Sin+A.y*Cos);
}

法向量，与单位向量垂直的向量称为单位法向量，注意使用之前要判断这个向量是否为零

inline Vector Normal(Vector A)
{
    DB l=Len(A); return Vector(-A.y/l,A.x/l);
}

叉积，又是根据数学书上说的，两个向量的叉积是一个标量，\(\vec a\times \vec b\)的几何意义为他们所形成的平行四边形的有向面积

注意面积是有向的，一个公式\(\vec a(x1,y1)\times \vec b(x2,y2)=x1\cdot y2-x2\cdot y1\)

inline DB Cross(Vector A,Vector B)
{
    return A.x*B.y-A.y*B.x;
}

叉积的应用有很多，以下列举一些常用的：

判断两个向量的左右关系

例如对于以下的向量\(\vec a\)，如果另一个向量在红色区域时叉积为正，在黄色区域时叉积为负

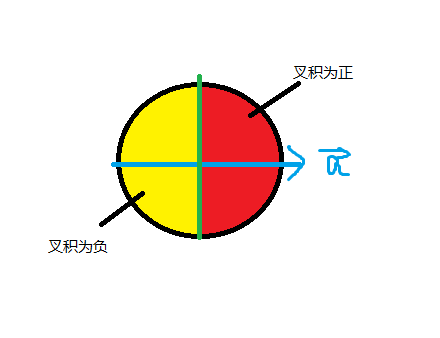
求三角形甚至是多边形的面积
求点到线段或者直线的距离
判断两个线段或者直线是否相交，并可以求交点
其它的很多东西，可以说叉积是整个计算几何的核心内容，这些我们下次再讲

Postscript

计算几何虽然以代码复杂，巨卡精度而闻名，但是学还是要学的~~不知道联赛考不考~~

争取近一个月都抽出点时间记录一下吧，接下来上Part1~2的所有模板CODE

#include<cstdio>
#include<cmath>
typedef double DB;
const DB EPS=1e-8;
inline int dcmp(DB x)
{
    if (fabs(x)<EPS) return 0;
    return x<-EPS?-1:1;
}
struct Point
{
    DB x,y;
    Point (DB X=0,DB Y=0) { x=X; y=Y; } 
    inline bool operator < (const Point A) const { return dcmp(x-A.x)?x<A.x:y<A.y; }
    inline bool operator == (const Point A) const { return !dcmp(x-A.x)&&!dcmp(y-A.y); }
};
typedef Point Vector;
inline Vector operator + (Vector A,Vector B) { return Vector(A.x+B.x,A.y+B.y); }
inline Vector operator - (Point A,Point B) { return Vector(A.x-B.x,A.y-B.y); }
//inline Vector operator - (Vector A,Vector B) { return Vector(A.x-B.x,A.y-B.y); }
inline Vector operator * (Vector A,DB mul) { return Vector(A.x*mul,A.y*mul); }
inline Vector operator / (Vector A,DB div) { return Vector(A.x/div,A.y/div); }
inline DB Dot(Vector A,Vector B)
{
    return A.x*B.x+A.y*B.y;
}
/*inline DB Len(Vector A)
{
    return sqrt(A.x*A.x+A.y*A.y);
}*/
inline DB Len(Vector A)
{
    return sqrt(Dot(A,A));
}
inline DB Cross(Vector A,Vector B)
{
    return A.x*B.y-A.y*B.x;
}
inline DB Polar_Angle(Vector A)
{
    return atan2(A.y,A.x);
}
inline DB Angle(Vector A,Vector B)
{
    return acos(Dot(A,B)/Len(A)/Len(B));
}
inline Vector Rotate(Vector A,DB rad)
{
    DB Cos=cos(rad),Sin=sin(rad);
    return Vector(A.x*Cos-A.y*Sin,A.x*Sin+A.y*Cos);
}
inline Vector Normal(Vector A)
{
    DB l=Len(A); return Vector(-A.y/l,A.x/l);
}