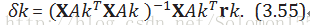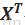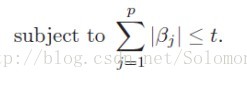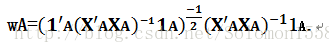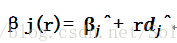LARS算法的几何意义

1. LARS算法简介

Efron于2004年发表在Annals of Statistics的文章LEAST ANGLE REGRESSION中提出LARS算法，其核心思想是提出一种新的solution path(求解路径)，即在已经入选的变量中，寻找一个新的路径，使得在这个路径上前进时，当前残差与已入选变量的相关系数都是相同的，直到找出新的比当前残差相关系数最大的变量。从几何上来看，当前残差在那些已选入回归集的变量们所构成的空间中的投影，是这些变量的角平分线。

2. LARS算法思路

以下算法出自The Elementsof Statistical Learning 书中第3章。

Algorithm LeastAngle Regression.

1.Standardize the predictors to have mean zero and unit norm. Startwiththe residualr=y–y^,β1, β2, .. . , βp= 0.

将样本中心化，标准化。残差向量 r = y – y^ ,系数β初始化为0.

2.Find the predictorxjmostcorrelated withr.

寻找与残差向量相关系数最大的样本变量 .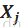

3.Moveβjfrom0 towards its least-squares coefficient<xj,r>,until someothercompetitorxkhasas much correlation with the current residualasdoesxj.

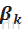
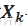
系数沿最小二乘解的方向增大，直到另一个样本变量与残差的相关系数与当前的一样大。

4.Moveβjand βk in the directiondefined by their joint least squarescoefficient ofthe current residual on

(xj,xk),until some other competitorxlhasas much correlation with the current residual.

游走点改变前进路径，沿着X1、X2的角平分线方向继续移动，直到其他变量X与残差r的相关系数与当前系数一样大。

5.Continue in this way until allppredictorshave been entered. Aftermin(N−1, p)steps, we arrive at the full least-squares solution.

继续沿着这种方式前进，直到所有的p个变量都已经加入活动集。

最终，所有变量都被选中，且残差向量r垂直于所以变量，求得最小二乘解。

3. LARS算法的几何意义

SupposeAkis the activeset of variables at the beginning of thekth step, and letβAkbe thecoefficient vector for these variables at this step; there will bek−1 nonzerovalues, and the one just entered will be zero.

If rk=y−XAkβAkis the currentresidual, then the direction for this step is

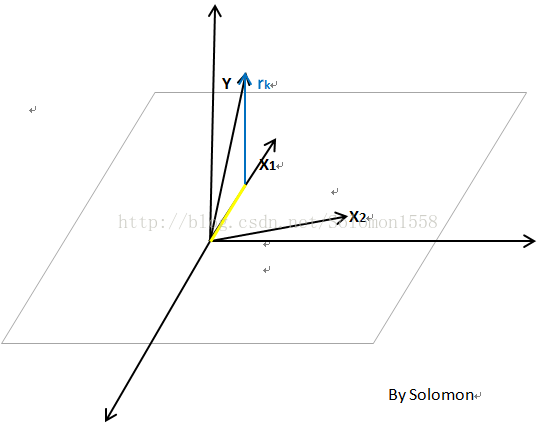
假设样本共有3个3维变量(即矩阵中n=p=3),其中Y是因变量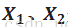，是两个三维因变量。

作图解释LARS算法的集合意义：

(1)Ak表示已选变量集合,在第1步中，选取与rk相关系数最大的变量(假设是X1)此时Ak集合中只有一个变量；

rk=y−XakβAk,表示当前变量集合下的残差向量；

沿向量X1的路径前进，X1与残差rk的相关系数逐渐减小。

(2) 当残差向量rk与X1的相关系数减少至与rk与X2的相关系数相等时，将X2加入Ak集合。此时XAk就是向量X1、X2所张成的平面。

此时需要重新选择solution path(求解路径)。Efron在文章中提出了一种找出满足LARS条件的solution path的解法。

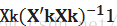
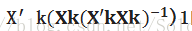
solution path需要使得已选入模型变量和当前残差的相关系数均相等。因此这样的路径选择它的方向很显然就是的指向(因为的元素都相同，保证了LARS的要求。

【注】此式中的X′即表示

综上，δk是指在加入新的变量X后，X与Y的残差的相关系数的估计，也就是图中角δk的余弦函数。(样本已经过中心化、标准化处理)

The coefficientprofile then evolves asβAk(α) =βAk+α·δk. Exercise 3.23 verifies that the directions chosen in this fashion dowhat is claimed: keep the correlations tied and decreasing. If the fit vectorat the beginning of this step is ˆfk, then itevolves as ˆfk(α) = fk+α·uk, whereuk=XAkδk is the new fit direction. The name “least angle” arises froma geometrical interpretation of this process;ukmakes thesmallest (and equal) angle with each of the predictors inAk(Exercise 3.24).

以上一段说明了LARS中“最小角”的几何含义：

所选路径必须保证已选入模型变量和当前残差的相关系数均最小且相等。因此需要选择旧路径与新变量夹角的角平分线方向作为新的路径方向。

4. Lasso 简介

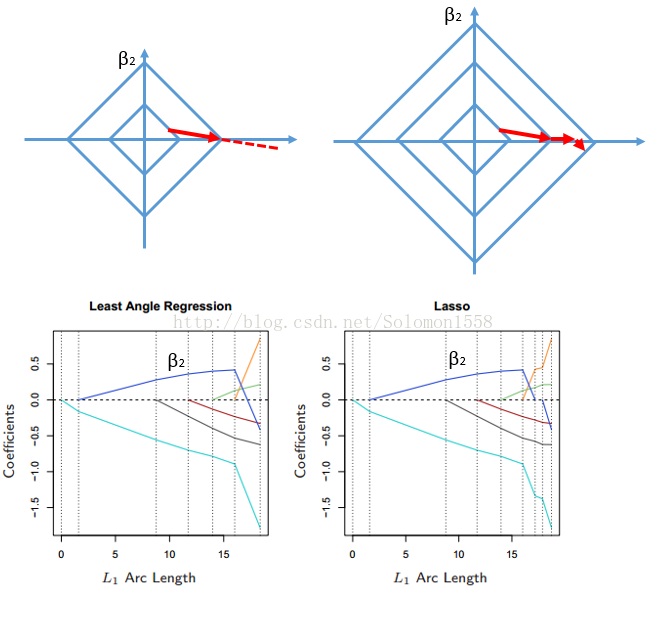
Lasso estimate的提出是Tibshirani在1996年JRSSB上的一篇文章Regressionshrinkage and selection via lasso。所谓lasso，其全称是least absolute shrinkage and selection operator。其想法可以用如下的最优化问题来表述：

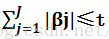
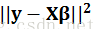
在限制了的情况下，求使得残差平方达到最小的回归系数的估值。

Lasso estimate具有shrinkage和selection两种功能。关于selection功能，Tibshirani提出，当t值小到一定程度的时候，lasso estimate会使得某些回归系数的估值是0，这确实是起到了变量选择的作用。当t不断增大时，选入回归模型的变量会逐渐增多，当t增大到某个值时，所有变量都入选了回归模型，这个时候得到的回归模型的系数是通常意义下的最小二乘估计。从这个角度上来看，lasso也可以看做是一种逐步回归的过程。

5. 用LARS求解Lasso回归

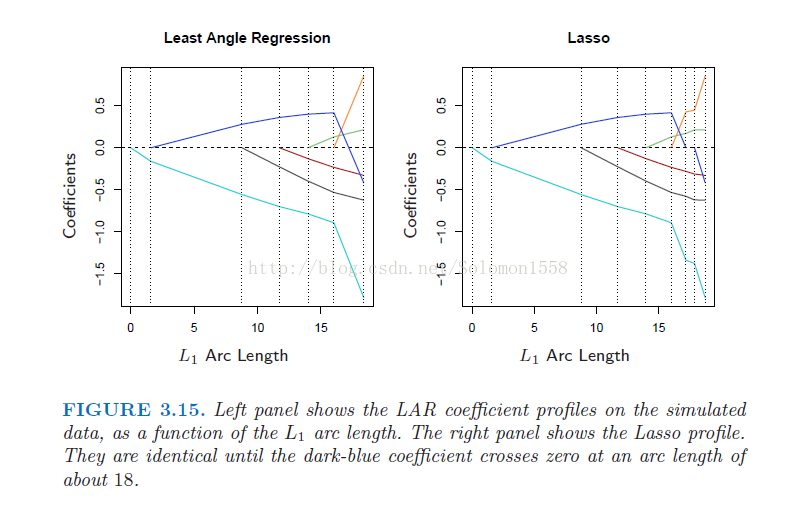
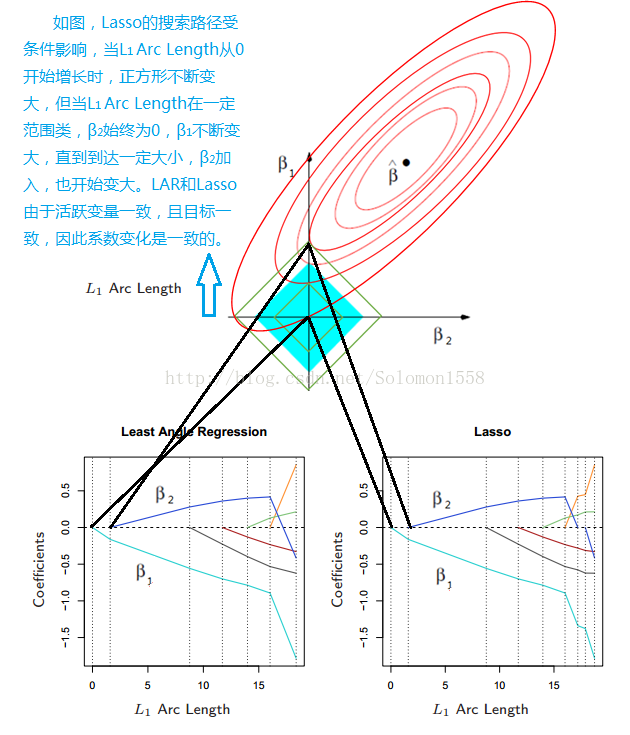
如下图显示LAR和Lasso的轨迹图十分相似，它们选取变量一致，都以最小二乘为目的方向，系数也一致。

5.1 从几何角度解释二者相似的原因：

5.2 两者的差异

两者的差异在于LAR没有考虑Lasso的限制条件：

因此在当系数穿越0时会超出条件，LAR不理会限制条件会继续沿着路径前进，而Lasso会顾虑限制条件，改变方向，从而在L1继续增大时β2暂时仍为0，直至条件允许。

6. 一种修正的LARS算法

Efron提出了一种修正的LARS算法，可以用修正的LARS算法来求解所有的lasso estimates。下面我介绍一下这种修正的LARS算法。

首先假设我们已经完成了几步LARS steps。这时候，我们已经有了一个回归变量集，我们记这个回归变量集为XA。这个集合就对应着一个对于Y的估计，我们记为μ^A。这个估值对应着一个lasso方法对于响应的估值（这里我认为LARS估值和lasso估值应该是一样的），lasso的估值，对应着回归系数的lasso估值，回归系数向量的lasso估值我们记为β^。

为了继续进行下一步，我们先给出一个向量的表达式，然后再解释一下它

XAwA就是LARS算法的在当前回归变量集下的solution path。那么我们可以把wA作为β的proceed的path。Efron定义了一个向量d^,这个向量的元素是sjwj,其中sj是入选变量xj与当前残差的相关系数的符号，也是βj^的符号。对于没有入选的变量，他们对应在d^中的元素为0。也就是对应着μ(r)=Xβ(r)，我们有

将LARS的solution path对应到lasso estimate的path上，这种对应的想法非常值得借鉴。

很显然，βj(r)会在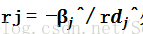处变号。那么对于我们已经有的lasso estimateβ(r),它中的元素会在最小的的那个大于0的rj处变号。我们记之为r¯。如果没有rj大于0,那么r¯就记为无穷大。

对于LARS本身而言，在已经有了如今的回归变量集和当前残差的基础上，我们就会有条solution path，在这个solution path上proceed的最大步记为r^.通过比较r^和r¯就会有进一步的想法。Efron的文章证明了如果r¯小于r^，则对应于LARS估计的那个βj(r)不会成为一个lasso estimation。（这个是因为当前残差和对应变量的相关系数的符号一定是和该变量的系数符号一致才行）。在这种情况下，我们就不能继续在LARS的solution path上继续前进了，为了利用LARS算法求得lasso estimate，Efron提出把r¯所对应的那个rj所对应的xj从回归变量中去掉。去掉之后再计算当前残差和当前这些变量集之间的相关系数，从而确定一条新的solution path，继续进行LARS step。这样进行下去，可以通过LARS算法得到所有的lasso estimate。

这个对于LARS的lasso修正算法，被Efron称作“one at a time”条件，也就是每一步都要增加或删掉一个变量。下图显示了用修正了的LARS算法求lasso estimate的过程。