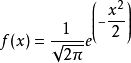正态分布
对于正态分布,首先补充其理论知识,然后我们根据<深入浅出统计学>中的计算步骤,进行编程实现.
正态分布(Normal distribution),也称“常态分布”,又名高斯分布(Gaussian distribution),最早由A.棣莫弗在求二项分布的渐近公式中得到。C.F.高斯在研究测量误差时从另一个角度导出了它。P.S.拉普拉斯和高斯研究了它的性质。是一个在数学、物理及工程等领域都非常重要的概率分布,在统计学的许多方面有着重大的影响力。
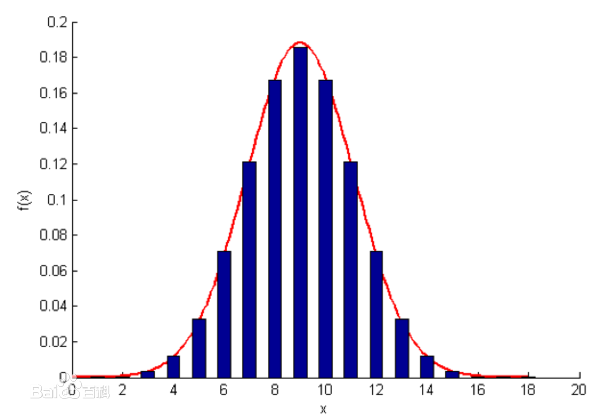
正态曲线呈钟型,两头低,中间高,左右对称因其曲线呈钟形,因此人们又经常称之为钟形曲线。
若随机变量X服从一个数学期望为μ、方差为σ^2的正态分布,记为N(μ,σ^2)。其概率密度函数为正态分布的期望值μ决定了其位置,其标准差σ决定了分布的幅度。当μ = 0,σ = 1时的正态分布是标准正态分布。
定理
由于一般的正态总体其图像不一定关于y轴对称,对于任一正态总体,其取值小于x的概率。只要会用它求正态总体在某个特定区间的概率即可。
为了便于描述和应用,常将正态变量作数据转换。将一般正态分布转化成标准正态分布。
若
服从标准正态分布,通过查标准正态分布表就可以直接计算出原正态分布的概率值。故该变换被称为标准化变换。(标准正态分布表:标准正态分布表中列出了标准正态曲线下从-∞到X(当前值)范围内的面积比例。)
标准正态分布
当 时,正态分布就成为标准正态分布
分布曲线的图形特征
集中性:正态曲线的高峰位于正中央,即均数所在的位置。
对称性:正态曲线以均数为中心,左右对称,曲线两端永远不与横轴相交。
均匀变动性:正态曲线由均数所在处开始,分别向左右两侧逐渐均匀下降。
曲线与横轴间的面积总等于1,相当于概率密度函数的函数从正无穷到负无穷积分的概率为1。即频率的总和为100%。
关于μ对称,并在μ处取最大值,在正(负)无穷远处取值为0,在μ±σ处有拐点,形状呈现中间高两边低,正态分布的概率密度函数曲线呈钟形,因此人们又经常称之为钟形曲线。
正态概率计算三步走
- 确定分布与范围
如果正态分布适用于遇到的情况,则看看是否能求出均值和标准差.只要先得知这些信息,才能求出概率;还需要弄清楚要求的是哪一部分面积 - 数据标准化
使数据标准化,从而得到一个标准正态曲线.下面我会给出相应的代码. - 查找概率
在原书中所写的是在概率表中直接查找相应的概率,但是在这里我们只需要编程求得即可,不再需要这么麻烦的操作.
例题与代码
能不能找到心上人-朱莉的相亲问题
问: 朱莉有一个问题,她希望理想中的伴侣能够比她高,最好能够比穿上五英寸高跟鞋的她还要高,这样她就可以自在的穿高跟鞋了。我们查找数据,统计邦的男生身高服从于N(71,20.25),而朱莉身高64英寸,那么在穿和不穿高跟鞋的两种情况下,朱莉的约会者比她高的概率是多少呢?
答: 此处我们使用scipy.stats中的norm类解决该问题,在默认情况下norm为X~N(0,1)的标准正态分布,如果有需要的话,比如我们想要直接计算X~N(3,4^2)的正态分布,我们也可以使用norm_34=norm(3,4)类似的语法来创建我们需要的norm类,要注意的是前面的3 为 期望μ,而方差σ = 4 。
from scipy.stats import norm
# 对于不服从标准正态分布的函数我们需要先进行标准化,也就是Z = (X - μ) / σ
# math.sqrt(20.25) = 4.5
print("约会者比朱莉高的概率为:{0:.3f}".format(1 - norm.cdf((64-71)/4.5)))
print("约会者比穿五英寸高根鞋的朱莉高的概率为:{0:.3f}".format(1 - norm.cdf((69-71)/4.5)))约会者比朱莉高的概率为:0.940
约会者比穿五英寸高根鞋的朱莉高的概率为:0.672
看来我们的朱莉能够很快找到符合择偶标准的心上人的,既然如此,我们还是回到语法上来,更加深入的学习一下语法问题吧.更多语法问题请参考scipy的norm 模块,不过鉴于我们不需要知道这么多,所以列出常用函数如下:
# 计算负无穷到x的概率
print(norm.cdf(-0.15))
# 计算负无穷到点的概率
print(norm.cdf([-0.15,0.5]))
print(norm.cdf([-0.15,0.15]))
# 概率密度函数
print(norm.pdf(0.15))0.4403823076297575
[0.44038231 0.69146246]
[0.44038231 0.55961769]
0.39447933090788895
爱情就像过山车-不止一个事件
最近婚礼筹办市场办的红火,德克推出了”爱情过山车”项目,可是过山车载重超过380磅就会有危险.我们的新郎和新娘还能顺利的坐上过山车吗?
对于之前朱莉的相亲问题,她的相亲对象只有一个,因此我们只要计算一个独立事件的正态分布就可以了.但是现在我们要计算的是新郎和新娘两个人体重的正态分布,来确保他们的综合体重不超过380磅,这个时候又要这么办呢?
对于计算两个事件的综合概率,我们首先要搞清楚的是这两个事件是否独立,然后要计算的概率分布类型.首先对于新郎和新娘的体重这两个事件而言,应该属于两个独立事件.我们需要按照两个独立变量去求解.而综合体重也属于连续数据,而且也是符合正态分布的.那么我们要求解的就是两个独立变量的综合正态分布.对于两个独立事件的正态分布,其期望与方差的计算方式与之前四五章的离散概率的计算是一样的
E(X+Y) = E(X)+E(Y)
E(X-Y) = E(X)-E(Y)
Var(X+Y) = Var(X)+Var(Y)
Var(X-Y) = Var(X)+Var(Y)现在已知新郎的体重:Y~N(190,500),新娘体重:X~N(150,400),那么两者综合体重小于380的概率为:
根据上面的双独立变量的期望与方差计算,已知新郎和新娘两人体重的正态分布,那么可以得到,两人综合体重的正态分布为 (X+Y)~N(340,900),由代码计算得到:
import math
print("第一种计算方式先化为标准分,然后计算",norm.cdf((380-340)/math.sqrt(900)))
print("第二种计算方式:直接声明一个(X+Y)~N(340,900)的norm类")
norm_340_30 = norm(340,30)
print(norm_340_30.cdf(380))第一种计算方式先化为标准分,然后计算 0.9087887802741321
第二种计算方式:直接声明一个(X+Y)~N(340,900)的norm类
0.9087887802741321
替代计算
泊松分布与正态分布
当二项分布的n很大而p很小时,泊松分布可作为二项分布的近似,其中λ为np。通常当n≧20,p≦0.05时,就可以用泊松公式近似得计算。
事实上,泊松分布正是由二项分布推导而来的,具体推导过程可参见百度百科-泊松分布词条相关部分。其对应关系如下:
X ~ Po(λ)
X ~ N(λ ,λ)
μ = λ = σ^2二项分布与正态分布
仅仅从数学角度上来讲,当np,nq双双大于 5 时,二项分布也可以通过近似正态分布来计算。但是因为两者一个为连续性分布,一个为离散型分布,所以必须要进行连续性修正。
划分方式十分简单,当需要计算二项分布的整数时,只需要计算该整数上下0.5的连续变量即可。换句话也就数说,正态分布中[n-0.5,n+0.5]这一连续区间的概率即为 二项分布中 n这一整数所对应的概率。
踏破铁鞋无觅处-只因没有计算机?
对于编程计算的我们而言,使用正态分布近似来简化二项分布的计算其实已经是一种得不偿失的方法。对于计算机而言,即使很大的正态分布也可以在一秒钟之内算完。不过这并不代表着我们就不需要了解正态分布近似二项分布这一数学性质了。所以即使是已经有计算机,不再需要简化运算,而更求精度与编写效率的我们,基本数学知识也是必不可少的。
参考
[1] 百度百科-正态分布
[2] scipy的norm 模块
[3] 《深入浅出统计学》