cf Educational Codeforces Round 47 E. Intercity Travelling

原题：
E. Intercity Travelling
time limit per test1.5 seconds
memory limit per test256 megabytes
inputstandard input
outputstandard output
Leha is planning his journey from Moscow to Saratov. He hates trains, so he has decided to get from one city to another by car.

The path from Moscow to Saratov can be represented as a straight line (well, it’s not that straight in reality, but in this problem we will consider it to be straight), and the distance between Moscow and Saratov is n km. Let’s say that Moscow is situated at the point with coordinate 0 km, and Saratov — at coordinate n km.

Driving for a long time may be really difficult. Formally, if Leha has already covered i kilometers since he stopped to have a rest, he considers the difficulty of covering (i+1)-th kilometer as ai+1. It is guaranteed that for every i∈[1,n−1] ai≤ai+1
. The difficulty of the journey is denoted as the sum of difficulties of each kilometer in the journey.

Fortunately, there may be some rest sites between Moscow and Saratov. Every integer point from 1 to n−1 may contain a rest site. When Leha enters a rest site, he may have a rest, and the next kilometer will have difficulty a1, the kilometer after it — difficulty a2, and so on.

For example, if
n=5 and there is a rest site in coordinate 2, the difficulty of journey will be 2a1+2a2+a3: the first kilometer will have difficulty a1, the second one — a2, then Leha will have a rest, and the third kilometer will have difficulty a1, the fourth — a2, and the last one — a3. Another example: if n=7 and there are rest sites in coordinates 1 and 5, the difficulty of Leha’s journey is 3a1+2a2+a3+a4.

Leha doesn’t know which integer points contain rest sites. So he has to consider every possible situation. Obviously, there are
2^(n−1) different distributions of rest sites (two distributions are different if there exists some point x such that it contains a rest site in exactly one of these distributions). Leha considers all these distributions to be equiprobable. He wants to calculate p — the expected value of difficulty of his journey.

Obviously,
p⋅2^(n−1) is an integer number. You have to calculate it modulo 998244353.
Input
The first line contains one number n (1≤n≤10^6) — the distance from Moscow to Saratov.The second line contains n integer numbers a1, a2, …, an (1≤a1≤a2≤⋯≤an≤10^6), where ai is the difficulty of i-th kilometer after Leha has rested.

Output
Print one number — p⋅2^(n−1), taken modulo 998244353.

Examples
input
2
1 2
output
5
input
4
1 3 3 7
output
60

中文：

有一个人旅行，从一个一维数轴上，从0点走到n点，给你n个数 $a_i$ ，表示这个旅行者连续走了x个点后的疲劳程度，例如：
如果他连续走了两个点，那么疲劳程度就是 $a_1+a_2$ ，如果连续走了n个点，疲劳程度就是 $a_1+a_2+a_3+...+a_n$ ，在[1,n-1]这些点上，每个都有相同的可能存在一个休息站，从休息站出发后，他的疲劳值从头计算，例如：在第3个点上有一个休息站，那么他走到n点的疲劳值总和就是 $a_1+a_2+a_3+a_1+a_2+...a_{n-3}$ ，现在问你这个人从起点走到终点的疲劳值的期望值是多少？期望值结果乘以 $2^{(n-1)}$ ，再对998244353取余数。

扫描二维码关注公众号，回复： 3037966 查看本文章

代码：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll maxn=1000001;
const ll mod=998244353;

ll pow_2[maxn];
ll a[maxn];
int n;

int main()
{
    ios::sync_with_stdio(false);
    while(cin>>n)
    {
        for(int i=1;i<=n;i++)
            cin>>a[i];
        pow_2[0]=1;
        for(int i=1;i<=n;i++)
            pow_2[i]=(pow_2[i-1]*2)%mod;

        ll ans=pow_2[n-1]*a[1]%mod,pre=a[1];

        for(int i=2;i<=n;i++)
        {
            ans+=(pow_2[n-i]*a[i]%mod+pow_2[n-i]*pre%mod)%mod;
            pre=(pre*2%mod+a[i]%mod)%mod;
        }
        cout<<ans%mod<<endl;
    }

    return 0;
}

思路：

有[1,n-1]个点，每个点有等可能性出现休息站，那么每个点出现休息站的可能性都是 $1/2$ 。

考虑有n个点，连续的疲劳值是 $a_1$ 一直到 $a_n$ 。

那么每个点出现休息站与不出现休息

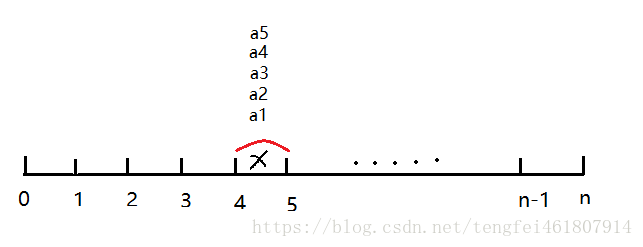
如图
这里写图片描述

考虑第x段分别为a1,a2,a3,a4,a5的方案数是多少？设为 $x_1,x_2,x_3,x_4,x_5$

$x_1=2^3·2^{n-5}$ 种可能性，前面的 $2^3$ 表示点4肯定是休息站，点1，2，3分别是或不是休息站的方案一共有 $2^3$ 种，再乘以点5后面的每个点是或不是休息点的方案数一共有 $2^{n-5}$ 种。所以，在x段 $a_1$ 出现的次数是 $x_1$ 。

同理，计算 $x_2=2^2·2^{n-5}$ ，表示点4肯定不能是休息站，点3必须是休息站，前面的点2和点1是或不是休息站会造成 $2^2$ 种可能，再乘以后面 $2^{n-5}$ 种可能，则在x段出现 $a_2$ 的次数是 $x_2$ 种可能。

一直计算到 $x_5$ ，就能把第x段出现的所有可能枚举全，而且不重复，不遗漏。

由于最后的期望值是乘以 $2^{n-1}$ ，那么就把所有的分数都约掉了，即概率 $(1/2)^{n-1}$

那么，推广到n，在第i段，最长只可以出现 $a_i$ ，即只有前i-1个点中，没有任何休息站。

[0,1]出现a1的方案数为 $2^{n-1}·a_1$
[1,2]出现a1与a2的方案数为 $2^{n-2}·(a_2+a_1)$
[2,3]出现a1,a2,a3的方案数为 $2^{n-3}·(a_3+a_2+2a_1）$
[3,4]出现a1,a2,a3,a4的方案数为 $2^{n-4}·(a_4+a_3+2a_2+2^2a_1)$
[4,5]出现a1,a2,a3,a4,a5的方案数为 $2^{n-5}·(a_5+a_4+2a_3+2^2a_2+2^3a_1)$
….
一直计算到区间[n-1，n]累加即为答案

上面的计算公式中，可以看出在括号中的式子存在递推的规律可以在线性时间中算出，见代码。

对于区间的组合问题，考虑每个区间段的情况是一种很好的枚举方式，这样可以避免重复或者遗漏的情况发生。

cf Educational Codeforces Round 47 E. Intercity Travelling

猜你喜欢