[BZOJ4754][Jsoi2016]独特的树叶（树Hash+树形DP+换根）

Address

https://www.lydsy.com/JudgeOnline/problem.php?id=4754

Solution

先介绍一下有根树的哈希：
（1）一个节点的树，哈希值为 $1$ 。
（2）设 $f[u]$ 为 $u$ 的子树的哈希值。先将 $u$ 的所有子节点按照子树哈希值从小到大排序，取底数 $W$ 和模数 $P$ ，设 $v_i$ 是 $u$ 的第 $i$ 个（满足 $f[v_i]$ 是 $u$ 的所有子节点的 $f$ 中第 $i$ 小的），那么可以用树形 DP 求得 $f[u]$ ：

$$f[u]=(u的子树大小)\times\sum_{i=1}^{u的子节点数}f[v_i]\times W^{i-1}\bmod P$$
树哈希有一个重要应用：判断两棵树是否同构。
两棵无根树同构的概念：两棵无根树同构，当且仅当将其中一棵树的节点编号重排之后，所有的边能够与另一棵树所有的边一一对应。同样地，我们也能引入有根树同构的概念：将一棵树的节点编号重排，如果根节点 $u$ 的编号变成了 $w$ ，另一棵树的根为 $v$ ，那么这两棵有根树同构，当且仅当重排后第一棵树在以 $w$ 为根时各个点的父子关系与第二颗树在以 $v$ 为根时各个点的父子关系相同。
判断同构方法：
两棵无根树同构，当且仅当存在第一棵树的节点 $u$ 和第二棵树的节点 $v$ 满足第一棵树以 $u$ 为根的哈希值和第二棵树以 $v$ 为根的哈希值相等，即第一棵树以 $u$ 为根和第二棵树以 $v$ 为根形成的两棵有根树同构。
（两棵有根树同构，当且仅当第一棵树的根 $u$ 和第二棵树的根 $v$ 的度数相等，并且 $u$ 的子节点能够经过重排使得对于每个（ $1\le i\le u的度数$ ）都满足 $u$ 的第 $i$ 个子节点的子树与 $v$ 的第 $i$ 个子节点的子树同构。通过 DP 式即可证明判断同构的方法。）
现在回到原问题。
考虑求出 $A$ 和 $B$ 两棵树以每个节点为根的哈希值。
$A$ 和 $B$ 的求法相同，故下面只对 $A$ 进行讨论。
先强制以 $1$ 为根，求 $f[u]$ 表示 $u$ 子树的哈希值。
如果求出每个节点为根的哈希值，那么暴力枚举根是 $O(n^2\log n)$ （排序带有一个 $\log n$ ）的，显然过不去。
故我们考虑换根树形 DP 。
设 $g[u]$ 表示 $A$ 整棵树将 $u$ 及 $u$ 的子树内的所有点去掉之后，剩下的 $n-size[u]$ （ $size[u]$ 为 $u$ 的子树大小）个点构成的树，以原树上 $u$ 的父亲为根的树的哈希值。
用一张图片可以这样描述：

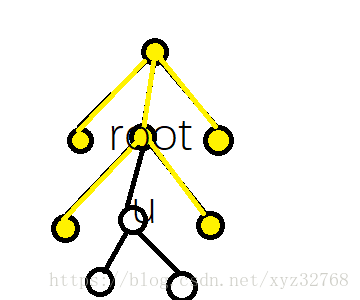
上图中，黄色的节点和边表示 $g[u]$ 表示的连通子树， $g[u]$ 就表示这棵连通子树以 $root$ 为根的哈希值。
考虑对于一个 $u$ ，求出 $u$ 的所有子节点的 $v$ 值。
首先把 $g[u]$ （如果 $u$ 不为 $1$ ）和所有子节点的 $f$ 值（子节点v除外）存进一个数组 $val$ ，将 $val$ 从小到大排序，那么容易得到 $g[v]$ 的转移（ $m$ 为 $val$ 数组的元素个数）：
$$g[v]=(n-size[v])\times\sum_{i=1}^mval[i]\times W^{i-1}\bmod P$$
如果除了 $1$ 之外所有的点都与 $1$ 有边直接相连，那么这样复杂度仍然是 $O(n^2\log n)$ 。
考虑对于每个 $u$ ，事先将所有子节点 $v$ 生成一个二元组 $(v,f[v])$ 存进数组 $val$ ，然后如果 $u$ 不为 $1$ 就将二元组 $(-1,g[u])$ 存进数组 $val$ ，然后将 $val$ 数组以第二个元素为关键字从小到大排序。
为了实现 $g$ 的 $O(1)$ 转移，考虑记录前缀后缀和（ $vf(i)$ 表示 $val$ 数组第 $i$ 个数的第二个元素）：
$$pre[i]=(pre[i-1]+vf(i)\times W^{i-1})\bmod P$$
$$suf[i]=(suf[i+1]+vf(i)\times W^{i-2})\bmod P$$
这样，我们就能实现了 $O(1)$ 的转移。
对于 $u$ 的子节点 $v$ ，如果 $val$ 第 $i$ 个数的第一个元素为 $v$ ，那么有：
$$g[v]=(n-size[v])\times(pre[i-1]+suf[i+1])\bmod P$$
注意：如果 $1$ 号节点的度数为 $1$ ，那么要把 $g[1]$ 设为 $1$ 而不是 $0$ 。
利用和求 $g$ 类似的方法，我们可以通过 $g[u]$ 和 $f[v]$ （ $v$ 为 $u$ 的子节点）求得 $res[u]$ 表示以 $u$ 为根的哈希值。求 $res$ 时，就不需要去掉 $u$ 的子树的影响，故不需要使用 $pre$ 和 $suf$ 。
对 $A$ 树和 $B$ 树都进行了一遍 DP 后，就可以求解了！
先把 $A$ 树的所有节点的 $res$ 存进一个 map 中。
多余的节点一定是 $B$ 中度数为 $1$ 的节点。
由哈希函数得到，对于 $B$ 中一个度数为 $1$ 的节点 $u$ ，如果存在边 $(u,v)$ ，那么去掉 $u$ 之后 $B$ 以 $v$ 为根的哈希值为 $\frac{res[u]}{n+1}$ 。（模数 $P$ 为质数时，利用逆元可以求出这个值）
而这时候只需要判断 $A$ 树中是否有一个 $res$ 等于上式即可。
在 map 中查询，就能快速地判断。
复杂度 $O(n\log n)$ 。

Code

#include <map>
#include <cmath>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#define For(i, a, b) for (i = a; i <= b; i++)
#define Rof(i, a, b) for (i = a; i >= b; i--)
#define Tree(u) for (int e = adj[u], v; e; e = nxt[e]) if ((v = go[e]) != fu)
using namespace std;
inline int read() {
    int res = 0; bool bo = 0; char c;
    while (((c = getchar()) < '0' || c > '9') && c != '-');
    if (c == '-') bo = 1; else res = c - 48;
    while ((c = getchar()) >= '0' && c <= '9')
        res = (res << 3) + (res << 1) + (c - 48);
    return bo ? ~res + 1 : res;
}
const int N = 1e5 + 10, M = N << 1, Z = 239, ZZQ = 1e9 + 9;
int n, tot, val[N], pre[N], suf[N], pw[N];
map<int, int> chs;
struct cyx {
    int u, f;
} lav[N];
inline bool comp(const cyx &a, const cyx &b) {
    return a.f < b.f;
}
int qpow(int a, int b) {
    int res = 1;
    while (b) {
        if (b & 1) res = 1ll * res * a % ZZQ;
        a = 1ll * a * a % ZZQ;
        b >>= 1;
    }
    return res;
}
struct Tree {
    int n, ecnt, nxt[M], adj[N], go[M], f[N], g[N], ans[N], sze[N], cnt[N];
    void clean(int _n) {
        int i;
        ecnt = 0; n = _n;
        For (i, 1, n) adj[i] = f[i] = g[i] = ans[i] = 0;
    }
    void add_edge(int u, int v) {
        nxt[++ecnt] = adj[u]; adj[u] = ecnt; go[ecnt] = v;
        nxt[++ecnt] = adj[v]; adj[v] = ecnt; go[ecnt] = u;
        cnt[u]++; cnt[v]++;
    }
    void dpfirst(int u, int fu) {
        sze[u] = 1;
        Tree(u) dpfirst(v, u), sze[u] += sze[v];
        int i, bas = 1;
        tot = 0;
        Tree(u) val[++tot] = f[v];
        f[u] = 0;
        sort(val + 1, val + tot + 1);
        For (i, 1, tot)
            f[u] = (f[u] + 1ll * val[i] * bas % ZZQ) % ZZQ,
            bas = 1ll * bas * Z % ZZQ;
        f[u] = 1ll * f[u] * sze[u] % ZZQ;
        if (!tot) f[u] = 1;
    }
    void dplast(int u, int fu) {
        int i, bas = 1;
        tot = 0;
        Tree(u) lav[++tot] = (cyx) {v, f[v]};
        if (fu) lav[++tot] = (cyx) {-1, g[u]};
        sort(lav + 1, lav + tot + 1, comp);
        pw[0] = 1; pre[0] = suf[tot + 1] = 0;
        For (i, 1, tot) pw[i] = 1ll * pw[i - 1] * Z % ZZQ;
        For (i, 1, tot - 1) pre[i] =
            (pre[i - 1] + 1ll * lav[i].f * pw[i - 1] % ZZQ) % ZZQ;
        Rof (i, tot, 2) suf[i] =
            (suf[i + 1] + 1ll * lav[i].f * pw[i - 2] % ZZQ) % ZZQ;
        For (i, 1, tot) {
            if (lav[i].u == -1) continue;
            g[lav[i].u] = 1ll * (n - sze[lav[i].u]) *
                (pre[i - 1] + suf[i + 1]) % ZZQ;
        }
        if (!fu && tot == 1) g[lav[1].u] = 1;
        For (i, 1, tot) ans[u] = (ans[u] + 1ll * lav[i].f * bas % ZZQ) % ZZQ,
            bas = 1ll * bas * Z % ZZQ;
        ans[u] = 1ll * ans[u] * n % ZZQ;
        Tree(u) dplast(v, u);
    }
} T1, T2;
int main() {
    int i, x, y;
    n = read();
    T1.clean(n); T2.clean(n + 1);
    For (i, 1, n - 1) x = read(), y = read(),
        T1.add_edge(x, y);
    For (i, 1, n) x = read(), y = read(),
        T2.add_edge(x, y);
    T1.dpfirst(1, 0); T1.dplast(1, 0);
    T2.dpfirst(1, 0); T2.dplast(1, 0);
    For (i, 1, n) chs[T1.ans[i]] = 1;
    For (i, 1, n + 1) {
        if (T2.cnt[i] > 1) continue;
        if (chs[1ll * T2.ans[i] * qpow(n + 1, ZZQ - 2) % ZZQ])
            return printf("%d\n", i), 0;
    }
    return 0;
}