求1-N中每个数的正约数集合
我们开一个vector,把每个数的约数往后面压
vector<int> factor[500010];同时,i*j的一个约数一定有i
所以
for(int i=1;i<=n;i++)
for(int j=1;j<=n/i;j++)
factor[i*j].push_back(i)i=2,j=1,2,3,4,5,6,7
i=3,j=1,2,3,4...
i=4,j=1,2,3
i=5,j=1,2
...以此类推
| 1 | |
| 2 | 2 |
| 3 | 3 |
| 4 | 2,4 |
| 5 | 5 |
| 6 | 2,3 |
| 7 | |
| 8 | 2,4 |
| 9 | 3 |
| 10 | 2,5 |
| 11 | |
| 12 | 2,3,4 |
| 13 | |
| 14 | 2 |
| .... |
输出
for(int i=1;i<=n;i++){
for(int j=0;j<factor[i].size();j++)
cout<<factor[i][j]<<" ";
cout<<endl;
}最大公约数
欧几里得算法
gcd(a,b)=gcd(b,a%b)
证明
当a<b时 gcd(b,a%b)=gcd(b,a)=gcd(a,b)
当a>=b时 设a=qb+r gcd(b,a%b)=gcd(b,r)=d
d|r且d|b 所以d|qb+r即d|a
a,b的公约数集合与 b,a%b相等,所以最大公约数也相等
于是
int gcd(int a,int b){
if(b==0) return a;
return gcd(b,a%b);
}欧拉函数
1-N中与N互质的数的个数被称为欧拉函数,记为(N)
φ(10)=10×(1-1/2)×(1-1/5)=4 (1 3 7 9)
φ(30)=30×(1-1/2)×(1-1/3)×(1-1/5)=8;
φ(49)=49×(1-1/7)=42;
证明
代码
int phi(int n){
int ans=n;
for(int i=2;i<=sqrt(n);i++)
if(n%i==0){//i是质因子
ans=ans/i*(i-1);
while(n%i==0) n/=i;//把这个质因子搞没
}
if(n>1) ans=ans/n*(n-1);//是质数
return ans;
}性质
原网址 https://www.cnblogs.com/handsomecui/p/4755455.html
欧拉函数的性质:
(1) p^k型欧拉函数:
若N是质数p(即N=p), φ(n)= φ(p)=p-p^(k-1)=p-1。
若N是质数p的k次幂(即N=p^k),φ(n)=p^k-p^(k-1)=(p-1)p^(k-1)。
(2)mn型欧拉函数
设n为正整数,以φ(n)表示不超过n且与n互素的正整数的个数,称为n的欧拉函数值。若m,n互质,φ(mn)=(m-1)(n-1)=φ(m)φ(n)。
一些补充的性质
若p|n且p^2|n 则
若p|n但p^2%n!=0,则
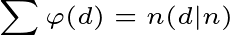
证明
n/p与n包涵相同的质因子
因为p^2%n!=0 所以n/p与p互质
例题
描述
如果从(0,0)到(x,y)的线,则从原点可见第一象限(x和y是大于或等于0的整数)中的格点(x,y),而不是原点 )不会通过任何其他格点。 例如,点(4,2)不可见,因为来自原点的线穿过(2,1)。 下图显示了点(x,y),其中0≤x,y≤5,从原点到可见点的线。
编写一个程序,给定大小值N,计算0≤x,y≤N的可见点数(x,y)。
输入
第一行输入包含一个整数C(1≤C≤1000),它是后面的数据集数。
每个数据集由一行输入组成,其中包含一个整数N(1≤N≤1000),即大小。
输出
对于每个数据集,应该有一行输出,包括:从1开始的数据集编号,单个空格,大小,单个空格以及该大小的可见点数。
样本输入
4
2
4
5
231
样本输出1 2 5
2 4 13
3 5 21
4 231 32549
我们发现只有gcd(x,y)=1时,才会被看见
因为当gcd(x,y)=d时
已经被 x/d,y/d挡住了
我们只需要考虑一半,另一半关于(0,0),(N,N)对称
除去(1,1),(0,1),(1,0)三个点
在这一半中,我们发现第i列连的钉子在(1--i-1)行
不就是欧拉函数吗
另外,我们可以用线性算法推出欧拉函数
因为
若p|n且p^2|n 则
若p|n但p^2%n!=0,则
在线性算法中,n只会被最小质因子p筛一次
我们就可以从推到
#include<bits/stdc++.h>
#define N 1005
using namespace std;
int p[N],prime[N],phi[N];//最小质因子 质数 欧拉函数
int c,n,cnt;
void init(){
for(int i=2;i<=1005;i++){
if(!p[i]){//是质数
p[i]=i,prime[++cnt]=i;
phi[i]=i-1;
}
for(int j=1;j<=cnt;j++){
if(prime[j]>p[i]||prime[j]*i>1005) break;
p[prime[j]*i]=prime[j];
phi[prime[j]*i]=phi[i]*(i%prime[j]?prime[j]-1:prime[j]);
}
}
}
int main()
{
init();
cin>>c;
for(int i=1;i<=c;i++){
cin>>n;
int ans=0;
for(int j=2;j<=n;j++)
ans+=phi[j];
cout<<i<<" "<<n<<" "<<ans*2+3<<endl;
}
} 
