采样率转换理论基础

离散信号重采样（采样率转换）通常有两种实现办法

1】一种是通过DA转换成模拟信号然后再通过AD重新对模拟信号进行采样

2】一种是通过插值的办法在对输入信号进行插值或者抽取的方式，完成纯数字域的采样率转换

本文主要记录第二种方法

首先看以下重构函数以及插值公式

$g(t)=\frac{\sin (\pi t/ T)}{\pi t/ T}$

$y(t)=\sum _{n=-\infty}^{\infty}x(nT)g(t-nT)$

取时间序列为步进为Ty，就可以得到一个重构函数序列的计算公式

$g(mT_{y})=\frac{\sin (m\pi T_{y}/T)}{m\pi T_{y}/T} \qquad m=0,1,2,3...$

将采样周期为Tx的输入x（nTx）序列与这个插值序列卷积，就得到了一个经过插值的序列y（mTy），插值后采样周期变为Ty，插值后输出序列的第m个元素记为以下形式：

$y(mT_{y})=\sum_{n=-\infty }^{\infty}x(nT_{x})g(mT_{y}-nT_{x})\qquad m=0,1,2,3,...$ 公式1

针对公式1，进行代码验证，代码如下

clc
clear all
close all

% 建立一个离散序列
Tx = 0.05;
T = (1:fix(1/Tx))*Tx;
x = sin(2*pi*T);
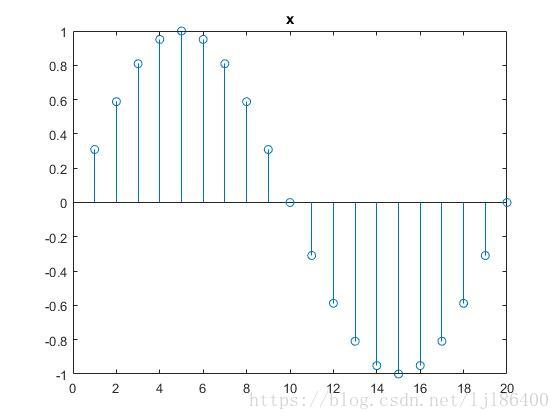
figure(1)
stem(x)
title('x')

% 验证插值函数
t = 0.002;                                   % 插值结果的分辨率，应该小于Tx,否则会出现混叠
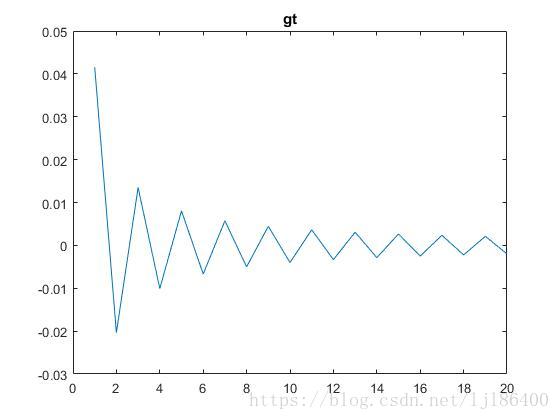
gt = sin(pi*(t-T)./Tx)./(pi*(t-T)./Tx);     % 插值函数产生的序列

figure
plot(gt)
title('gt')

% 查看整个插值后的序列
for tloop = 1:fix(1/t)
    
    tg = tloop * t;
    gt = sin(pi*(tg-T)./Tx)./(pi*(tg-T)./Tx);
    yt(tloop) = sum(x.*gt);
    
end
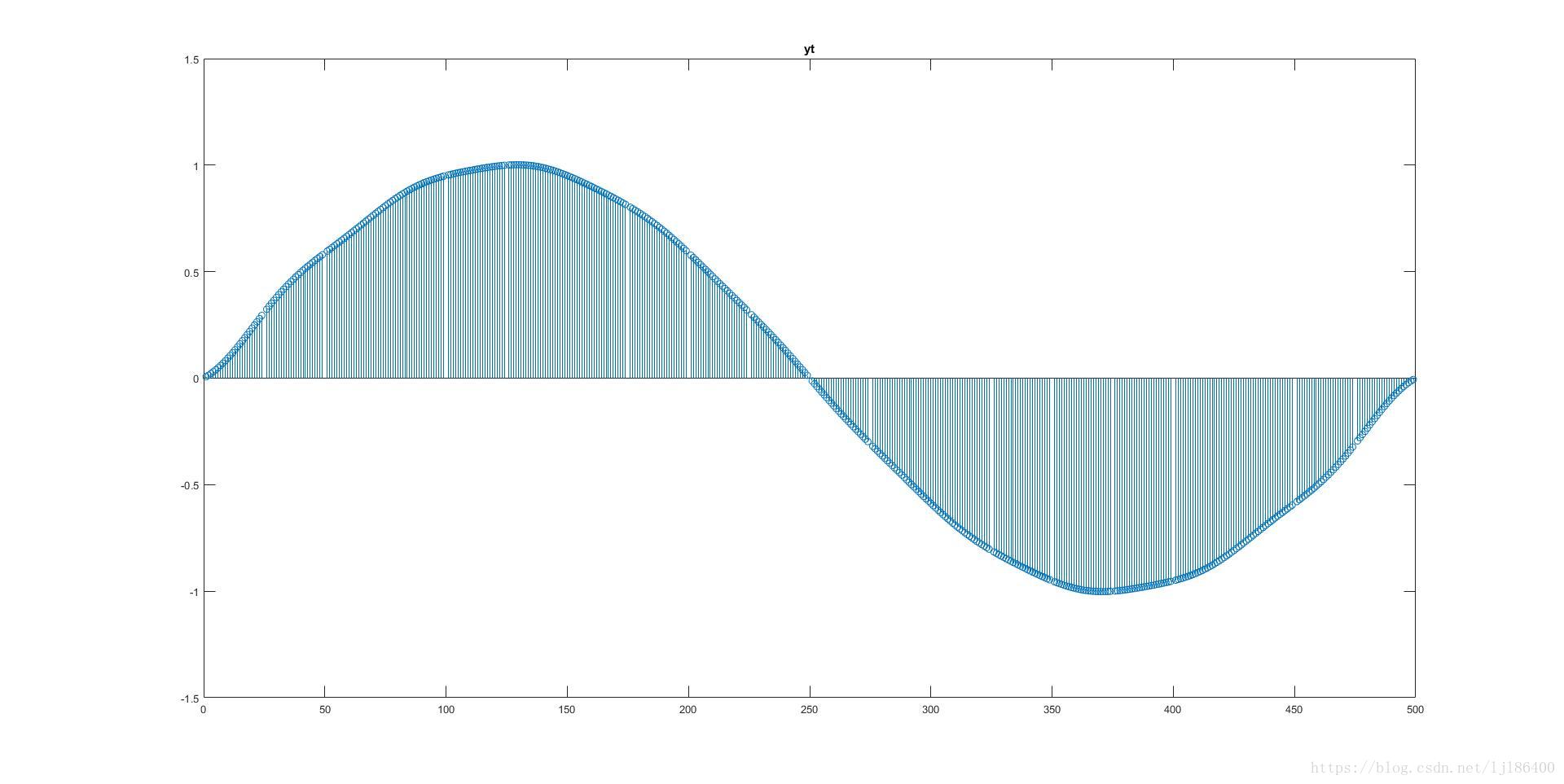
figure(3)
stem(yt)
title('yt')

验证结果