在网图和非网图中,最短路径的含义是不同的。网图是两顶点经过的边上权值之和最少的路径;非网图是两顶点之间经过的边数最少的路径。我们把路径起始的第一个顶点称为源点,最后一个顶点称为终点。关于最短路径的算法,我们会介绍两种:迪杰斯特拉算法(Dijkstra)与弗洛伊德算法(Floyd),具体例子如下图所示
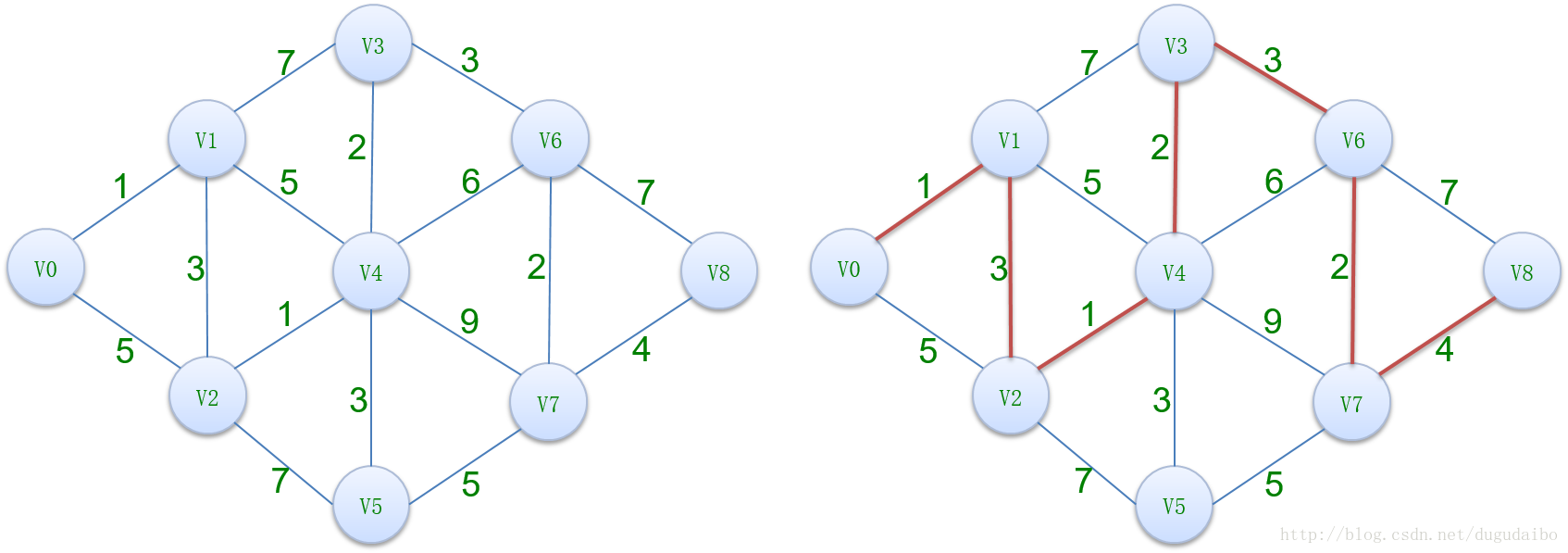
其中的图以邻接矩阵的方式进行存储,如下图所示

1. 迪杰斯特拉算法
迪杰斯特拉算法并不是一下子就求出了
1.1 代码
#define MAXVEX 9
#define INFINITY 65535 // 是 2^16 ,而不是 2^32,因为这样可以防止溢出
typedef int Patharc[MAXVEX]; // 用于存储最短路径下标的数组
typedef int ShortPathTable[MAXVEX]; // 用于存储到各点最短路径的权值和
void ShortestPath_Dijkstar(MGraph G, int V0, Patharc *P, ShortPathTable *D)
{
int v, w, k, min;
int final[MAXVEX]; // final[w] = 1 表示已经求得顶点V0到Vw的最短路径
// 初始化数据
for( v=0; v < G.numVertexes; v++ )
{
final[v] = 0; // 全部顶点初始化为未找到最短路径
(*D)[V] = G.arc[V0][v]; // 将与V0点有连线的顶点加上权值
(*P)[V] = 0; // 初始化路径数组P为0
}
(*D)[V0] = 0; // V0至V0的路径为0
final[V0] = 1; // V0至V0不需要求路径
// 开始主循环,每次求得V0到某个V顶点的最短路径
for( v=1; v < G.numVertexes; v++ )
{
min = INFINITY;
for( w=0; w < G.numVertexes; w++ )
{
if( !final[w] && (*D)[w]<min )
{
k = w;
min = (*D)[w];
}
}
final[k] = 1; // 将目前找到的最近的顶点置1
// 修正当前最短路径及距离
for( w=0; w < G.numVextexes; w++ )
{
// 如果经过v顶点的路径比现在这条路径的长度短的话,更新!
if( !final[w] && (min+G.arc[k][w] < (*D)[w]) )
{
(*D)[w] = min + G.arc[k][w]; // 修改当前路径长度
(*p)[w] = k; // 存放前驱顶点
}
}
}
}1.2 模拟执行代码
在上面的代码中,首先进行初始化操作,如下图所示

首先将 Final 数组元素全部置为 0 ,表示全部顶点初始化为未找到最短路径;因为这个时候还没有找到最短路径,所以下标 P 都是 0,同样标志位也都是 0。 V0至V0的路径为0,V0至V0不需要求路径,所以将第一个标志位标记为1。
然后开始主循环,每次求得 V0 到某个 V 顶点的最短路径。因为第一个顶点就是自己本身,没有路径所以循环从 1 开始,而不是从 0 开始。
当 v = 1时,进入第一个以结点下标为循环变量的 for 循环。当 w = 0时,!final[w] = 0,所以 if 循环是不会进入的,当 w = 1时,根据条件判断此时标志位为 0 且两顶点间存在边(即权值小于正无穷),所以可以进入 if 循环,记下这个时候结点的下标 k = 1,并将其所对应的权值作为临时的最小值储存起来;下一个顶点的边的权值没有 1 小,所以不进入 if ,之后都是无穷大,也不进入;至此第一个 for 循环结束,此时与 0 连接的最短路径的顶点为 1 且权值为 1,即min = (*D)[1] 。这时将下标为 1 的顶点的标志位置为 1,即final[1] = 1 ,如下图所示

进入第二个以结点下标为循环变量的 for 循环,它的主要作用是修正当前最短路径及距离,也就是说现在已经确定所有与 v0 构成的路径最短的是 v1 ,那么在已知这个前提下,判断 v0 到达剩下的点最短距离是多少。因为final[0] = final[1] = 1 ,所以从 w = 2 才开始有可能进入循环,min+G.arc[1][2] = 1 + 3 = 4 < (*D)[2] = 5,所以(*D)[2] = 4,(*P)[2] = 1;同理可以得到(*D)[3] = 8,(*P)[3] = 1;(*D)[4] = 6,(*P)[4] = 1;从 w = 5 开始不满足 if 的判断条件,所以后续都不会进入,至此 v=1 的情况循环执行完毕,如下图所示

已经可以确定的是,v0 到 v1 之间最短的路径是红色的那条,在已知这个的条件下,此时 v0 到达其他点的最短路径新增了黑色的三条,但是这三条是临时的,可能会在之后被其他的路径所替代,而红色的路径则是确定的,这时的数组及标志位如下图所示

当 v = 2时,进入第2个以结点下标为循环变量的 for 循环。在这个操作中可以得到k = 2,min = 4,final[2] = 1;同理进入第二个 for 循环,在这个循环中由于final[0] =final[1] =final[2] = 1,所以从 w = 3 开始执行循环。w= 3 的时候不满足 if 判断条件;w= 3 的时候,(*D)[4] = 5,(*P)[4] = 2;剩下的均不满足 if 判断条件;之后的循环都是这个样子的。
1.3 过程总结
在上面个的过程中实际上主要是两个过程,首先第一个过程是寻找出发点到某一个点的最短距离,这个是确定的,之后再从这个点出发,找到原点必经过改点到之后每一个点的最短路径;循环上面的过程直至走到终点。
2. 弗洛伊德算法
2.1 简单举例
以下面这个简单的图为例进行解释说明
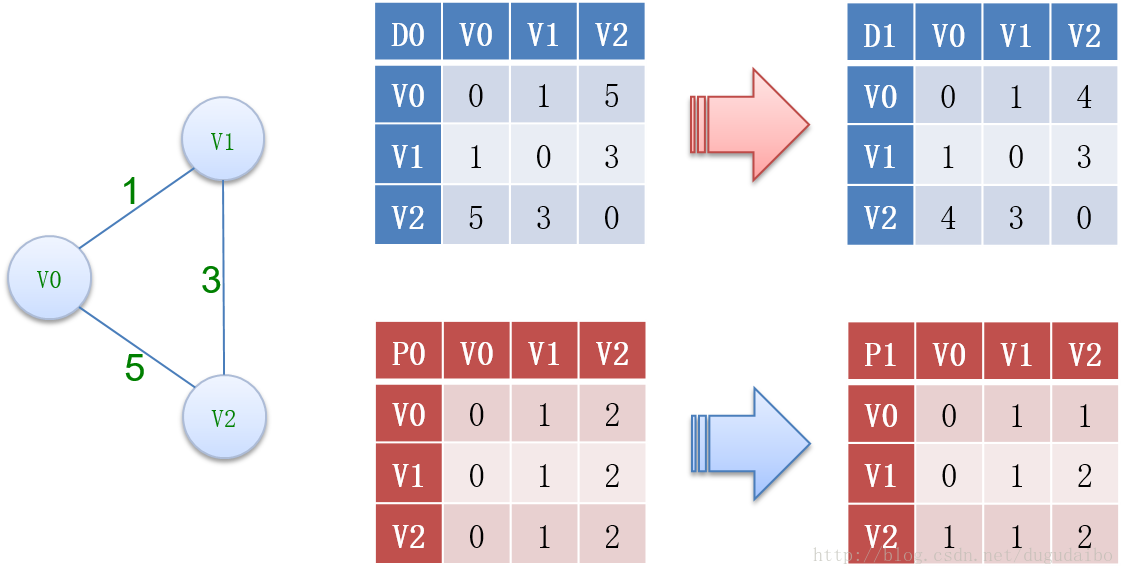
在上面这个例子中,D 表示最短路径,而 P0 表示以左面第一列的点为起始点,以上面第一行为终点的最短路径中,起始点的下一个点在哪里。第一列的两个矩阵表示初始情况,其中蓝色矩阵表示一个点到另一个点的最短路径初始化为该点直接到另一个点边的权值,如果边不存在就记为无穷大。而 P0 的初始化代表以左面第一列的点为起始点,以上面第一行为终点的最短路径中,都是从起始点直接一步走到终止点。
2.2 代码
#define MAXVEX 9
#define INFINITY 65535
typedef int Pathmatirx[MAXVEX][MAXVEX];
typedef int ShortPathTable[MAXVEX][MAXVEX];
void ShortestPath_Floyd(MGraph G, Pathmatirx *P, ShortPathTable *D)
{
int v, w, k;
// 初始化D和P
for( v=0; v < G.numVertexes; v++ )
{
for( w=0; w < G.numVertexes; w++ )
{
(*D)[v][w] = G.matirx[v][w]; //直接初始化为邻接矩阵
(*P)[v][w] = w; //初始化为这一列的值
}
}
// 优美的弗洛伊德算法
for( k=0; k < G.numVertexes; k++ )
{
for( v=0; v < G.numVertexes; v++ )
{
for( w=0; w < G.numVertexes; w++ )
{
if( (*D)[v][w] > (*D)[v][k] + (*D)[k][w] ) //判断目前最短路径中的
{
(*D)[v][w] = (*D)[v][k] + (*D)[k][w];
(*P)[v][w] = (*P)[v][k]; // 请思考:这里换成(*P)[k][w]可以吗?为什么?
}
}
}
}
}2.3 模拟代码执行
假设初始初始的连接矩阵如下所示
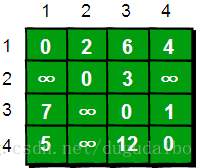
假如现在只允许经过1号顶点,求任意两点之间的最短路程,应该如何求呢?只需判断e[i][1]+e[1][j]是否比e[i][j]要小即可。e[i][j]表示的是从i号顶点到j号顶点之间的路程。e[i][1]+e[1][j]表示的是从i号顶点先到1号顶点,再从1号顶点到j号顶点的路程之和。其中i是1~n循环,j也是1~n循环,代码实现如下。
for(i=1;i<=n;i++)
{
for(j=1;j<=n;j++)
{
if ( e[i][j] > e[i][1]+e[1][j] )
e[i][j] = e[i][1]+e[1][j];
}
} 在只允许经过1号顶点的情况下,任意两点之间的最短路程更新为:
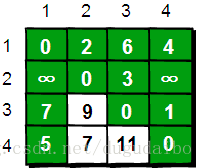
通过上图我们发现:在只通过1号顶点中转的情况下,3号顶点到2号顶点(e[3][2])、4号顶点到2号顶点(e[4][2])以及4号顶点到3号顶点(e[4][3])的路程都变短了。
接下来继续求在只允许经过1和2号两个顶点的情况下任意两点之间的最短路程。如何做呢?我们需要在只允许经过1号顶点时任意两点的最短路程的结果下,再判断如果经过2号顶点是否可以使得i号顶点到j号顶点之间的路程变得更短。即判断e[i][2]+e[2][j]是否比e[i][j]要小,代码实现为如下。
//经过1号顶点
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
if (e[i][j] > e[i][1]+e[1][j]) e[i][j]=e[i][1]+e[1][j];
//经过2号顶点
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
if (e[i][j] > e[i][2]+e[2][j]) e[i][j]=e[i][2]+e[2][j]; 在只允许经过1和2号顶点的情况下,任意两点之间的最短路程更新为:
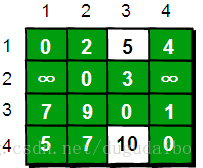
通过上图得知,在相比只允许通过1号顶点进行中转的情况下,这里允许通过1和2号顶点进行中转,使得e[1][3]和e[4][3]的路程变得更短了。
同理,继续在只允许经过1、2和3号顶点进行中转的情况下,求任意两点之间的最短路程。任意两点之间的最短路程更新为:
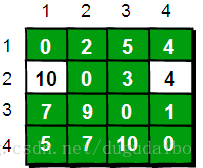
最后允许通过所有顶点作为中转,任意两点之间最终的最短路程为:
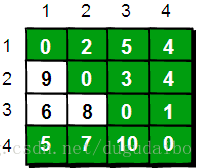
上面的过程实际上就是代码中执行弗洛伊德的部分,这段代码的基本思想就是:最开始只允许经过1号顶点进行中转,接下来只允许经过1和2号顶点进行中转……允许经过1~n号所有顶点进行中转,求任意两点之间的最短路程。用一句话概括就是:从i号顶点到j号顶点只经过前k号点的最短路程。
3. 算法比较
迪杰特斯拉算法的复杂度是
参考文献
[1]键盘里的青春, 《傻子也能看懂的弗洛伊德算法》,CSDN博客