之前学习了遗传算法对单目标函数的最优值求解,对于多目标问题。或者说是多目标函数的求解问题,我想再研究一下。正好,我也想改进一下之前的代码架构。不得不说,之前的代码是面向过程的架构,完全没有体现出python面向对象的特点。于是在上篇里更新了面向对象的程序。
一.举个多目标函数的简单例子
这里我们举个二元函数的最大值优化例子:
根据之前所学,
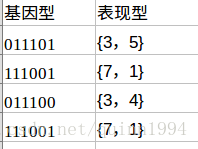
第一步,编码。这里我们采用二进制对个体基因型编码,将个体表现型编码为十进制。如,基因型x=100001对应的表现型是{4,1}。
第二步,初始生成种群。本例中,随机生成4个个体组成一个种群。如下,{011101}{101011}{011100}{111001},其表现型为{3,5}{5,3}{3,4}{7,1}。
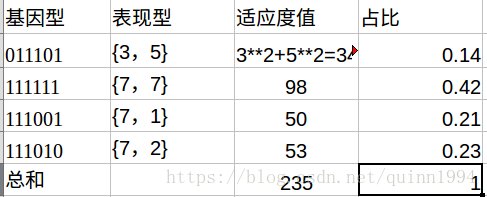
第三步,计算适应度。本例,直接用目标函数作为适应度函数。得到如下表格:
第四步,选择。适应度越高的个体,遗传到下一代的数量越多,这里采用轮盘赌方式。轮盘赌是典型的几何概率模型,其特点在于其选择概率与适应度大小成正比。在第三步中,计算了4个个体的适应度以及他所占总适应度值的比值将其组成一个概率区域,如下:
接下来,我们随机生成4个[0,1]之间的随机数,{0.15,0.35,0.89,0.75}。根据随机数的大小,来选择个体存活的数量。这里,有两个随机数落在了4#区间,分别有1个随机数落在了1#和2#区间。这样,我们就选出了下一代的个体。
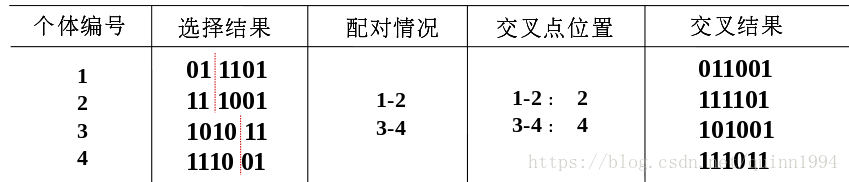
第五步,交配。在这步中会个体间的基因互换,这里采取的是单点互换。首先,选择对群体进行随机配对,然后随机设置交换点的位置,最后互换基因。这里,我们将1-2,3-4,配对并且互换基因,如下:
第六步,变异。在这步中,我们随机选择一个个体,并且随机选择一个位置进行变异。将0变为1,或者将1变为0。
编号 基因型 变异点 变异结果
经过以上过程,我们得到了第二代,对其适应度计算如下:
此时,我们已经发现其解的适应度都得到了提升。实际上本轮已经得到了最佳的解{7,7}。
二. 复杂的多目标函数求解
以上我们的目标函数是不存在冲突的,但是有这样一种冲突的情况,两个目标函数一个要求最大,一个要求最小。某个目标函数的提高需要另一个函数降低作为代价,这样就出现了帕雷托解(pareto)。
我们使用遗传算法解决pareto解有以下几种方法:
1.权重系数转换法
对每个目标函数f(xi)(i=1,2,3,4...)赋予权重wi(i=1,2,3.....),wi为目标函数重要程度。则得到如下线性组合:
这里我们就将多目标转化为单目标函数,将u作为评价函数。
2.并列选择法
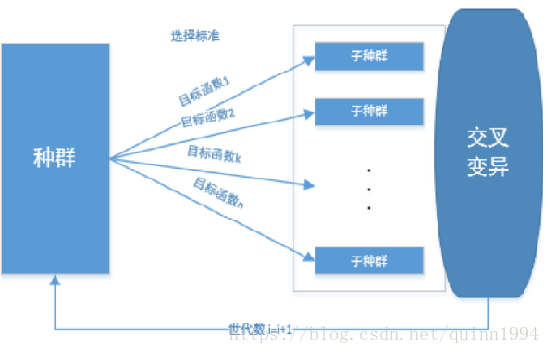
主要步骤:(1)将种群按照目标函数个数等分为子种群,为每个子种群分配一个目标函数。(2)将子种群中的个体按照各自的目标函数选择出适应度高的个体,然后将其组成一个子种群。(3)再将子种群进行交配,变异,生成下一代父亲种群。然后,再重复第一步。
并列选择法的缺点在于易于生成单个目标函数的极端最优解,而较难生成一种多个目标在某种程度上都比较满意的折衷解。
3.排序选择法
排序选择法的基本思想是:基于“pareto最优个体”的概念对群体中的个体进行排序,然后根据这个次序进行种群选择。这样的话就能够让pareto最优个体有更多的机会遗传到下一代。这种方法的缺点是仅仅度量了各个个体之间的优越次序,而并未度量各个个体的分散程度,所以容易生成相似的解,而不是分布较广的多个最优解。
4.共享函数法
针对排序选择方法的缺点,即所求的几个最优解通常是集中于最优解集合的某一个小区域内,而不是分散在整个pareto最优解集合。由此,引出了基于共享函数的小生境技术。该算法对相同个体或类似个体是数目加以限制,以便能够产生出种类较多的不同的最优解。这就引出一个问题,怎么衡量两个个体之间的相似度?这就是小生境数。顾名思义,小生境就是在一个小环境中相似的个体种群。最常见的公式为:
s(d)为共享函数,是表示群体中两个个体之间密切关系程度的一个函数。d(X,Y)为个体X,Y之间的hanmin距离,也是用于衡量个体间相似度的一个函数。在计算出小生境数后,可以是小生境数较小的个体能够有更多的机会被选中,遗传到下一代群体中,即相似程度较小的个体能够有更多的机会被遗传到下一代群体中。
其缺点是:每次选择操作时都需要进行大量的个体之间的优越关系的评价和比价较运算,是算法搜索效率较低。
5.Horn和Nafploitis印的基于小生境pareto多目标遗传算法(NPGA)
类似于上面的并列选择法将每一代个体划分为若干类,每个类别选出若干适应度较大的个体作为一个类的优秀代表组成一个种群,然后交配变异产生新一代种群。基于这种小生境的遗传算法(Niched Genetic Algorithms,NGA),可以更好的保持解的多样性,同时具有很高的全局寻优能力和收敛速度,特别适合于复杂多峰函数的优化问题。
6.Srinvivas和Deb的非支配排序遗传算法NSGA
1980年提出的,在遗传算法的基础上对选择再生方法进行改进:将每个个体按照他们的支配与非支配关系进行再分层,再做选择操作,从而达到目的。这里有几个概念要介绍一下:
pareto支配关系
分层
我理解的分层意思就是取出种群中的非支配个体组成一个小种群(第一个非支配最优层),并赋予其中所有个体一个共享的虚拟适应度值。然后在取出个体后的种群中继续取出非支配个体,再将它们组成一个小种群(第二个非支配最优层),并赋予所有个体一个共享的虚拟适应度值。重复以上步骤,直到原始种群分配完毕,这就叫分层,也叫非支配型排序。伪代码如下:
上面说到,我们要指定共享适应度,算法根据适应度共享对虚拟适应度要重新指定。因而需要引出个体共享后的适应度值,以及共享函数和共享半径。具体的公式这里就不展开了,具体想了解可阅读参考文献3的25页。
因此可以发现,非支配型排序遗传算法有如下问题:
1.计算复杂度较高,O(MN**3)M为目标函数个数,N为种群大小。
2.没有精英策略。精英策略可以一定程度上加速算法执行程度,而且在一定程度上保证已经找到的满意解不会丢失。
3.需要指定共享半径。
针对以上问题有学者(k.Deb 2002)提出了用精英策略快速非支配的遗传算法来解决。
7.带精英策略的非支配排序遗传算法一NSGAII
1).采用快速非支配型排序,降低了算法复杂度。其复杂度降为了O(MN**2)。
2).提出了拥挤度和拥挤度比较算子,代替需要指定共享半径的适应度共享策略。并在快速排序后的同级比较中作为胜出标准。使准pareto解中的个体能扩展到整个pareto域中,并均匀分布,保持了种群的多样性。
3).引入精英策略,扩大采样空间。将父代种群和子代种群合并,保证优良个体能够留存下来。
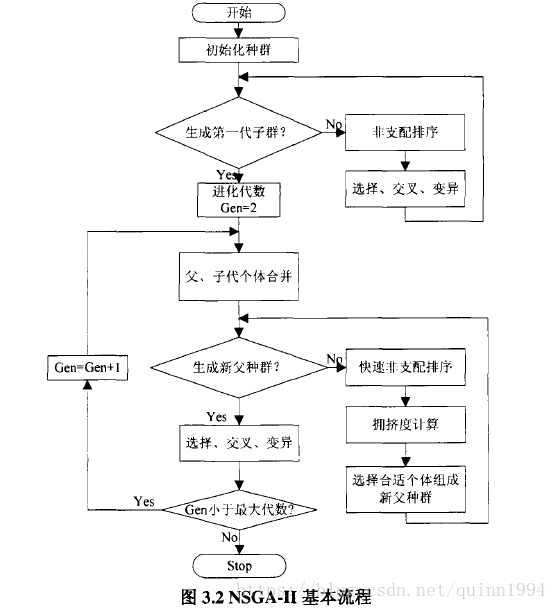
其算法步骤如下:1.首先随机产生数量为n的初始种群,然后对其进行非支配型排序。接下来,就是常规的选择,交叉,变异操作产生第一代子代种群。2.然后,从第二代开始,将父代和子代合并。然后对其进行快速非支配型排序,同时计算每个非支配层的个体进行拥挤度的计算。然后根据非支配关系和拥挤度来选择合适的个体组成新的父代种群。最后通过再通过选择,交叉,变异产生子代。3.接下来,重复第二步。
这里有几个主要的关键技术需要解释一下:
1).快速非支配型排序
2).拥挤度
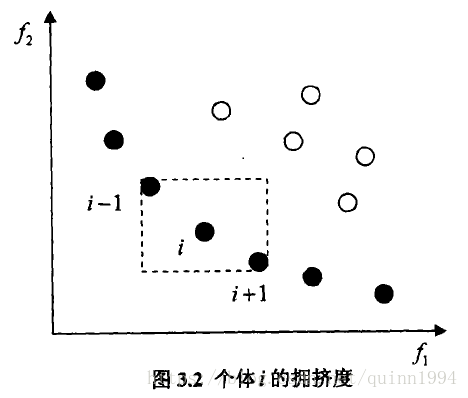
在原来的NSGA中,我们采用共享函数来确保多样性,但需要共享半径。为了解决这个问题,我们提出了拥挤度的概念:在种群种群中的给定点的周围个体密度,用id表示。它指出了在个体i周围包含个体i本身但不包含其他个体的最小的长方形。
拥挤度计算伪代码:
3).拥挤比较算子
经过快速非支配排序和拥挤度计算,种群中的每一个个体都得到了两个属性:非支配序rankn和拥挤度。利用这两个属性,我们可以区分种群中间任意两个个体间的支配和非支配关系。定义拥挤度比较算子,当且仅当irank>jrank或irank=jrank且id>jd,有个体i优于个体j。
4).精英选择策略
将父代优秀的个体与子代合并。
三.NSGAII的实现
算法流程
代码实现:
#Importing required modules
import math
import random
import matplotlib.pyplot as plt
#定义函数1
def function1(x):
value = -x**2
return value
#定义函数2
def function2(x):
value = -(x-2)**2
return value
#Function to find index of list
#查找列表指定元素的索引
def index_of(a,list):
for i in range(0,len(list)):
if list[i] == a:
return i
return -1
#Function to sort by values
# 函数根据指定的值列表排序
'''list1=[1,2,3,4,5,6,7,8,9]
value=[1,5,6,7]
sort_list=[1,5,6,7]
'''
def sort_by_values(list1, values):
sorted_list = []
while(len(sorted_list)!=len(list1)):
# 当结果长度不等于初始长度时,继续循环
if index_of(min(values),values) in list1:
# 标定值中最小值在目标列表中时
sorted_list.append(index_of(min(values),values))
# 将标定值的最小值的索引追加到结果列表后面
values[index_of(min(values),values)] = math.inf
# 将标定值的最小值置为无穷小,即删除原来的最小值,移向下一个
# infinited
return sorted_list
#Function to carry out NSGA-II's fast non dominated sort
#函数执行NSGA-II的快速非支配排序,将所有的个体都分层
'''
郭军p21
1.np=0 sp=infinite
2.对所有个体进行非支配判断,若p支配q,则将q加入到sp中,并将q的层级提升一级。
若q支配p,将p加入sq中,并将p的层级提升一级。
3.对种群当前分层序号k进行初始化,令k=1
4.找出种群中np=0的个体,将其从种群中移除,将其加入到分层集合fk中,该集合就是层级为0个体的集合。
5.判断fk是否为空,若不为空,将fk中所有的个体sp中对应的个体层级减去1,且k=k+1,跳到2;
若为空,则表明得到了所有非支配集合,程序结束
'''
"""基于序列和拥挤距离,这里找到任意两个个体p,q"""
def fast_non_dominated_sort(values1, values2):
S=[[] for i in range(0,len(values1))]
# 种群中所有个体的sp进行初始化 这里的len(value1)=pop_size
front = [[]]
# 分层集合,二维列表中包含第n个层中,有那些个体
n=[0 for i in range(0,len(values1))]
rank = [0 for i in range(0, len(values1))]
# 评级
for p in range(0,len(values1)):
S[p]=[]
n[p]=0
# 寻找第p个个体和其他个体的支配关系
# 将第p个个体的sp和np初始化
for q in range(0, len(values1)):
#step2:p > q 即如果p支配q,则
if (values1[p] > values1[q] and values2[p] > values2[q]) or (values1[p] >= values1[q] and values2[p] > values2[q]) or (values1[p] > values1[q] and values2[p] >= values2[q]):
#支配判定条件:当且仅当,对于任取i属于{1,2},都有fi(p)>fi(q),符合支配.或者当且仅当对于任意i属于{1,2},有fi(p)>=fi(q),且至少存在一个j使得fj(p)>f(q) 符合弱支配
if q not in S[p]:
# 同时如果q不属于sp将其添加到sp中
S[p].append(q)
# 如果q支配p
elif (values1[q] > values1[p] and values2[q] > values2[p]) or (values1[q] >= values1[p] and values2[q] > values2[p]) or (values1[q] > values1[p] and values2[q] >= values2[p]):
# 则将np+1
n[p] = n[p] + 1
if n[p]==0:
# 找出种群中np=0的个体
rank[p] = 0
# 将其从pt中移去
if p not in front[0]:
# 如果p不在第0层中
# 将其追加到第0层中
front[0].append(p)
i = 0
while(front[i] != []):
# 如果分层集合为不为空,
Q=[]
for p in front[i]:
for q in S[p]:
n[q] =n[q] - 1
# 则将fk中所有给对应的个体np-1
if( n[q]==0):
# 如果nq==0
rank[q]=i+1
if q not in Q:
Q.append(q)
i = i+1
# 并且k+1
front.append(Q)
del front[len(front)-1]
return front
# 返回将所有个体分层后的结果
#Function to calculate crowding distance
#计算拥挤距离的函数
'''
高媛p29
1.I[1]=I[l]=inf,I[i]=0 将边界的两个个体拥挤度设为无穷。
2.I=sort(I,m),基于目标函数m对种群排序
3.I[i]=I[i]+(Im[i+1]-Im[i-1])/(fmax-fmin)
'''
def crowding_distance(values1, values2, front):
distance = [0 for i in range(0,len(front))]
# 初始化个体间的拥挤距离
sorted1 = sort_by_values(front, values1[:])
sorted2 = sort_by_values(front, values2[:])
# 基于目标函数1和目标函数2对已经划分好层级的种群排序
distance[0] = 4444444444444444
distance[len(front) - 1] = 4444444444444444
for k in range(1,len(front)-1):
distance[k] = distance[k]+ (values1[sorted1[k+1]] - values2[sorted1[k-1]])/(max(values1)-min(values1))
for k in range(1,len(front)-1):
distance[k] = distance[k]+ (values1[sorted2[k+1]] - values2[sorted2[k-1]])/(max(values2)-min(values2))
return distance
# 返回拥挤距离
#函数进行交叉
def crossover(a,b):
r=random.random()
if r>0.5:
return mutation((a+b)/2)
else:
return mutation((a-b)/2)
#函数进行变异操作
def mutation(solution):
mutation_prob = random.random()
if mutation_prob <1:
solution = min_x+(max_x-min_x)*random.random()
return solution
pop_size = 20
max_gen = 100
# 迭代次数
#Initialization
min_x=-55
max_x=55
solution=[min_x+(max_x-min_x)*random.random() for i in range(0,pop_size)]
# 随机生成变量
gen_no=0
while(gen_no<max_gen):
function1_values = [function1(solution[i])for i in range(0,pop_size)]
function2_values = [function2(solution[i])for i in range(0,pop_size)]
# 生成两个函数值列表,构成一个种群
non_dominated_sorted_solution = fast_non_dominated_sort(function1_values[:],function2_values[:])
# 种群之间进行快速非支配性排序,得到非支配性排序集合
print("The best front for Generation number ",gen_no, " is")
for valuez in non_dominated_sorted_solution[0]:
print(round(solution[valuez],3),end=" ")
print("\n")
crowding_distance_values=[]
# 计算非支配集合中每个个体的拥挤度
for i in range(0,len(non_dominated_sorted_solution)):
crowding_distance_values.append(crowding_distance(function1_values[:],function2_values[:],non_dominated_sorted_solution[i][:]))
solution2 = solution[:]
#生成了子代
while(len(solution2)!=2*pop_size):
a1 = random.randint(0,pop_size-1)
b1 = random.randint(0,pop_size-1)
# 选择
solution2.append(crossover(solution[a1],solution[b1]))
#随机选择,将种群中的个体进行交配,得到子代种群2*pop_size
function1_values2 = [function1(solution2[i])for i in range(0,2*pop_size)]
function2_values2 = [function2(solution2[i])for i in range(0,2*pop_size)]
non_dominated_sorted_solution2 = fast_non_dominated_sort(function1_values2[:],function2_values2[:])
# 将两个目标函数得到的两个种群值value,再进行排序 得到2*pop_size解
crowding_distance_values2=[]
for i in range(0,len(non_dominated_sorted_solution2)):
crowding_distance_values2.append(crowding_distance(function1_values2[:],function2_values2[:],non_dominated_sorted_solution2[i][:]))
# 计算子代的个体间的距离值
new_solution= []
for i in range(0,len(non_dominated_sorted_solution2)):
non_dominated_sorted_solution2_1 = [index_of(non_dominated_sorted_solution2[i][j],non_dominated_sorted_solution2[i] ) for j in range(0,len(non_dominated_sorted_solution2[i]))]
#排序
front22 = sort_by_values(non_dominated_sorted_solution2_1[:], crowding_distance_values2[i][:])
front = [non_dominated_sorted_solution2[i][front22[j]] for j in range(0,len(non_dominated_sorted_solution2[i]))]
front.reverse()
for value in front:
new_solution.append(value)
if(len(new_solution)==pop_size):
break
if (len(new_solution) == pop_size):
break
solution = [solution2[i] for i in new_solution]
gen_no = gen_no + 1
#Lets plot the final front now
function1 = [i * -1 for i in function1_values]
function2 = [j * -1 for j in function2_values]
plt.xlabel('Function 1', fontsize=15)
plt.ylabel('Function 2', fontsize=15)
plt.scatter(function1, function2)
plt.show()四.总结
相对于单目标函数求解,多目标函数求解明显难度提升了好几个数量级,其核心问题在于出现了pareto解。我们需要权衡各个目标函数之间的利弊,选择合适算法来求解。本篇通过引出一个简单的多目标函数例子,介绍了7种算法着重介绍了其中的NSGAII算法,其核心策略在于对快速非支配算法的设计,拥挤度的计算,拥挤度算子的设计,精英策略的设计。由于篇幅较长,里面几个的概念不容易理解,程序中也有一些技巧不易察觉。但是静下心来慢慢琢磨,还是挺有收获的。本人才疏学浅,如有纰漏,望诸位读者不吝赐教。祝好!
五.参考文献:
- 九二. 遗传算法学习--多目标优化中的遗传算法[DB/OL]. https://www.cnblogs.com/lomper/p/3831428.html
- variousme. 小生境遗传算法[EB/OL]. http://blog.sina.com.cn/s/blog_714e46f80100o1pp.html.
- 卢小亭. 多目标优化遗传算法选择方法的研究与改进[D]. 合肥:安徽理工大学, 2008. 20-25
- 高媛. 非支配排序遗传算法NSGA的研究与应用_[D]. 杭州:浙江大学, 2006. 20-24
- devilmaycry812839668. 带精英策略的快速非支配排序遗传算法 NSGA-II 算法[EB/OL]. https://www.cnblogs.com/devilmaycry812839668/p/6268408.html.
- 郭军. 带精英策略的非支配排序遗传算法优化研究[D]. 沈阳:辽宁大学, 2017. 21-25
- A, Konak, DW, Coit. Multi-objective optimization using genetic algorithms: A tutorial[J]. Reliability Engineering and System Safety, 2006, 91(9): 992-1007
- Duyuankai1992. 使用python做遗传算法与基于遗传算法的多目标算法[EB/OL]. https://blog.csdn.net/qq_37879432/article/details/80457054.
- Alex.遗传算法-python实现[EB/OL]. http://www.cnblogs.com/biaoyu/p/4865368.html