将各类型优化方法总结下方便查阅,大体分为:一阶梯度依赖的,二阶梯度依赖的;不依赖梯度的优化方法。
1)一阶梯度依赖的优化方法
1.1)GD:Gradient Descent
这个很好理解,根据梯度
来指导下一步优化方向。
梯度来源于
沿着某方向
的方向导数:
.
其中变化(增长)最快的方向及导数值称为梯度:
1.2)Moment GD
[带有动量的GD](On the momentum term in gradient descent learning algorithms),其基本思路是,设想如果当前的梯度方向与历史累积的方向相同,是不是可以加大这个方向上的步幅,以加快收敛速度;若震荡的梯度,则是不是可以互相抵消,避免多走弯路,以加快收敛速度。[同向累计,反向抵消]如下,
另外一种更新方式如下(需要见证下,来自安德鲁的课程):
[ bias correct ]
假设一个时间变量 ,如果
得到 的期望值是 的期望的指数衰减值。
1.3) NAG
NAG:Nesterov accelerated gradient [A method for unconstrained convex minimization problem with the rate of convergence o(1/k2)]
基本想法是,提前预知下一步的位置是上坡,则减小步幅,提前预支下一步的位置是下坡,则增大步幅。
1.4) RMSprop
RMSprop GD :root mean square
是Hitton提出的,基本思路是Bias-correct,不过是利用
与
的正相关关系,找到梯度的期望来指导当前的参数更新。
假设
则
1.5) Adam
Adam GD:adaptive moment estimation [2015-Adam, A Method for Stochastic Optimization]
结合了moment和RMSP的两者优点,如下:
并且在online-learning时,Adam也是收敛的。
1.6) AdaGrad
AdaGrad Descent [ Adaptive Subgradient Methods for Online Learning
and Stochastic Optimization]
基本思路: 自适应学习率,能够对频繁更新的参数采取更小的步幅;对更新不频繁的参数采取更大的步幅。非常适合稀疏数据的学习。其中
表示到update当时为止,所有已计算的梯度的平方和。
1.7) AdaDelt
AdaDelt GD [ An Adaptive Learning Rate Method]
AdaGrad存在问题:平方和的累和会一直增加下去,导致分母部分无限大,梯度被削弱至非常小,参数不再更新。而AdaDelt则刚好为解决这问题而诞生,借助指数衰减平均
的思路来避免所有历史梯度^2的平均加和。
首先参数的增量值
用梯度的期望来表示为:
然后增量值的期望值也用指数衰减平均表示
用梯度的期望,增量值的期望估计(当次的不知道,用前一次的来估计),以及当前梯度来指导学习的方向。
作者在原文里解释,是用一阶导数去估计二阶导数Hassion矩阵。
补充阅读
AdaMax
Nadam:Nesterov Momentum into Adam
DFP
DFBS
AdamW
估计函数的二阶导数,其实好多方法都是对二阶导数的估计得来的,比如DFP/DFBS/AdaDelt。
2)二阶梯度依赖的优化方法
各种适应性,在有道云笔记上有部分内容。
牛顿下降法
求解
,等价于找到
对应的
值。
要想找到函数的零值点,可以根据其泰勒展开
作近似逼近,另f=0,得到
,由于导数是描述增幅的,那么对应的
就相应的比
要更靠近零值点,如下图。
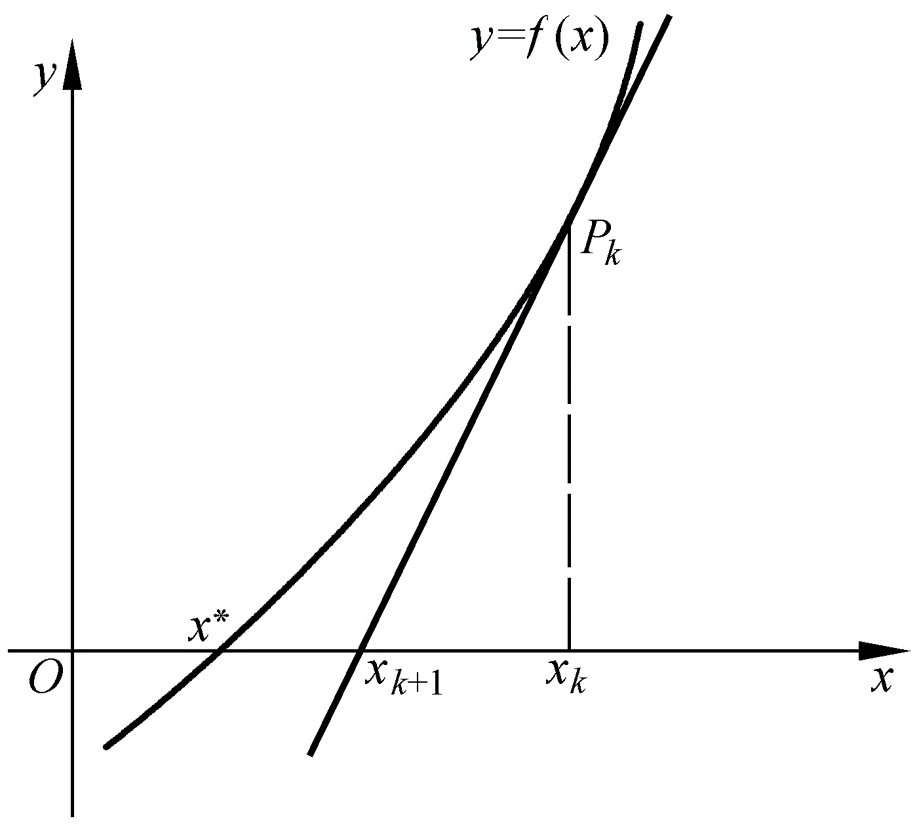
那么回到等价问题上,找到函数 的零值点,我们对 在某处 做一阶展开 ,于是得到迭代关系 可以不断逼近 的零值点。
3)不依赖梯度的优化方法
3.1)Gradient Boost
Gradient Boost的梯度方向是由最终label与当前的预测label之间的差距给出的,详细见GB
3.2)Constractive Divergence
对比散度类方法,主要是根据条件随机场的收敛性,可以根据下次采样比当前状态更靠近稳定最优解,来给出优化方向,详细见RBM。
梯度相关的trick
1) ReLU等激活函数的各种类型。
2) Gradient Clip,常用在RNN类方法中。
3) Batch Normalize,对所有网络都使用。(Group Normalization, Switchable Normalization等改进的方法)
4) 正则化方法及各种变形改进。(DIN里面有个根据数据对梯度作约束的正则,非常有意思)
未完待续
后续会补充能查到的资料,并且会讲解如何在TF里面实现自定义的Gradient Optimize Operation。