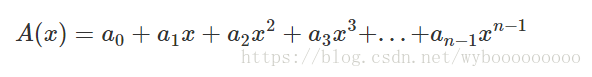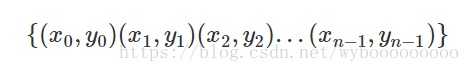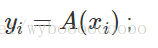实在是美丽的数学啊

关于傅里叶变换的博客讲的很细致图片非常易于理解http://blog.jobbole.com/70549/

大概能明白傅里叶变换是干吗的了

但是还是不能明白为什么用傅里叶变换来算多项式求和

在多项式中，DFT就是系数表式转换成点值表示的过程。

我们熟知的是多项式的系数表示法，通过给定一组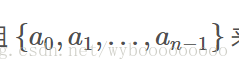来确定一个唯一的多项式：

而多项式还可以有另一种表示法，称为点值表示法：

其中

可以证明，对一组互不相同的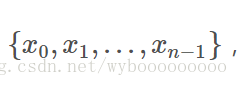该方法也可以唯一地表示一个多项式。

为什么要引入点值表示法这个并不“直观”的形式呢？下表显示了它的好处：

执行运算	系数表示	点值表示
A(x)+B(x)	O(n)	O(n)
A(x)∗B(x)	O(n2)	O(n)

*当然，点值表示法下的运算均要求 A(x)和 B(x) 所取的点集 {x0,x1,...,xn−1}是相同的，且运算出的 C(x) 也为点值表示法。

FFT只是快速的求DFT的方法罢了，不是一个新的概念。在ACM-ICPC竞赛中, FFT算法常被用来为多项式乘法加速。

FFT原理就是通过奇偶分开，把规模减半，递归分治在O(nlogn）时间内完成DFT运算

普通的计算多项式乘法的计算，时间复杂度O(n2)O(n2)。而FFT先将多项式点值表示（O(nlogn)），在O(n)下完成对点值的乘法，再以O(nlogn)O(nlog⁡n)完成IFFT，重新得到系数表示。

利用FFT求卷积

普通的计算多项式乘法的计算，时间复杂度O(n2)O(n2)。而FFT先将多项式点值表示（O(nlogn)），在O(n)下完成对点值的乘法，再以O(nlogn)完成IFFT，重新得到系数表示。

步骤一（补0）

在两个多项式前面补0，得到两个2n次多项式，设系数向量分别为v1v1和v2v2。

步骤二（求值）

使用FFT计算f1=DFT(v1)和f2=DFT(v2)。则f1f1与f2f2为两个多项式在2n2n次单位根处的取值（即点值表示）。

步骤三（乘法）

把f1f1与f2f2每一维对应相乘，得到ff，代表对应输入多项式乘积的点值表示。

步骤四（插值）

使用IFFT计算v=IDFT(f)，其中vv就是乘积的系数向量。

综上

fft(x1, len, 1);
fft(x2, len, 1);
for (int i = 0;i < len;i++) {
    x[i] = x1[i] * x2[i];
}
fft(x, len, -1);

FFT算法步骤：https://wenku.baidu.com/view/8bfb0bd476a20029bd642d85.html

kuangbin模板：

const double PI = acos(-1.0);
//复数结构体
struct complex
{
    double r,i;
    complex(double _r = 0.0,double _i = 0.0)
    {
        r = _r; i = _i;
    }
    complex operator +(const complex &b)
    {
        return complex(r+b.r,i+b.i);
    }
    complex operator -(const complex &b)
    {
        return complex(r-b.r,i-b.i);
    }
    complex operator *(const complex &b)
    {
        return complex(r*b.r-i*b.i,r*b.i+i*b.r);
    }
};
/*
 * 进行FFT和IFFT前的反转变换。
 * 位置i和 （i二进制反转后位置）互换
 * len必须去2的幂
 */
void change(complex y[],int len)
{
    int i,j,k;
    for(i = 1, j = len/2;i < len-1; i++)
    {
        if(i < j)swap(y[i],y[j]);
        //交换互为小标反转的元素，i<j保证交换一次
        //i做正常的+1，j左反转类型的+1,始终保持i和j是反转的
        k = len/2;
        while( j >= k)
        {
            j -= k;
            k /= 2;
        }
        if(j < k) j += k;
    }
}
/*
 * 做FFT
 * len必须为2^k形式，
 * on==1时是DFT，on==-1时是IDFT
 */
void fft(complex y[],int len,int on)
{
    change(y,len);
    for(int h = 2; h <= len; h <<= 1)
    {
        complex wn(cos(-on*2*PI/h),sin(-on*2*PI/h));
        for(int j = 0;j < len;j+=h)
        {
            complex w(1,0);
            for(int k = j;k < j+h/2;k++)
            {
                complex u = y[k];
                complex t = w*y[k+h/2];
                y[k] = u+t;
                y[k+h/2] = u-t;
                w = w*wn;
            }
        }
    }
    if(on == -1)
        for(int i = 0;i < len;i++)
            y[i].r /= len;
}

沃尔什变换https://www.cnblogs.com/ACMLCZH/p/8022502.html

主要功能是求：，其中为集合运算符。