矩形函数:
Π(t)={1,|t|<120,|t|≥12
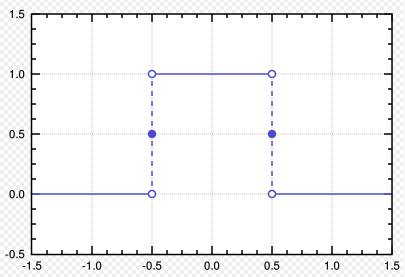
对其进行傅里叶变换,我们有(需要运用欧拉公式的变形公式,详见傅里叶级数推导过程(2)、(3)式):
FΠ(s)=∫∞−∞e−2πistΠ(t)dt=∫12−12e−2πistdt=−12πise−2πist∣∣∣t=12t=−12=1πs(eπis−e−πis)2i=sin(πs)πs
我们定义
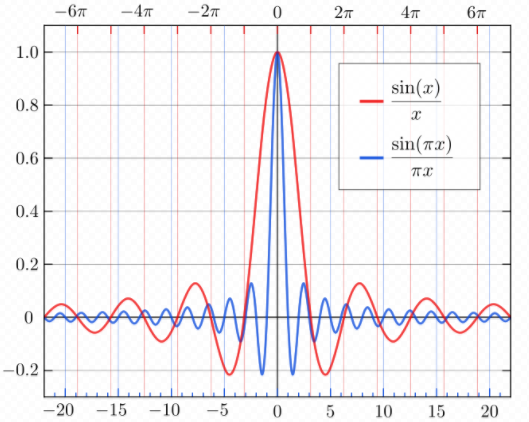
sinc(x)=sin(πx)πx
,我们称其为归一化
sinc
函数,在数字信号处理中常用;
而对于
sinc(x)=sin(x)x
,我们称其为未归一化的
sinc
函数,在数学中常用。
二者的图像如下:
扫描二维码关注公众号,回复:
2837092 查看本文章

三角函数
Λ(t)={1−|t|0,|t|≤1,|t|>1
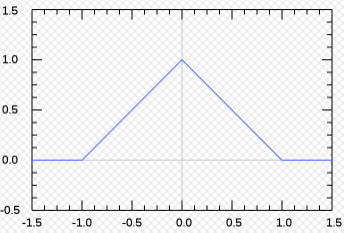
对其进行傅里叶变换,我们有(需要运用分部积分法,详见微积分相关内容):
FΛ(s)=∫∞−∞e−2πistΛ(t)dt=∫0−1e−2πist(1+t)dt+∫10e−2πist(1−t)dt=∫0−1(1+t)d(e−2πist−2πis)+∫10(1−t)d(e−2πist−2πis)=(1+t)(e−2πist−2πis)∣∣∣0−1−∫0−1(e−2πist−2πis)d(1+t)+(1−t)(e−2πist−2πis)∣∣∣10−∫10(e−2πist−2πis)d(1−t)=(1+t)(e−2πist−2πis)∣∣∣0−1−∫10(e−2πis(k−1)−2πis)dk+(1−t)(e−2πist−2πis)∣∣∣10−∫01(e−2πis(1−k)−2πis)dk=(1+t)(e−2πist−2πis)∣∣∣0−1−(e2πis−2πise−2πisk−2πis)∣∣∣10+(1−t)(e−2πist−2πis)∣∣∣10−(e−2πis−2πise2πisk2πis)∣∣∣01=2−e2πis−e−2πis4π2s2
利用欧拉公式,我们有:
FΛ(s)=2−(cos2πs+isin2πs)−(cos2πs−isin2πs)4π2s2=2−2cos2πs4π2s2=2−2(1−2sin2πs)4π2s2=sin2πsπ2s2=sinc2(s)
最后我们来看高斯函数的傅里叶变换
高斯分布(又称正太分布)公式如下:
f(x)=12π−−√σe−(x−μ)22σ2
即
X
~
N(μ,σ2)
我们令
μ=0
,
σ2=12π
,用
t
代替
x
成为自变量,则有以下高斯函数特例:
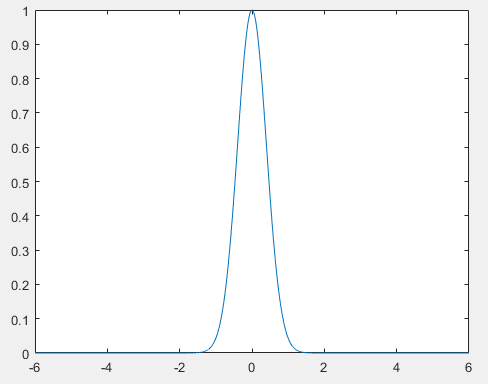
f(t)=e−πt2(1)
对
(1)
式进行傅里叶变换,为了方便,我们将
Ff
写作
F
,则有
F(s)=Ff(s)=∫+∞−∞e−2πistf(t)dt(2)
两边同时对
s
求导,
F′(s)=∫+∞−∞dds(e−2πist)e−πt2dt=∫+∞−∞(−2πit)e−2πiste−πt2dt=i∫+∞−∞e−2πistd(e−πt2)=ie−2πiste−πt2∣∣t=+∞t=−∞−i∫∞−∞e−πt2d(e−2πist)(3)
对于
(2)
式,我们将等式右边拆分成两个部分进行计算
对于第一部分,我们不难发现,
ie−2πist=icos(2πst)+sin(πst)
,由于
sinx
、
cosx
是有限的,即取值范围都在
[−1,1]
,因此,
ie−2πist
的取值也是有限的,即在复平面内模长为1的圆上取值;而当
t→∞
时
e−πt2→0
。一个有限的数与零相乘,其结果为0,故
ie−2πiste−πt2∣∣t=+∞t=−∞=0(4)
第二部分:
i∫+∞−∞e−πt2d(e−2πist)=i∫+∞−∞−2πise−2πiste−πt2dt=2πs∫+∞−∞e−2πiste−πt2dt=2πsF(s)(5)
由
(3)
、
(4)
、
(5)
式,我们可以得到:
F′(s)=0−2πsF(s)=−2πsF(s)
运用分离变量法解该常微分方程,我们可以得到:
F(s)=F(0)e−πs2(6)
根据
(2)
式,我们可以得到:
F(0)=∫+∞−∞e−2πi0tf(t)dt=∫+∞−∞e−πt2dt(7)
下面我们先来计算定积分
∫∞−∞e−πt2dt
令
g(x)=∫∞−∞e−πx2dx
,则
g2(x)=(∫+∞−∞e−πx2dx)2=∫+∞−∞e−πx2dx∫+∞−∞e−πy2dy=∫+∞−∞∫+∞−∞e−πx2e−πy2dxdy=∫+∞−∞∫+∞−∞e−π(x2+y2)dxdy
我们对
x
、
y
进行极坐标变换,可得:
g2(x)=∫2π0∫+∞0e−πρ2ρdρdθ=∫+∞02πe−πρ2ρdρ=π∫+∞0e−πρ2d(ρ2)=π(1−πe−πρ2∣∣∣+∞0)=−(0−1)=1(8)
由
(6)
、
(7)
、
(8)
式,我们有
F(s)=Ff(s)=e−πs2(9)
这个结果表示,高斯函数
f(t)=e−πt2
经傅里叶变换后的图像形状,与原图像形状是一样的




