目录
1.4.4 递归消除
1.4.4.1 空间成本
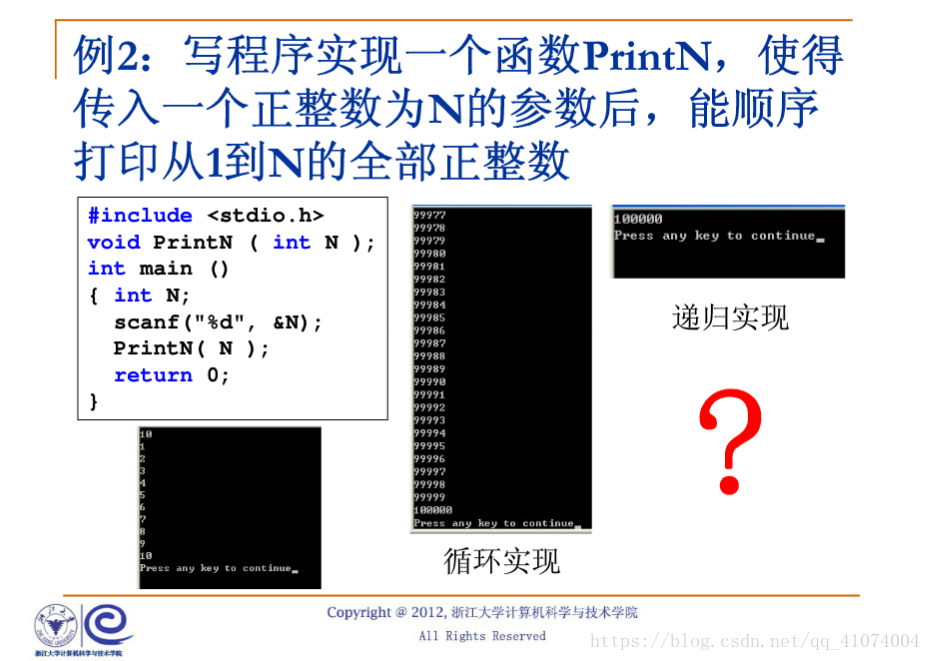
递归算法所消耗的空间量主要取决于递归深度,所以与同一算法的迭代相比,递归会使用更多的空间量,进而影响实际的运行速度。在浙大的数据结构视频开始,举了一个打印1到n的例子,一个递归,一个迭代。当数字太大时,递归算法根本不执行。
对于操作系统来说,为了实现递归调用需要花费大量额外的时间去创建、维护和销毁各递归实例,这些会使得计算的负担雪上加霜。所以在对运行速度要求极高、存储空间需要精打细算时,往往会将递归算法改写为等价的非递归版本。首先在使用一门语言时,要学着去写递归,尝试着去使用递归的方式去解决问题,然后在能很好的掌握之后,再反过来将递归改写为等价的非递归形式提高空间利用率和运行时间。
1.4.4.2 尾递归及其消除
尾递归(tail recursion) :在线性递归算法中,递归调用在递归实例中恰好以最后一步操作的形式出现
0001 void reverse ( int* A, int lo, int hi ) { //数组倒置(多递归基递归版)
0002 if ( lo < hi ) {
0003 swap ( A[lo], A[hi] ); //交换A[lo]和A[hi]
0004 reverse ( A, lo + 1, hi - 1 ); //递归倒置A(lo, hi)
0005 } //else隐含了两种递归基(0 or 1)
0006 } //O(hi - lo + 1)
上面的算法代码中最后一步操作,是对除了首、末元素之后总长缩减两个单元的子数组进行递归倒置,即属于典型的尾递归。属于尾递归形式的算法,均可以简捷地转换为等效的迭代版本,例如将上面的递归改写如下 :
0001 void reverse ( int* A, int lo, int hi ) { //数组倒置(直接改造而得的迭代版)
0002 next: //算法起始位置添加跳转标志
0003 if ( lo < hi ) {
0004 swap ( A[lo], A[hi] ); //交换A[lo]和A[hi]
0005 lo++; hi--; //收缩待倒置区间
0006 goto next; //跳转至算法体的起始位置,迭代地倒置A(lo, hi)
0007 } //else隐含了迭代的终止
0008 } //O(hi - lo + 1)
新的迭代版本与递归等效,但是使用了goto语句有悖于结构化程序设计的原则,平时应该避免使用,可将上面的迭代改为下面的while形式。
0001 void reverse ( int* A, int lo, int hi ) { //数组倒置(规范整理之后的迭代版)
0002 while ( lo < hi ) //用while替换跳转标志和if,完全等效
0003 swap ( A[lo++], A[hi--] ); //交换A[lo]和A[hi],收缩待倒置区间
0004 } //O(hi - lo + 1)
尾递归的判断方法应该依据对算法实际执行过程的分析,而不是算法的外在形式,只有当算法(除平凡递归基外)任一实例都终止与这一递归调用时,才属于尾递归。
1.4.5 二分递归
分而治之(divide-and-conquer):将一个问题分若干规模更小的子问题,再通过递归机制分别求解.这种分解持续进行,直到子问题缩减为平凡情况。
1.4.5.1 数组求和
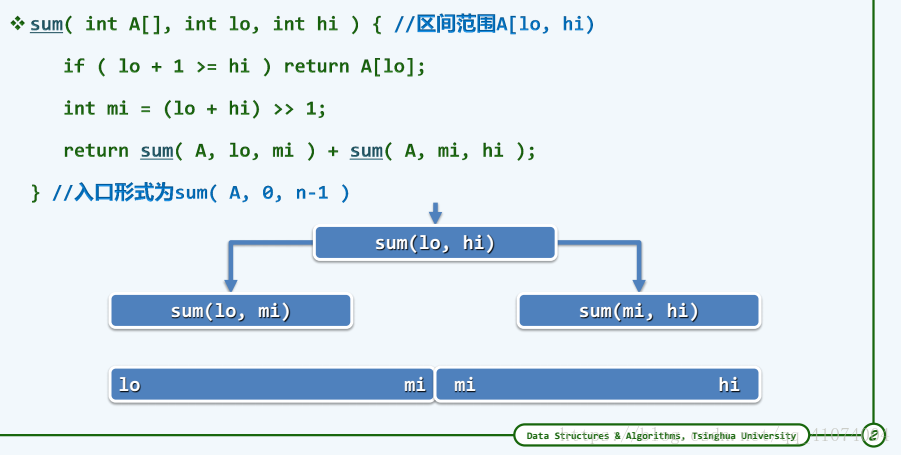
0001 int sum ( int A[], int lo, int hi ) { //数组求和算法(二分递归版,入口为sum(A, 0, n))
0002 if ( lo == hi ) { //如遇递归基(区间长度已降至1),则
0003 return A[lo]; //直接返回该元素
0004 else{ //否则(一般情况lo < hi),则
0005 int mi = ( lo + hi ) >> 1; //以居中单元为界,将原区间均分
0006 return sum ( A, lo, mi ) + sum ( A, mi, hi ); //递归对各子数组求和,然后合计
0007 }
0008 } //O(hi - lo),线性正比于区间的长度
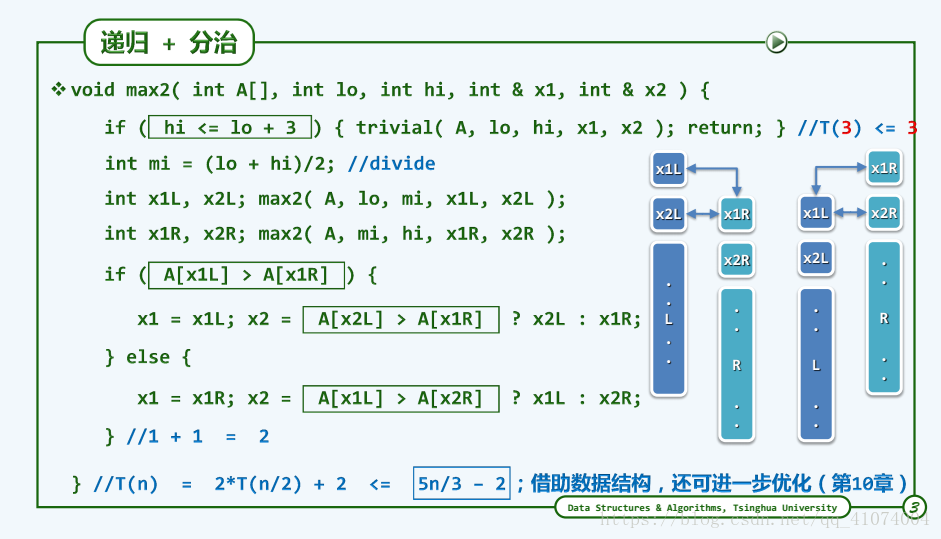
1.4.5.2 Max2
附上一个翻译的主定理(master theorem)
1.5 动态规划
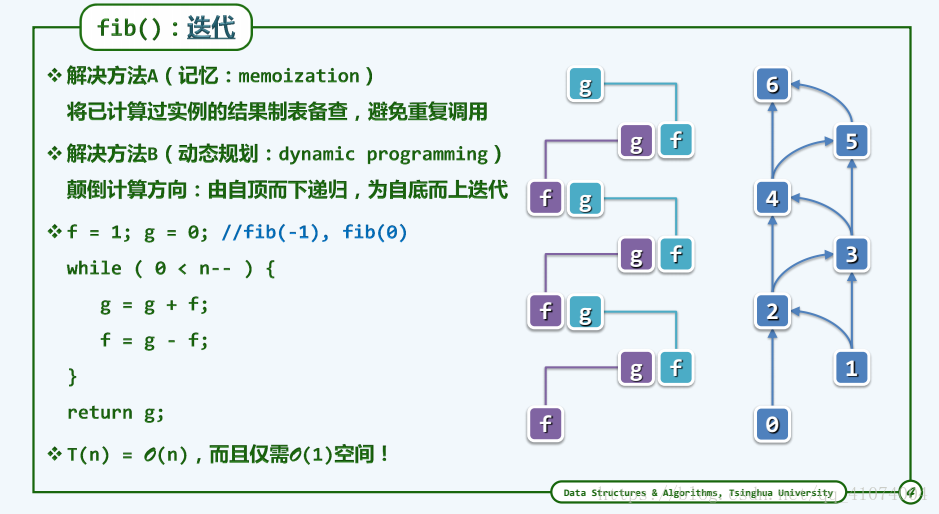
1. 动态规划的目的:
make it work(递归可以保证)
make it right(递归可以保证)
make it fast(迭代可以保证)
2. 递归对于资源的消耗大而且O(n)比较大,然而迭代可以降低对存储空间的使用,有时亦可以降低O(n)
3. 子序列:由原序列中若干个元素,按原来相对次序排列而成的新的序列。
4. 最长公共子序列(longest common subsequence, LCS)是两个序列中,在其相同的子序列中长度最长的那个子序列,可能含有多个。
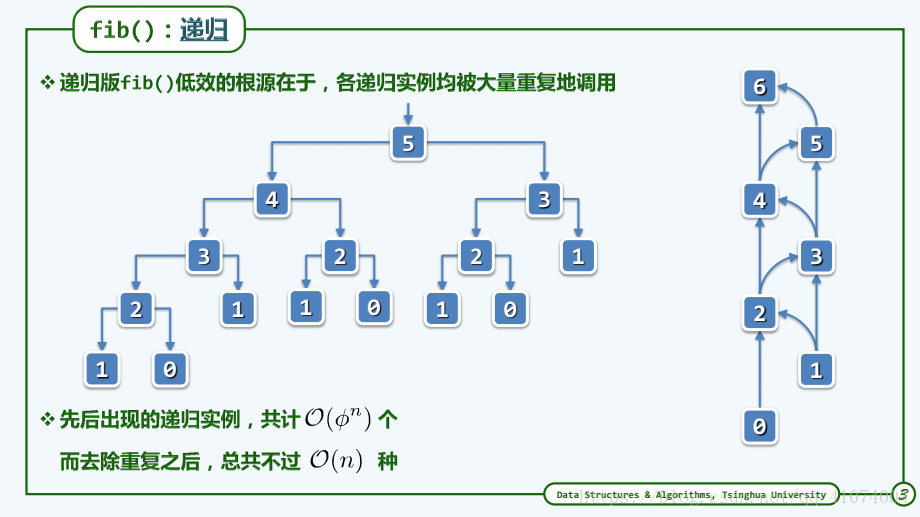
1.5.1 Fibonacci数 : 二分递归
0001 __int64 fib ( int n ) { //计算Fibonacci数列的第n项(二分递归版):O(2^n)
0002 return ( 2 > n ) ?
0003 ( __int64 ) n //若到达递归基,直接取值
0004 : fib ( n - 1 ) + fib ( n - 2 ); //否则,递归计算前两项,其和即为正解
0005 }
递推方程
Fib() 递归方程的封底估算
FLOPS(即“每秒浮点运算次数”,“每秒峰值速度”),是“每秒所执行的浮点运算次数”(floating-point operations per second)的缩写。它常被用来估算电脑的执行效能,尤其是在使用到大量浮点运算的科学计算领域中。正因为FLOPS字尾的那个S,代表秒,而不是复数,所以不能省略掉。
在这里所谓的“浮点运算”,实际上包括了所有涉及小数的运算。这类运算在某类应用软件中常常出现,而它们也比整数运算更花时间。现今大部分的处理器中,都有一个专门用来处理浮点运算的“浮点运算器”(FPU)。也因此FLOPS所量测的,实际上就是FPU的执行速度。而最常用来测量FLOPS的基准程式(benchmark)之一,就是Linpack。
1GHz 就是每秒十亿次(=10^9)运算,如果每次运算能完成两个浮点操作,就叫 2G FLOPS(每秒二十亿次浮点操作)。现在家用的双核计算机通常都能达到每秒四十亿次运算(2*2.0GHz)左右的水平,浮点性能大约是上百亿次(=10^10)浮点操作。
Fib()递归跟踪
Ο(1)表示基本语句的执行次数是一个常数,一般来说,只要算法中不存在循环语句,其时间复杂度就是Ο(1)。其中Ο(log2n)、Ο(n)、 Ο(nlog2n)、Ο(n2)和Ο(n3)称为多项式时间,而Ο(2n)和Ο(n!)称为指数时间。计算机科学家普遍认为前者(即多项式时间复杂度的算法)是有效算法,把这类问题称为P(Polynomial,多项式)类问题,而把后者(即指数时间复杂度的算法)称为NP(Non-Deterministic Polynomial, 非确定多项式)问题。
1.5.2 Fibonacci数 : 迭代