树状数组概念:
树状数组是一种非常优秀&神奇的数据结构。可以做到区间查询、单点修改,两种操作的复杂度都为log(n),其空间复杂度为O(n)。
理解树状数组的关键在于理解二进制,曾有一个大神对我说:“这个世界本来就是二进制的,人非要主观的构建一个十进制” ,我并没有能力证明这句话的正确性,但我认为这句话放在树状数组这里是非常助于理解的(因为这种数据结构就是基于二进制的)。
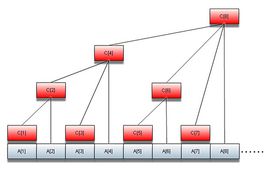
先从百度借张图,没错的,红色部分就是传说中的树状数组了。
观察片刻,不难发现:
C1 = A1
C2 = A1+A2
C3 = A3
C4 = A1+A2+A3+A4
C5 = A5
C6 = A5+A6
C7 = A7
C8 = A1+A2+A3+A4+A5+A6+A7+A8然而为什么会有这样的规律呢?当然是因为树状数组奇妙的原理了。
原理:
提到树状数组原理,通常我们首先想到的就是lowbit函数,这个函数贯穿树状数组的所有功能和实现,同样也是理解树状数组的关键。
lowbit():
随便打开一个树状数组的代码,我们一定可以一眼找到一个宏定义或者函数,形如:
#define lowbit(x) (x&-x) //宏定义写法 int lowbit(int x) { return x&-x; } //函数写法
两种写法显然本质上是相同的,但是很多OIers其实并不理解为什么要这么写,而只是背过了代码。对于lowbit的理解就涉及到树状数组最根本的原理了。我们看下图,举个栗子。
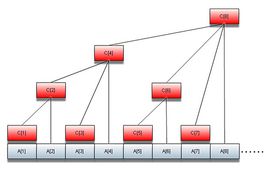
栗子:我们以下图c[7]为例,我们该如何判断c[6]所代表区间的范围呢?
首先写出c[7]的二进制:0111,然后取二进制下该数从右向左的第一个1及后面的0取出,得到1,也就是十进制下的1,即c[7]所包含的区间范围长度。其实转为二进制后的7每一个1都代表树状数组上的一个节点。具体模拟一下,我们想要将最后一个1及后面的0取出,0111可以看作0110+0001,将0110转为十进制后等于6,则c[7]的范围就是 [6 + 1, 7] ,同理继续求c[6]的范围,0110 = 0100 + 0010 将0100转为十进制后等于4,则c[6]的范围就是 [4 + 1, 6]。最后求一下c[4]的取值范围(有点特殊) 0100 = 0100 + 0000 将0000转为十进制后等于0,则c[4]的范围就是 [0 + 1, 4]。
看到这,问题的关键就只剩然后把某个数从右向左的第一个1及后面的0取出了,也就是lowbit函数所做的事情。
lowbit()这行代码到底在做什么?我们需要先明白一些小知识。
1、反码 = 原码每一位取反。
2、补码 = 反码 + 1。
3、计算机中,负数使用补码来表示的。
那么再来看一下上面的代码:
return x & -x;
我们以76为例,我们来做一下以上操作 76 & -76
忽略符号位后效果如下:
76转二进制:0100 1100
-76的二进制:1011 0100
0100 1100
& 1011 0100
= 0000 0100
神奇的大功告成了。
这样有道理吗?肯定是有的,由于反码 = 原码取反 补码 = 反码 + 1,则补码与原码除了最后加的1,其余部分一定相反,与运算后都是0。而最后加1并进位后,一定会使末尾一段再次反过来,直到遇到0,无法进位为止,而第一个遇到的0,一定就是原码中从右向左第一个1。
最后我们也得出 c[l] 所包含的数为a[i - lowbit(i) + 1] ~ a[i] 共lowbit(i)个数字。
区间查询:
首先树状数组本身维护的就是区间和,但是查询时有一个问题就是:查询区间并不一定是树状数组所维护的整区间。
借上图,比如我们要求区间 [4,7] 的区间和。
于是我们先运用前缀和的思想,将问题简化为求[1,7]的区间和 - [1,4]的区间和。
然后我们来思考[1,n]区间和的求法:我们已知树状数组上的节点c[i]代表原数组上a[i - lowbit(i) + 1]到a[i]的和,那么我们考虑求1~n的区间和,则最后的ans中一定不包含a[n + 1],而不包含a[n + 1]的位置我们首选c[n](c[n] 包含的区间一定在c[n + 1] 之前),现在ans += c[n] 我们就已经统计了部分答案,我们也知道我们刚刚统计上的答案一定是原数组上 a[i - lowbit(n) + 1] 到 a[n] 的和,共计lowbit(n)个数被统计到了,于是问题转化为求[1,n - lowbit(n)]的区间和。以此类推,我们可以通过lowbit将[1,n]的区间和求出。
总结一下:sum[i][j] = sum[1][j] - sum[1][i];
for (int i = n; i != 0; i -= lowbit(i)) ans += c[i];
sum[1][n] = ans;
代码如下:
int Query(int x) { int sum = 0; for(int i = x; i; i -= lowbit(i)) //注意循环终止条件 sum += tree[i]; return sum; }
单点修改:
由于树状数组维护的是前缀和,单点修改时我们还要考虑修改包含该节点的点,将这些点全部修改完成后,单点修改完成。
举个栗子:我们对第P个元素进行修改。我们需要找到许多包含P的c[i],将他们一一修改。那么那些c[i]需要修改呢?
首先需要修改的c[i]编号必然大于P,范围必然包括P,且lowbit(i) 一定大于 lowbit(P)。
于是我们得出 i >= P > i - lowbit(i)
我们设P的二进制为 0101 1010
我们先从小到大推测一下i可能是多少。
设i为abcd efgh,由于lowbit(i) 一定大于 lowbit(P),得出i为abcd ef00,后二位确定。其他六位若本来不是1则也可能为1(原因是原来为1的话按此方法推i会小于P),如果这时f = 0,又因为P > i - lowbit(i) 我们得知i为0101 1100(为了满足P > i - lowbit(i))。
我们继续推出abcde为1的情况,同样为最后一个1后面的都是0,1前面的与P相同。
我们列出所有可能:
0101 1100
0110 0000
1000 0000
我们发现这些符合要求的i是通过不断加本身的lowbit找出的。
没错就是这样!!!(逃!)大家可以枚举试一试。
代码如下:
void Add(int x, int k) { for (int i = x; i <= n; i += lowbit(i)) //注意循环终止条件 tree[i] += k; }
代码实现:
顺便说一下树状数组的初始化:直接用单点修改做就行了。没什么问题。
#include<iostream> #include<cstdio> #define lowbit(x) (x&-x) const int MAXN=500010; int n,m; int x,y,z; int tree[MAXN]; void Add(int x,int k) { for(int i=x;i<=n;i+=lowbit(i)) tree[i]+=k; } int Query(int x) { int sum=0; for(int i=x;i;i-=lowbit(i)) sum+=tree[i]; return sum; } int main() { scanf("%d%d",&n,&m); for(int i=1;i<=n;++i) { scanf("%d",&x); Add(i,x); } for(int i=1;i<=m;++i) { scanf("%d%d%d",&x,&y,&z); if(x==1) Add(y,z); else std::cout<<Query(z)-Query(y-1)<<std::endl; } return 0; }
总结:
树状数组确实是一种优美到令人惊叹的数据结构。不过它也不是万能的,有不少优点但也有缺点。
优点:代码简单、好写、好调。修改查询时间复杂度都是O(logN),常数还比线段树小。
缺点:必须满足区间减法,一定转化成两个前缀相减。这就使得很多题无法用树状数组解决。