原文转载于:https://blog.csdn.net/chybin500/article/details/78470705
这一篇博文是【 AI学习路线图】系列文章的其中一篇,点击查看目录:AI学习完整路线图
1.组合数
从mm 个不同元素中取出 n(n≤m)n(n≤m)个元素的所有组合的个数,叫做从 mm 个不同元素中取出 nn 个元素的组合数,记作 C(m,n)C(m,n),公式为: C(m,n)=m!(m−n)!⋅n!C(m,n)=m!(m−n)!⋅n!。
将 mm 个不同的元素分为 kk 组,每组元素的数量为 m1,m2,…mk,(m=m1+m2+…+mk)m1,m2,…mk,(m=m1+m2+…+mk),则不同的分组方式有:
C=C(m,m1)⋅C(m−m1,m2)…C(m−m1−m2−…−m(k−1),mk)C=C(m,m1)⋅C(m−m1,m2)…C(m−m1−m2−…−m(k−1),mk)
⟹C=∏ki−1C(m−∑j−1i−1mi,mj)⟹C=∏i−1kC(m−∑i−1j−1mi,mj)
⟹C=m!m1!⋅m2!…mk!⟹C=m!m1!⋅m2!…mk!
2.古典概率
关于古典概率是以这样的假设为基础的,即随机现象所能发生的事件是有限的、互不相容的,而且每个基本事件发生的可能性相等。
一般说来,如果在全部可能出现的基本事件范围内构成事件A的基本事件有a个,不构成事件A的事件有b个,则出现事件A的概率为 P(A)=aa+bP(A)=aa+b,例如:投掷骰子朝上数字有6种情况,每种情况发生的概率一致,每次点数为1朝上的基本事件有1个,不朝上的事件有5个,那么1朝上的概率为:P(A)=11+5P(A)=11+5
3.联合概率
表示两个事件共同发生的概率,事件A和事件B的共同概率记作:P(AB)、P(A,B)、P(A⋂B)P(AB)、P(A,B)、P(A⋂B),读作“事件A和事件B同时发生的概率”。
4.条件概率
条件概率是指事件A在另外一个事件B已经发生条件下的发生概率。表示为 P(A|B)P(A|B) ,读作“在B条件下A发生的概率”。公式为:
P(A|B)=P(A,B)P(B)P(A|B)=P(A,B)P(B)
一般情况下P(A|B)≠P(A)P(A|B)≠P(A),条件概率有三个特性:
- 非负性
- 可列性
- 可加性
5.全概率公式
若事件A1,A2,…AnA1,A2,…An 构成一个完备事件组且都有正概率,则对任意一个事件B,全概率公式为:
P(B)=∑ni=1P(Ai)P(B|Ai)P(B)=∑i=1nP(Ai)P(B|Ai)
全概率公式的意义在于,当直接计算事件B的概率P(B)P(B) 较为困难时,而 P(Ai),P(B|Ai)(i=1,2,…)P(Ai),P(B|Ai)(i=1,2,…) 的计算较为简单时,可以利用全概率公式计算 P(B)P(B)。思想就是将事件B分割为几个小事件,通过求小事件的概率,然后相加从而求得事件B的概率,而将B事件分割时,不是直接对B进行分割,而是找到样本空间 ΩΩ 的一个个划分 A1,A2,…AnA1,A2,…An 进行分割,分割为 P(B|A1)、P(B|A2)…P(B|An)P(B|A1)、P(B|A2)…P(B|An),然后将各个概率相加。
举例:
例:高射炮向敌机发射三发炮弹,每弹击中与否相互独立且每发炮弹击中的概率均为0.3,又知敌机若中一弹,坠毁的概率为0.2,若中两弹,坠毁的概率为0.6,若中三弹,敌机必坠毁。求敌机坠毁的概率。
解:设事件B=“敌机坠毁”,事件Ai(i=0,1,2,3)。iAi(i=0,1,2,3)。i 是中弹数量 ,那么事件B发生的概率可以分解为 P(B|A0)、P(B|A1)、P(B|A2)、P(B|A3)P(B|A0)、P(B|A1)、P(B|A2)、P(B|A3) 四个概率的和,求解过程:
(1) 求 AiAi 的概率
P(A0)=0.7×0.7×0.7=0.343P(A0)=0.7×0.7×0.7=0.343
P(A1)=(0.3×0.7×0.7)+(0.7×0.3×0.7)+(0.7×0.7×0.3)=0.441P(A1)=(0.3×0.7×0.7)+(0.7×0.3×0.7)+(0.7×0.7×0.3)=0.441
P(A2)=(0.3×0.3×0.7)+(0.3×0.7×0.3)+(0.7×0.3×0.3)=0.189P(A2)=(0.3×0.3×0.7)+(0.3×0.7×0.3)+(0.7×0.3×0.3)=0.189
P(A3)=0.3×0.3×0.3=0.027P(A3)=0.3×0.3×0.3=0.027
(2) 求各个AiAi 发生情况下B发生的概率
P(B|A0)=0.343×0=0P(B|A0)=0.343×0=0
P(B|A1)=0.441×0.2=0.0882P(B|A1)=0.441×0.2=0.0882
P(B|A2)=0.189×0.6=0.1134P(B|A2)=0.189×0.6=0.1134
P(B|A3)=0.027×1=0.027P(B|A3)=0.027×1=0.027
(3) 将各个情况下B发生的概率相加
P(B)=0+0.0882+0.1134+0.027=0.2286P(B)=0+0.0882+0.1134+0.027=0.2286
6.贝叶斯公式
设A1、A2、…AnA1、A2、…An 是样本空间ΩΩ 的一个划分,如果对任意事件B而言,有P(B)>0P(B)>0 那么:
P(Ai|B)=P(BAi)P(B)=P(Ai)⋅P(B|Ai)∑ni=1P(Ai)⋅P(B|Ai)P(Ai|B)=P(BAi)P(B)=P(Ai)⋅P(B|Ai)∑i=1nP(Ai)⋅P(B|Ai)
与全概率公式解决的问题相反,贝叶斯公式是建立在条件概率的基础上寻找事件发生的原因(即大事件B已经发生的条件下,分割中的小事件AiAi 的概率)。
先验概率/边缘概率
P(A)P(A) 在没有数据支持下,A发生的概率,这个概率一般是根据经验估计的。
后验概率
P(A|B)P(A|B) 在已知B发生后A的条件概率。
似然函数
P(B|A)P(B|A) 在已知A发生的情况下的概率分布。
7.期望
期望就是均值,是概率加权下的平均值,是每次可能结果的概率乘以其结果的总和,反应的是随机变量平均取值的大小,也可以理解为预期。
连续型:E(X)=∫∞−∞xf(x)dxE(X)=∫−∞∞xf(x)dx
离散型:E(X)=∑ixipiE(X)=∑ixipi 其中:ii为次数,xixi为第ii 次的取值,pipi 为概率,每次的结果相加,得到期望,也就是预期。
期望的性质:
假设C为一个常数, X和Y是两个随机变量,那么期望有以下性质:
- E(C)=CE(C)=C 常数CC的期望是CC
- E(CX)=CE(X)E(CX)=CE(X) 常数乘以随机变量的期望,可以将常数提出来。
- E(X+Y)=E(X)+E(Y)E(X+Y)=E(X)+E(Y) 两个随机变量的期望等于分别期望加和
- 如果X和Y相互独立,那么E(XY)=E(X)E(Y)E(XY)=E(X)E(Y)
- 如果E(XY)=E(X)E(Y)E(XY)=E(X)E(Y),那么X和Y不相关(但是不一定相互独立)
举例:
AB两个人比赛,假设两个人每一局获胜的概率相等,比赛规则是先胜三局者赢,可以获得100元的奖励,当比赛进行了三局的时候,其中A胜了两居,B胜了一局,这个时候由于某些原因终止了比赛,请问如果分配这100元才比较公平?
解:
(1) 求最终A赢的概率
当第四局A赢,或者第四局输第五局赢时,最终A赢。
P(A)=P(赢|4)+P(赢|5,输|4)=12+12×12=34P(A)=P(赢|4)+P(赢|5,输|4)=12+12×12=34
(2) 求最终B赢的概率
当第四局、第五局都赢时,最终B赢。
P(B)=P(赢|4)×P(赢|5)=12×12=14P(B)=P(赢|4)×P(赢|5)=12×12=14
(3) 加权平均后分配100元
E(A)=100×P(A)=100×34=75E(A)=100×P(A)=100×34=75
E(B)=100×P(B)=100×14=25E(B)=100×P(B)=100×14=25
8.方差
方差是衡量随机变量或一组数据离散程度的度量,是用来度量随机变量和其数学期望之间的偏离程度。方差描述的是数据的离散程度。
公式为:
Var(X)=D(X)=σ2=∑(X−μ)2NVar(X)=D(X)=σ2=∑(X−μ)2N
离散型:D(X)=∑ni=0pi⋅(xi−μ)2D(X)=∑i=0npi⋅(xi−μ)2
连续型:D(X)=∫ba(x−μ)2f(x)dxD(X)=∫ab(x−μ)2f(x)dx
方差可以用期望进行计算:
D(X)=E((X−E(X))2)=E(X2)−(E(X))2D(X)=E((X−E(X))2)=E(X2)−(E(X))2
方差的性质:
假设C为一个常数,X和Y是两个随机变量,那么方差有以下性质:
- D(C)=0D(C)=0 常数的方差是0
- D(CX)=C2D(X)D(CX)=C2D(X)
- D(C+X)=D(X)D(C+X)=D(X)
- D(X±Y)=D(X)+D(Y)±2Cov(X,Y)D(X±Y)=D(X)+D(Y)±2Cov(X,Y)
- 如果X和Y不相关,那么D(X±Y)=D(X)+D(Y)D(X±Y)=D(X)+D(Y)
9.标准差
标准差是方差的算术平方根,是离均值平方的算术平均数的平方根,用符号σσ表示。
标准差和方差都是测量离散趋势的最重要,最常见的指标,标准差和方差的不同点在于,标准差和变量的计算单位是相同的,比方差清楚,因此在很多分析的时候使用的是标准差。
方差的公式:
σ=D(X)−−−−−√=∑(x−μ)2N−−−−−−−−−√σ=D(X)=∑(x−μ)2N
10.协方差
协方差常用于衡量两个变量的总体误差,当两个变量相同的情况下,协方差其实就是方差。
如果X和Y是独立统计的,那么二者之间的协方差为0。
Cov(X,Y)Cov(X,Y)
=E[(X−E(X))⋅(Y−E(Y))]=E[(X−E(X))⋅(Y−E(Y))]
=E[XY−XE(Y)−YE(X)+E(X)E(Y)]=E[XY−XE(Y)−YE(X)+E(X)E(Y)]
=E{(X−E(X))⋅(Y−E(Y))}=E{(X−E(X))⋅(Y−E(Y))}
协方差矩阵
对于n个随机向量(X1,X2,X3,…XnX1,X2,X3,…Xn),任意两个元素XiXi和XjXj都可以得到一个协方差,从而形成一个n∗nn∗n的矩阵,该矩阵就是协方差矩阵。协方差矩阵是对称矩阵。
11.相关系数
协方差可以描述X和Y的相关程度。
可以引入相关系数来表示X和Y的相关性。
相关系数可以用公式表示为:
σ=Cov(X,Y)D(x)−−−−√⋅D(Y)−−−−−√σ=Cov(X,Y)D(x)⋅D(Y)
当p(X,Y)=0时,称X和Y不线性相关。
相关系数的取值范围为[-1,1]
12.峰度
峰度又称为峰态系数,表示了概率密度分布曲线在平均值处峰值高低的特征数,直观来讲,峰度反映的是锋部的尖度。
样本的峰度是和正态分布相比较而言的统计量,如果峰度值大于3(正态分布的峰度是3),那么峰的形状比较尖,比正态分布峰要陡峭。
峰度计算公式:随机变量的四阶中心矩与方差平方的比值。
kurtosis=∑Ni=1(xi−x¯¯¯)4(N−1)⋅s4kurtosis=∑i=1N(xi−x¯)4(N−1)⋅s4
13.偏度
偏度系数是描述分布偏离对称性程度的一个特征数,当分布左右对称的时候,偏度系数为0,当偏度系统数大于0时候,即重尾在右侧时候,该分布为右偏,当偏度系数小于0的时候,即重尾在左侧的时候,该分布为左偏。
偏度计算公式:随机变量的三阶中心距与样本的平均离均差立方和的比值。
kurtosis=∑Ni=1(xi−x¯¯¯)3(N−1)⋅s3kurtosis=∑i=1N(xi−x¯)3(N−1)⋅s3
14.概率密度函数
概率密度函数是一个描述随机变量的输出值,在某个确定的取值点附近的可能性的函数。
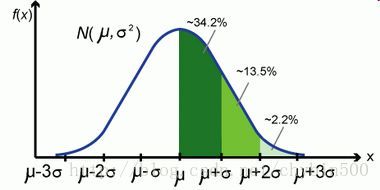
15.正态分布
正态分布(Normal Distribution)又称为常态分布、高斯分布。
若随机变量X服从一个数学期望为μμ,方差为σ2σ2,那么认为随机变量X服从正态分布,记作N(μ,σ2)N(μ,σ2)
标准正态分布
正态分布的概率密度函数由正态分布的期望值μμ 决定其位置,其标准差σ2σ2 决定了分布的幅度,当σ=1,μ=0σ=1,μ=0时正态分布为标准正态分布。
正态分布的概率密度函数
f(x)=1σ2π−−√⋅e−(x−μ2)2σ2f(x)=1σ2π⋅e−(x−μ2)2σ2
正态分布的特点
- 值域:(−∞,+∞)(−∞,+∞)
- 期望:μμ
- 峰度:3
- 方差:σ2σ2
- 中位数:μμ
- 众数:μμ
- 偏度:0
16.两点分布(0-1分布、伯努利分布)
分布结果只有1或者0,这种分布是0-1分布,两种分布的概率和为1。
P(X=1)+P(X=0)=1P(X=1)+P(X=0)=1
期望
E(X)=1∗p+0∗q=pE(X)=1∗p+0∗q=p
方差
D(X)=E(X2)−[E(X)]2=12∗p+02∗(1−p)−p2=pqD(X)=E(X2)−[E(X)]2=12∗p+02∗(1−p)−p2=pq
17.二项分布
二项分布就是重复n次独立的伯努利试验。在每次试验中只有两种可能的结果,而且两种结果发生与否互相对立,并且相互独立,与其它各次试验结果无关,事件发生与否的概率在每一次独立试验中都保持不变,则这一系列试验总称为n重伯努利实验,当试验次数为1时,二项分布服从0-1分布。
重复n次的伯努利试验(Bernoulli Experiment),用ξξ表示随机试验的结果。如果事件发生的概率是P,则不发生的概率q=1-p,N次独立重复试验中发生K次的概率是
P(ξ=K)=Cknpk∗qn−kP(ξ=K)=Cnkpk∗qn−k
二项式分布的期望:E(ξ)=npE(ξ)=np
二项式分布的方差:D(ξ)=npqD(ξ)=npq
18.几何分布
几何分布是指在n次伯努利实验中,实验k次才得到第一次成功的几率,其中前k-1次实验均失败,第k次实验成功。
如果事件发生的概率为p,不发生的概率为q,则第k次事件成功的概率为:
P(ξ=k)=qk−1∗pP(ξ=k)=qk−1∗p
几何分布期望为:E(ξ)=1pE(ξ)=1p
几何分布的方差为:D(ξ)=1−pp2D(ξ)=1−pp2
19.泊松分布
泊松分布常用于描述单位时间内随机事件发生的次数,使用参数λλ 表示单位时间(或者单位面积)内随机事件的平均发生率。
当二项分布的n很大,而p很小的时候,泊松分布可以看做是二项式分布的近似,一般当n>20,p<0.05n>20,p<0.05 的时候就可以近似计算了。
泊松分布的函数是:
P(X=k)=λkk!⋅e−λ,k=0,1,2…,λ>0P(X=k)=λkk!⋅e−λ,k=0,1,2…,λ>0
泊松分布的期望和方差均为 λλ。
20.平均分布
均匀分布也叫矩形分布,它是对称概率分布,在相同长度间隔的分布概率是等可能的。
概率密度函数
f(x)={1b−a,0,a<x<bx取其他值f(x)={1b−a,a<x<b0,x取其他值
期望
E(x)=∫+∞−∞xf(x)dx=∫ba1b−axdx=1b−a⋅12⋅(b2−b2)=12(a+b)E(x)=∫−∞+∞xf(x)dx=∫ab1b−axdx=1b−a⋅12⋅(b2−b2)=12(a+b)
方差
(b−a)3=(b−a)(b2−2ab+a2)(b−a)3=(b−a)(b2−2ab+a2)
E(x2)=∫bax21b−adx−(a+b2)2=(b−a)212E(x2)=∫abx21b−adx−(a+b2)2=(b−a)212
21.指数分布
指数分布是一种连续概率分布,常用来表示独立随机事件发生的时间间隔,比如旅客进机场的时间间隔,用户下订单的时间间隔。
指数分布是可靠性研究中最常用的一种分布形式。
λλ 是分布的一个参数,被称为率参数,即每单位时间内发生某事件的次数,指数分布的区间是[0,+∞][0,+∞]。
概率密度函数
f(x)={λe−λx,x>00,x≤0,其中λ>0f(x)={λe−λx,x>00,x≤0,其中λ>0
期望
E(X)=∫∞−∞xf(x)dx=−xe−λx|∞0+∫+∞0e−λxdx=−1λ∫∞0e−λxd(−λx)=1λE(X)=∫−∞∞xf(x)dx=−xe−λx|0∞+∫0+∞e−λxdx=−1λ∫0∞e−λxd(−λx)=1λ
方差
D(x)=1λ2D(x)=1λ2
22.切比雪夫不等式
设随机变量X的期望是μμ,方差是σ2σ2,对于任意的正数ξξ,有以下不等式成立。
P{|X−μ|≥ξ}≤σ2ξ2P{|X−μ|≥ξ}≤σ2ξ2
切比雪夫不等式的含义是:方差D(X)越小,事件{|X−μ|<ξ}{|X−μ|<ξ} 发生的概率就越大,即:X取值基本上都集中在期望值μμ附近。
23.大数定律
设随机变量X1、X2、X3、…,XnX1、X2、X3、…,Xn 是一列相互独立的随机变量( 两两不相关),并且分别存在期望E(Xk)E(Xk) 和方差 D(Xk)D(Xk) ,对于任意小的正数ξξ,有
limn→∞P{|1n∑k=1nXk−1n∑k=1nE(xk)|<ξ}=1limn→∞P{|1n∑k=1nXk−1n∑k=1nE(xk)|<ξ}=1
当具有相同的期望μμ 和方差σ2σ2 的时候,对随机变量的均值Yn=1n∑ni=1XiYn=1n∑i=1nXi ,则有 limn→∞P{|Yn−μ|<ξ}=1limn→∞P{|Yn−μ|<ξ}=1
大数定理的意义
随着样本容量的n的增加,样本平均数将接近与总体平均数(期望μμ),所以在统计推断中,一般都会使用样本平均数估计总体平均数的值。也就是说我们会使用一部分样本的平均值来代替整体样本的期望,当n足够大的时候,偏差的可能性是非常小的,当n无限大的时候,这种有偏差的可能性的概率基本为0。
24.中心极限定理
独立同分布
在概率统计理论中,指随机过程中,任何时刻的取值都为随机变量,如果这些随机变量服从同一分布,并且互相独立,那么这些随机变量是独立同分布。
假设{Xn}{Xn} 为独立同分布的随机变量序列,并具有相同的期望μμ 和方差 σ2σ2 ,则 {Xn}{Xn} 服从中心极限定理,切 ZnZn 为随机序列{Xn}{Xn} 的规范和。
Yn=X1+X2+X3+…+Xn=∑i=1nXiYn=X1+X2+X3+…+Xn=∑i=1nXi
Zn=Yn−E(Yn)D(Yn)−−−−−√=Yn−nμn−−√μ→N(0,1)Zn=Yn−E(Yn)D(Yn)=Yn−nμnμ→N(0,1)
YnYn 是各个样本的累加和,而规范和ZnZn 就是累加和减去期望,然后除以标准差。当n很大的时候,就趋近于标准正态分布N(0,1)N(0,1)
中心极限定理的意义
一般在同分布的情况下,抽样样本值的和在总体数量趋于无穷时的极限分布近似于正态分布N(μ,σ2)N(μ,σ2)。
25.最大似然法
似然
根据结果预测参数。
概率
根据参数预测结果
最大似然是参数估计的一个方法。
基本思想
当从模型总体随机抽取n组样本观测后,最合理的参数估计量应该使得从模型中抽取该n组样本观测值的概率最大。
最大似然法估计值的一般步骤
(1) 写出似然函数
(2)对似然函数取对数,并整理
(3)求导数
(4)解似然方程
26.状态转移模型
某随机过程ππ ,他的状态有nn 个,当前时间tt时位于ii状态,它在t+1t+1 时刻位于jj 状态的概率为P(i,j)=P(j|i)P(i,j)=P(j|i)。
意思就是状态转移的概率只依赖上一个状态值。
π(Xn+1=j)=∑i=1Kπ(Xn=i)⋅P(Xn+1=j|Xn=i)π(Xn+1=j)=∑i=1Kπ(Xn=i)⋅P(Xn+1=j|Xn=i)
⟹πn+1=πn⋅P⟹πn+1=πn⋅P
这个公式表示第n+1n+1为j的概率是,KK种情况下分别可以状态转移到jj 的概率相加,也就是πnπn 乘以状态转移矩阵P。
扫码向博主提问
![]()
鸣宇淳
博客专家
非学,无以致疑;非问,无以广识