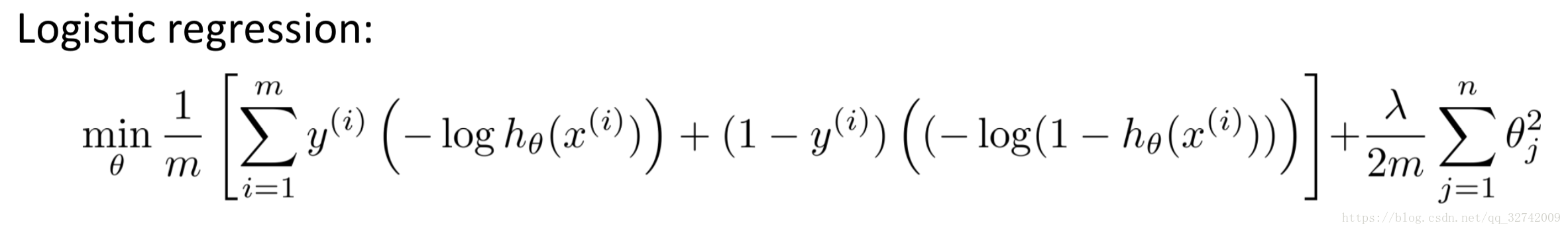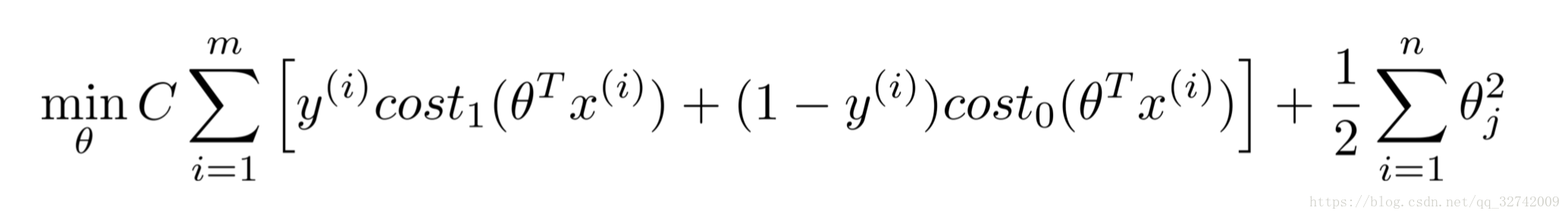Hinge Loss 解释
SVM 求解使通过建立二次规划原始问题,引入拉格朗日乘子法,然后转换成对偶的形式去求解,这是一种理论非常充实的解法。这里换一种角度来思考,在机器学习领域,一般的做法是经验风险最小化 (empirical risk minimization,ERM),即构建假设函数(Hypothesis)为输入输出间的映射,然后采用损失函数来衡量模型的优劣。求得使损失最小化的模型即为最优的假设函数,采用不同的损失函数也会得到不同的机器学习算法,比如这里的主题 SVM 采用的是 Hinge Loss ,Logistic Regression 采用的则是负 Logistic 损失。
从二项分布的角度来考虑 Logistic 回归:
这里另 ,
为 sigmoid 映射,则:
的图形如下图的红色曲线,可见
,
的取值越小,即损失越小。反之另:
此时得到的图像应该为关于 对称的红色的线(没画出),此时
,
的取值越小,即损失越小。

注: 图中绿色的线为 Square Loss ,蓝色的线为 Hinge Loss, 红的的线为负 Logistic 损失,黑色的线为0-1损失。
二分类问题
给定数据集 , 要用这些数据做一个线性分类器,即求得最优分离超平面
来将样本分为正负两类,给定数据集后只需求得最优的参数
即可,为了解决这个问题,首先做出如下线性映射函数
根据经验风险最小化原则, 这里引入二分类的 Hinge Loss :
上图中对应的 ,所以SVM可以通过直接最小化如下损失函数二求得最优的分离超平面:
相当于一个L2正则项。
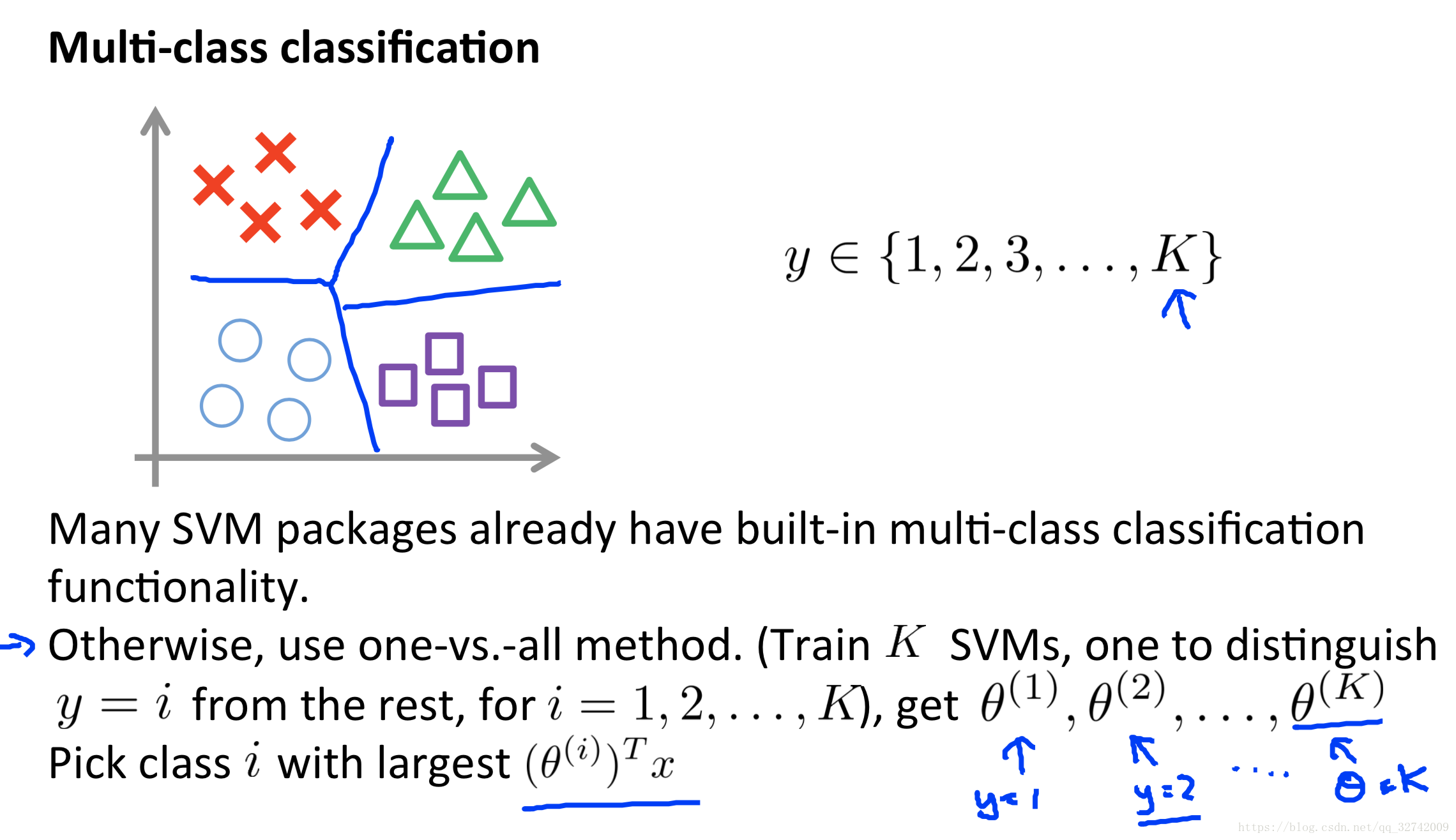
多分类问题
对于多分类问题依旧使用的是One VS All策略
从LR到SVM
接下来将重点讲LR与SVM损失函数之间的关系,参考Andrew NG教授的课件。
在下面的推导中标签被分为两类,非0即1.
support vector machine:
观察可以发现,两者极为相似。SVM在LR之上做了两处改动:
- SVM对整体损失乘了样本数(m),并将正则化因子
移到了前头,改成了C(
).
- SVM将损失函数由对数损失函数改成了Hinge Loss.其中
,
对上面的式子稍微做一些变化即可推导回我们所熟悉的形式。
,将偏差b从参数中分离出来,并记
(表示
中除去第一个元素之外的所有元素)且记
。
则有
同理,有
为方便定义函数间隔,将负类的标签改为-1;
则综合上面两个条件,有
此时都为0,化简目标函数可得
好了,这就和我们之前优化求解二次规划问题的形式一模一样了!
SVM核函数(SVM with Kernels)
之前已经有写过核函数了,但那边着重介绍的是核函数可以被方便的用在svm中从而解决非线性可分问题,以及一些优点。但是对于核函数到底做了一件什么事情可能还是一知半解,说白了就是映射。
重新再回顾一遍吴恩达的教案。
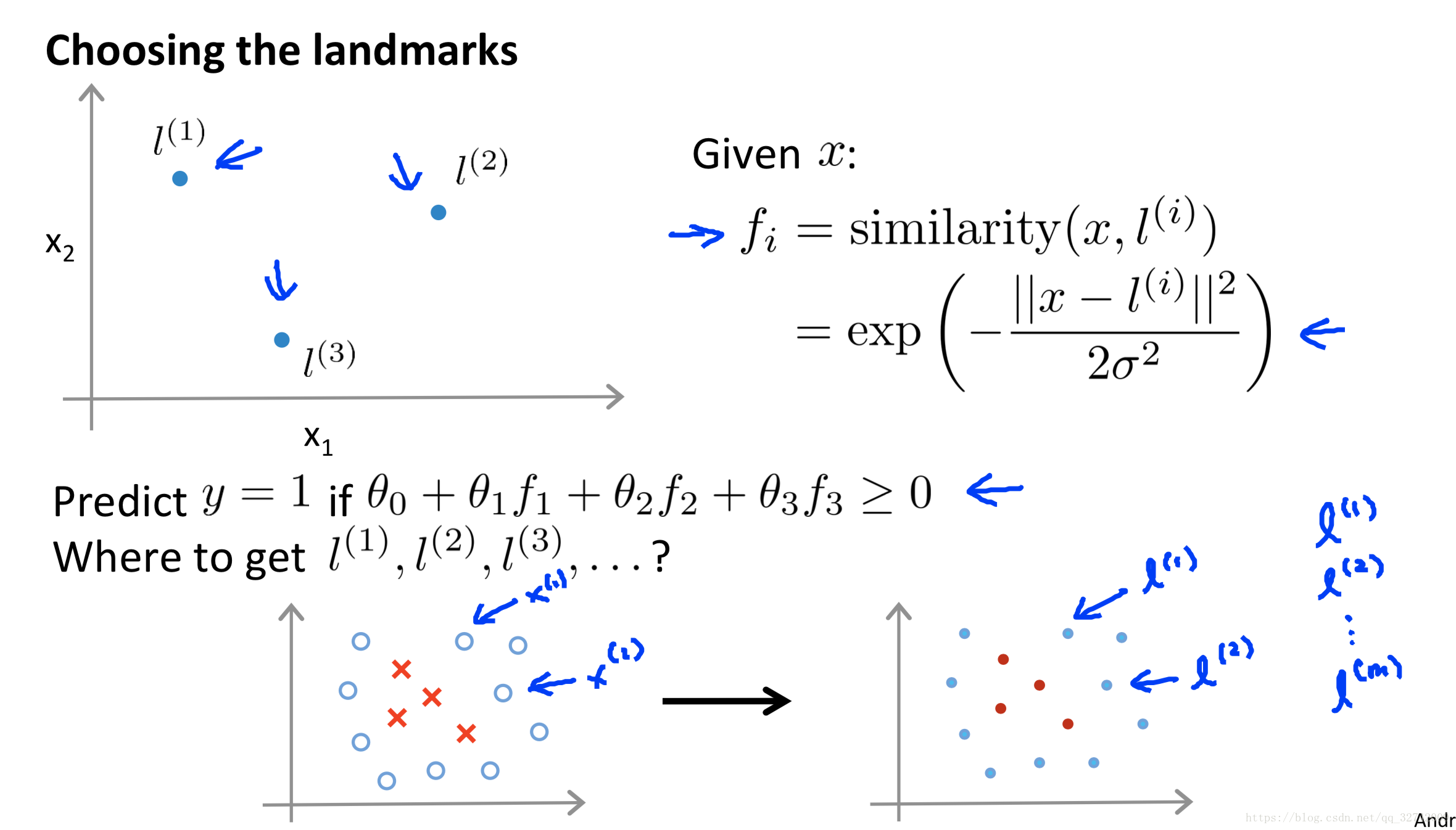
要解决非线性问题,就需要引入组合特征,将原问题映射到高维空间中去。这边引入了新的特征f以代替原先的特征,以拥有非线性的决策边界。但是这里有很明显的缺点,手动构建特征很明显是无法适应问题的。
以高斯核为例,我们把每个样本点自身作为一个landmark,将样本点与每个landmark之间的相似度(类似于距离)作为新的特征。
上图很明显的说明了,当x靠近的时候,特征趋近于1,很远的话就为0了。
其实很容易理解,当新的样本点靠近正样本的时候,正样本的权重比较大,则新的样本有更大的可能被归为正样本。
吴恩达的教案中是从实例的角度讲解了高斯核的用法。
下一篇讲一下用SVM回归,之后有时间再研究一下SMO算法