题目描述
给你 组询问,对于每组询问给出正整数 ,求将 拆分成 个正整数相加的形式的方案数,且这 个正整数的最大公约数为 。答案对 取模。
数据范围
分析
PART 1 一个询问
第一眼看这个题目,如果只有1个询问而不是 这个询问,那我们可以用类似D题的做法,我们设 表示将 拆分成 个正整数相加的形式,且这 个正整数 为 的方案数,那么容易得到 。至于这个是怎么来的呢?
首先一定有 ,那么我们可以把 分为 块,每块大小为 。(如下图)
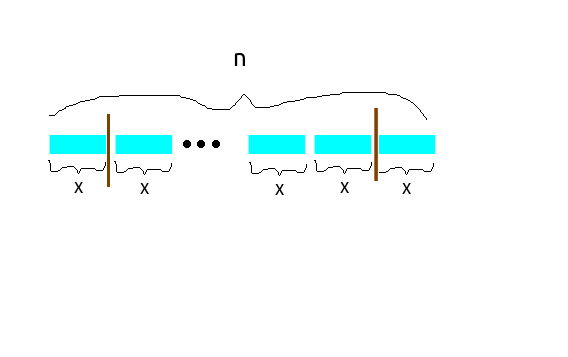
那么问题就相当于是在这 个空隙中插入 个隔板,这样保证分出来的 个数的 一定是至少为 ;但是,不一定是所有的的分法得到的 都恰好是 ,也可能是 ,因此,我们要除去这些情况,也就是说,减去分出得到的 是 的情况,这样就得到了上面的式子。
(怎么样,这个口糊容斥是不是很完美?好吧我并不会用
和
的方法去证)
PART 2 Q个询问
然而题目不总是那么友好。题目给出
个询问,更过分的是
居然到了
!
如果我们每次询问都这样暴力做的话显然会超时,那怎么办呢?考虑到我们计算的时候肯能会有一些冗余的重复计算,这时候我们就会自然而然地想到一个叫做记忆化的东西。首先,我们刚刚的式子中只涉及到了一个状态,那是因为我们在给定
和
的情况下。现在我们加入
和
,可以表示出一个三维的状态,设
表示把
分成
份,
为
的方案数,则仍然有
。我们要求的就是
,则有
。但是这样的话我们还需要计算这个
,这其实就是前面提到的问题,但是我们又去计算
,这样的话并没有减少冗余的计算。那么我们有什么方法来优化一下呢?我们再看一看上面的图,可以得到这样一个神奇的式子:
。这个可以直接从状态表示的意义上利用最大公约数的一个性质(
)证明。或者说,(对于上面的图)我们把
分成大小为
的
块之后,为了保证这个
仍然为
,那么我们就不能让这
块分出来得到的
大于
,用反证法,若这个分块后
大于
,那么可知原来的
一定大于
。
这样,我们就可以省去最后一维,直接用
表示把
拆分成
个正整数相加,且
为
的方案数。当然,如果我们预处理出这个
数组,时间和空间都是不允许的,因此我们只能在线处理。当然了,我们不能直接开这个
数组,这时候我们就可以用一个叫
的好东西,然后用一个
表示一下
和
的状态即可。
参考程序
// Codeforces 439 E
// Round #251 (Div. 2)
#pragma GCC optimize(3) // 这些优化开关是给map准备的,不知道去了可不可以过,应该去掉也是不会T的
#pragma GCC optimize("Ofast")
#pragma GCC optimize("inline")
#pragma GCC optimize("-fgcse")
#pragma GCC optimize("-fgcse-lm")
#pragma GCC optimize("-fipa-sra")
#pragma GCC optimize("-ftree-pre")
#pragma GCC optimize("-ftree-vrp")
#pragma GCC optimize("-fpeephole2")
#pragma GCC optimize("-ffast-math")
#pragma GCC optimize("-fsched-spec")
#pragma GCC optimize("unroll-loops")
#pragma GCC optimize("-falign-jumps")
#pragma GCC optimize("-falign-loops")
#pragma GCC optimize("-falign-labels")
#pragma GCC optimize("-fdevirtualize")
#pragma GCC optimize("-fcaller-saves")
#pragma GCC optimize("-fcrossjumping")
#pragma GCC optimize("-fthread-jumps")
#pragma GCC optimize("-funroll-loops")
#pragma GCC optimize("-fwhole-program")
#pragma GCC optimize("-freorder-blocks")
#pragma GCC optimize("-fschedule-insns")
#pragma GCC optimize("inline-functions")
#pragma GCC optimize("-ftree-tail-merge")
#pragma GCC optimize("-fschedule-insns2")
#pragma GCC optimize("-fstrict-aliasing")
#pragma GCC optimize("-fstrict-overflow")
#pragma GCC optimize("-falign-functions")
#pragma GCC optimize("-fcse-skip-blocks")
#pragma GCC optimize("-fcse-follow-jumps")
#pragma GCC optimize("-fsched-interblock")
#pragma GCC optimize("-fpartial-inlining")
#pragma GCC optimize("no-stack-protector")
#pragma GCC optimize("-freorder-functions")
#pragma GCC optimize("-findirect-inlining")
#pragma GCC optimize("-fhoist-adjacent-loads")
#pragma GCC optimize("-frerun-cse-after-loop")
#pragma GCC optimize("inline-small-functions")
#pragma GCC optimize("-finline-small-functions")
#pragma GCC optimize("-ftree-switch-conversion")
#pragma GCC optimize("-foptimize-sibling-calls")
#pragma GCC optimize("-fexpensive-optimizations")
#pragma GCC optimize("-funsafe-loop-optimizations")
#pragma GCC optimize("inline-functions-called-once")
#pragma GCC optimize("-fdelete-null-pointer-checks")
#include <cstdio>
#include <utility>
#include <map>
#define fir first
#define sec second
typedef long long LL;
typedef std::pair<int, int> P;
typedef std::map<P, int> Arr;
const int MAXN = 100005;
const int MOD = 1000000007;
int inv[MAXN], fac[MAXN];
Arr DP;
int pow(int bs, int ex) { // 快速幂
int res = 1;
for (; ex; ex >>= 1, bs = (LL)bs * bs % MOD) if (ex & 1) res = (LL)res * bs % MOD;
return res;
}
inline void subtrac(int & x, int d) { x = x + MOD - d; while (x >= MOD) x -= MOD; }
inline int C(int n, int r) { return (LL)fac[n] * inv[r] % MOD * inv[n - r] % MOD; } // 算组合数
void init();
int dp(P);
namespace FastIO {
template <typename T>
void read(T & x) {
x = 0; register char ch = getchar();
for (; ch < '0' || ch > '9'; ch = getchar());
for (; ch >= '0' && ch <= '9'; x = (x << 3) + (x << 1) + (ch ^ '0'), ch = getchar());
}
template <typename T>
void write(T x) {
if (!x) return (void)(putchar('0'));
register int arr[15], len = 0;
for (; x; arr[len++] = x % 10, x /= 10);
while (len) putchar(arr[--len] ^ '0');
}
template <typename T>
inline void writeln(T x) {
write(x), putchar('\n');
}
}
int main() {
init();
int Q, n, f;
using FastIO::read;
read(Q);
for (int i = 0; i < Q; i++) {
read(n), read(f);
FastIO::writeln(dp(P(n, f)));
}
return 0;
}
void init() { // 预处理1e5以内的阶乘极其逆元
int i, j, k;
for (fac[0] = i = 1; i <= 100000; i++) fac[i] = (LL)i * fac[i - 1] % MOD;
inv[100000] = pow(fac[100000], MOD - 2);
for (i = 99999; i >= 0; --i) inv[i] = (LL)(i + 1) * inv[i + 1] % MOD;
}
// 核心部分就这么一点点
int dp(P now) {
if (DP.find(now) != DP.end()) return DP[now];
if (now.sec == 1 && now.fir > 1 || now.sec > now.fir) return 0; // 这里要特别注意,不合法的状态直接返回0即可,不要再存入map,否则非常耗时间,会TLE,一开始就是因为这个T了半天
int & res = DP[now];
res = C(now.fir - 1, now.sec - 1);
for (int k = 2; (LL)k * k <= now.fir; k++)
if (!(now.fir % k)) {
subtrac(res, dp(P(now.fir / k, now.sec)));
if (k * k != now.fir) subtrac(res, dp(P(k, now.sec)));
}
return res;
}总结
这题如果没有那 个询问,其实并不难。加上询问之后的重点主要在于对冗余计算的处理,再把之前对一个询问的做法变成加上 和 两维,最后最最重要的地方在于省去 那一维的变形,那个变式若推出来了,整到题也就做完了。
附 更加数学性的做法
其实上述做法为口糊容斥,不过挺好…
那么我们应该怎么像之前一样用
和
的方式去推理呢?
以下内容来自Codeforces
类似于上面的DP方程,令 表示将正整数 分成 份, 为 的方案数;令 为把 分成 个正整数相加的形式的方案数,即 。那么有 ,又由 ,移项得 。其实这个式子我们通过刚刚对DP转移方程的推理也是可以得到的,不过我们要把这个式子反演过来并不能用我们以前的方法———它不含有那些组合数。事实上呢,这个要用到数论里的一个反演技巧——莫比乌斯反演。
就是这样的如果两个函数满足:
那么有在这里 即 , 即 。