AtCoder Regular Contest 082 (Upc 6603) ConvexScore

题目链接：https://arc082.contest.atcoder.jp/tasks/arc082_c

Problem Statement

You are given N points (xi,yi) located on a two-dimensional plane. Consider a subset S of the N points that forms a convex polygon. Here, we say a set of points Sforms a convex polygon when there exists a convex polygon with a positive area that has the same set of vertices as S. All the interior angles of the polygon must be strictly less than 180°.

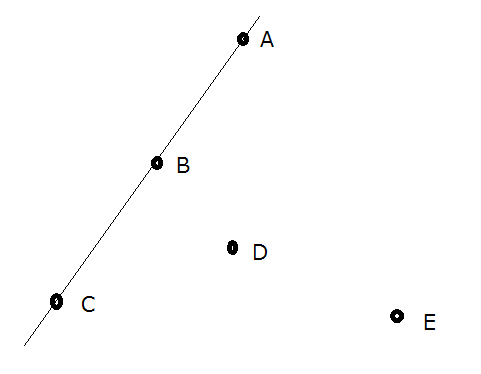
For example, in the figure above, {A,C,E} and {B,D,E} form convex polygons; {A,C,D,E}, {A,B,C,E}, {A,B,C}, {D,E} and {} do not.

For a given set S, let n be the number of the points among the N points that are inside the convex hull of S (including the boundary and vertices). Then, we will define the score of S as 2n−|S|.

Compute the scores of all possible sets S that form convex polygons, and find the sum of all those scores.

However, since the sum can be extremely large, print the sum modulo 998244353.

Constraints

• 1≤N≤200
• 0≤xi,yi<104(1≤i≤N)
• If i≠j, xi≠xj or yi≠yj.
• xi and yi are integers.

---

Input

The input is given from Standard Input in the following format:

N
x1 y1
x2 y2
:
xN yN

Output

Print the sum of all the scores modulo 998244353.

---

Sample Input 1

Copy

4
0 0
0 1
1 0
1 1

Sample Output 1

Copy

5

We have five possible sets as S, four sets that form triangles and one set that forms a square. Each of them has a score of 20=1, so the answer is 5.

---

Sample Input 2

Copy

5
0 0
0 1
0 2
0 3
1 1

Sample Output 2

Copy

11

We have three "triangles" with a score of 1 each, two "triangles" with a score of 2 each, and one "triangle" with a score of 4. Thus, the answer is 11.

---

Sample Input 3

Copy

1
3141 2718

Sample Output 3

Copy

0

There are no possible set as S, so the answer is 0.

题意：阅读理解，鉴定完毕，自爆。

平面上有n(n<=200）个点，对于其中能够构成凸多边形的点集S，计算一个得分score，并输出所有这样能构成凸多边形的点集的得分之和sigma(score)。score=2^(n-|S|), n: 构成此凸多边形的点数及其内部的点数总和;|S|: 构成此凸多边形的点数（外边的罗阔的哪些点）。 
题目要求的score，对于一个凸多边形点集S来说，就是在已经选择了此凸多边形的情况下，里面的点任意选择的方案数； 
即以此凸多边形为凸包的点集的总方案数； 
而对于整道题目来说，就是给出n个点，求它们所能构成凸包的方案总数。
逆向思维： 
n个点一共有2^n个点集（好吧包括空集C(n,0)==1、单点集C(n,1)==1和必然共线的两点集C(n,2)…,无妨，稍后会在计算中减去它们),从这2^n个总方案里面减去不能构成凸包的方案数，即可更轻松地得到答案。因不能构成凸包的方案数很少，空集、单点、两点以及多个共线的点的时候。而求多点共线的方案就比较简单了：for/for/for，3层for循环大概8*10^6的复杂度，外层2道循环枚举不同的两点i,j，内循环枚举落在被i,j确定的那条直线上面的点，构成的点集有多少个点，则减去它们造成的不能构成凸包的方案数即可。注意细节。

（题意贴的别人的，我怕自己说的不好）

#include<bits/stdc++.h>
using namespace std;
const long long mod = 998244353;
struct node{
	int x;
	int y;
}no[205];
long long Qpow(long long x,int n)
{
	long long ans=1;
	while(n)
	{
		if(n&1)
			ans=(ans*x)%mod;
		x=(x*x)%mod;
		n=n>>1;
	}
	return ans;
}
int main()
{
	int n;
	scanf("%d",&n);
	long long ans=Qpow(2,n)-1-n;
	for(int i=0;i<n;i++)
		scanf("%d%d",&no[i].x,&no[i].y);
	for(int i=0;i<n;i++)
	{
		for(int j=i+1;j<n;j++)
		{
			int sum=0;
			for(int k=j+1;k<n;k++)
				if ((no[j].x-no[i].x) * (no[k].y-no[j].y) == (no[k].x-no[j].x) * (no[j].y-no[i].y)) 
					sum++;
			ans=(ans-Qpow(2,sum)+mod)%mod;
		}	
	}	
	printf("%lld\n",ans%mod); 
	return 0;
}