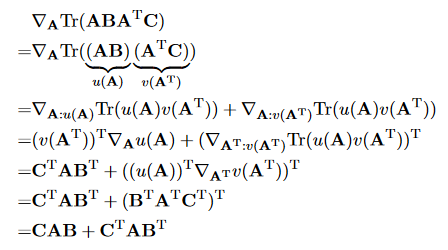矩阵
为转置
表示n阶单位阵
对于n阶方阵A,它的迹是主对角线上的元素之和,即,有如下性质:
n阶方阵行列式定义为:,其中Sn为所有n阶排列的集合,
的值为-1或+1取决于
为奇排列或者偶排列,即其中出现的降序的次数为奇数或者偶数,例如(1,3,2)中降序次数为1,(3,1,2)中降序次数为2。
n阶方阵的行列式有如下性质:
矩阵A的Frobenius范数定义为:
可以看出,矩阵的Frobenius范数就是将矩阵扩张成向量后的L2范数。
导数
向量a,对于标量x的导数,以及x相对于a的导数都是向量,第i个分量分别为:
类似的,矩阵A对于标量x的导数,以及x对于A的导数都是矩阵,其第i行j列的元素为:
对于函数f(x),假定其对向量的元素可到,则f(x)关于x的一阶导数是一个向量,其第i个分量为:
f(x)关于x的二阶导数是称为海森矩阵(Hessian matrix)的一个方阵,其第i行第j列上的元素为:
向量和矩阵的导数满足乘法法则
由和上式可知:
证明过程见:逆矩阵求导
若求导的标量是矩阵A的元素,则有
,证明过程如下:参考:方阵的迹(trace)及其微分(导数)
SVD
任意实矩阵A都可以分解为:
U和V 分别满足和
。
,且其他位置元素均为0,
U中的列向量称为A的左奇异向量,V中的列向量称为A的右奇异向量, 是奇异值,矩阵A的秩等于非0奇异值的个数。